Kreisgruppe

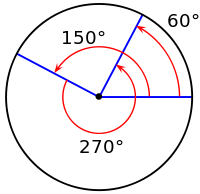
Die Hintereinanderausführung von Drehungen entspricht der Addition von Winkeln, hier: 150° + 270° = 420° = 60°

Die Kreisgruppe $\mathbb {S}$ oder Torusgruppe $\mathbb{T}$ ist in der Mathematik eine Gruppe, die die Drehungen um einen festen Punkt im zweidimensionalen Raum (einer Ebene) zusammenfasst und die Hintereinanderausführung dieser Drehungen beschreibt. Eine solche Drehung lässt sich eindeutig durch einen Winkel beschreiben, die Hintereinanderausführung zweier Drehungen entspricht gerade der Drehung um die Summe der beiden Winkel der einzelnen Drehungen. Eine volle Umdrehung wird dabei wiederum mit keiner Drehung identifiziert.

Definition über Winkel

Ausgehend von der Vorstellung als Gruppe der Winkel mit Addition, lässt sich die Kreisgruppe als Faktorgruppe ${\mathbb {S}}:=\mathbb{R} /\mathbb{Z }$ definieren, das heißt, je zwei Elemente, die sich um eine ganze Zahl unterscheiden (in der Anschauung eine ganzzahlige Anzahl voller Umdrehungen), werden miteinander identifiziert. Möchte man einen direkten Bezug zu Winkelangaben im Bogenmaß ziehen, ist ebenso die Definition ${\mathbb {S}}:=\mathbb{R} /(2\pi \mathbb{Z } )$ möglich.

Beispiel: Stellt man die Elemente der Kreisgruppe durch Repräsentanten dar, etwa als reelle Zahlen zwischen null (einschließlich) und eins (ausschließlich), so ergibt sich beispielsweise:

$0{,}3+0{,}4=0{,}7\,,\quad 0{,}3+0{,}8=0{,}1\,,\quad 0{,}4+0{,}6=0{,}0$ (der Vorkommateil entfällt).

Diese Konstruktion ist möglich, da $\mathbb {Z}$ – wie jede Untergruppe, da $\mathbb {R}$ abelsch ist – ein Normalteiler von $\mathbb {R}$ ist. Da $\mathbb {Z}$ zudem abgeschlossen ist, ist $\mathbb{R} /\mathbb{Z }$ auch wiederum eine topologische Gruppe, die Eigenschaften wie die Lokalkompaktheit und Metrisierbarkeit von $\mathbb {R}$ erbt.

Als Lie-Gruppe

Die Kreisgruppe lässt sich äquivalent als spezielle orthogonale Gruppe SO(2) definieren, d.h. als Menge der reellen Matrizen der Form

${\begin{pmatrix}a&b\\-b&a\end{pmatrix}}$ ,

für die $a^{2}+b^{2}=1$ gilt, mit der Matrizenmultiplikation als Gruppenverknüpfung. Dies sind gerade die Drehmatrizen im zweidimensionalen Raum ( SO(n) im -dimensionalen Raum). Mittels der Koordinaten (a,b) lässt sich jedes solches Gruppenelement als Punkt auf dem Einheitskreis in der zweidimensionalen Ebene auffassen – die Bedingung $a^{2}+b^{2}=1$ besagt gerade, dass (a,b) auf diesem Kreis liegt. Der Kreis – auch genannt 1-Sphäre – bildet eine eindimensionale differenzierbare Mannigfaltigkeit, wie bei jeder solchen Matrix-Gruppe ist die Verknüpfung mit der Struktur der Mannigfaltigkeit kompatibel, daher bildet die Kreisgruppe eine Lie-Gruppe.

Man erkennt, dass die Gruppe sogar kompakt ist, da der Einheitskreis eine kompakte Teilmenge der Ebene ist.

Da der Einheitskreis als Teilraum der reellen Zahlen sogar als riemannsche Untermannigfaltigkeit aufgefasst werden kann, erhält man eine Exponentialabbildung $\operatorname{exp}$ vom Tangentialraum im Punkt (1,0) in die Kreisgruppe. Identifiziert man bei dieser Wahl der riemannschen Metrik die Elemente des Tangentialraums auf kanonische Weise mit den reellen Zahlen, so ist $\operatorname {exp}\colon \mathbb{R} \to {\mathbb {S}}$ sogar ein surjektiver Homomorphismus, $\mathbb {S}$ wird also eine Einparameter-Gruppe.

Die Lie-Algebra besteht aus den Matrizen der Form

${\begin{pmatrix}0&a\\-a&0\end{pmatrix}}$ ,

wobei die Lie-Klammer durch den Kommutator gegeben ist, also stets gleich $0$ ist. Die Exponentialabbildung im Sinne der Theorie der Lie-Gruppen ist durch das Matrixexponential gegeben und entspricht genau der Exponentialabbildung im Sinne der riemannschen Geometrie.

Mittels der Exponentialabbildung ist die Gruppe der reellen Zahlen mit der Addition gerade die universelle Überlagerungsgruppe der Kreisgruppe. Hieraus lässt sich schließen, dass die Fundamentalgruppe des Kreises die Gruppe der ganzen Zahlen mit der Addition ist.

Als unitäre Gruppe

→ Hauptartikel: U(1)

Alternativ lässt sich die Kreisgruppe als die Gruppe $U(\mathbb{C} )$ oder U(1) der unitären Transformationen auf dem eindimensionalen Vektorraum der komplexen Zahlen definieren. Diese Transformationen lassen sich konkret als Matrizen mit einem Eintrag, d.h. durch komplexe Zahlen mit der üblichen Multiplikation darstellen:

${\mathbb {S}}=U(\mathbb{C} )=U(1)=\left\{c\in \mathbb{C} \mid |c|=1\right\}$

Mit der eulerschen Formel gilt

${\mathbb {S}}=\left\{e^{{\phi {\mathrm {i}}}}\mid \phi \in \mathbb{R} \right\}$ .

Die Abbildung $\phi {\mathrm {i}}\mapsto e^{{\phi {\mathrm {i}}}}$ , wobei die imaginäre Einheit $\mathrm {i}$ als Einheitstangentialvektor an der Stelle interpretiert wird, ist gerade die Exponentialabbildung. In der Gaußschen Zahlenebene kann die Multiplikation mit $e^{{\phi {\mathrm {i}}}}$ gerade als Drehung um den Winkel $\phi$ aufgefasst werden. Die Lie-Algebra besteht in dieser Beschreibung der Gruppe aus den imaginären Zahlen.

Charaktere

→ Hauptartikel: Charakter (Mathematik)

Begriff des Charakters

Die harmonische Analyse betrachtet unitäre Darstellungen von lokalkompakten topologischen Gruppen, d.h. stetige Homomorphismen von der Gruppe in die unitäre Gruppe über einem Hilbertraum versehen mit der starken Operatortopologie. Aufbauend darauf wird die verallgemeinerte Fourier-Transformation von Funktionen auf der Gruppe mittels der irreduziblen Darstellungen der Gruppe definiert. Eine besondere Rolle spielen die eindimensionalen Darstellungen, d.h. Darstellungen in die Kreisgruppe, genannt Charaktere. Diese sind stets irreduzibel. Aus dem Lemma von Schur folgt umgekehrt, dass jede irreduzible, stark-stetige unitäre Darstellung einer abelschen lokalkompakten topologischen Gruppe eindimensional, also ein Charakter ist. Für den abelschen Fall reduziert sich die Fourier-Transformation also auf ein Funktional auf den Charakteren.

Charaktere der Kreisgruppe

Einerseits wird die Kreisgruppe zur Definition des Charakters verwendet, andererseits hat die Kreisgruppe auch Charaktere. Die Charaktere der Kreisgruppe ${\mathbb T}$ sind genau die stetigen Homomorphismen ${{\mathbb T}}\rightarrow {{\mathbb T}}$ , und die kann man alle angeben. Jeder Charakter von ${\mathbb T}$ hat die Form $\chi_n(z) = z^n$ für ein $n\in {\mathbb Z}$ . Daher kann man die Menge der Charaktere mit $\mathbb {Z}$ identifizieren. Dass die Menge der Charaktere wieder eine Gruppenstruktur trägt, ist kein Zufall; es handelt sich um einen Spezialfall der allgemeineren Pontrjagin-Dualität.

Periodische Funktionen und Fourier-Reihe

Periodische Funktionen lassen sich als Funktionen auf der Kreislinie definieren. Beachtet man die topologische Struktur, erhält man einen natürlichen Stetigkeitsbegriff, beachtet man zudem die Gruppenstruktur, über das Haarmaß einen natürlichen Integrierbarkeitsbegriff (alternativ auch einfach über den Integralbegriff auf riemannschen Mannigfaltigkeiten oder das Lebesgue-Integral auf den reellen Zahlen eingeschränkt auf ein abgeschlossenes Intervall) und unter Beachtung der differenzierbaren Struktur auch einen natürlichen Differenzierbarkeitsbegriff.

Da die Kreisgruppe abelsch ist, ist die abstrakte Fourier-Transformation allein durch Charaktere auf der Kreisgruppe selbst gegeben. Man kann zeigen, dass jeder Charakter $\chi \colon {\mathbb {S}}\to {\mathbb {S}}$ auf der Kreisgruppe differenzierbar ist, somit folgt aus der Homomorphieeigenschaft

$\chi (x)=\operatorname {exp}(\operatorname {arg}(x)(D\chi )(1))$ ,

wobei $\operatorname{arg}$ die Argumentfunktion bezeichne. Aus der Periodizität der Funktion folgt, dass die Ableitung beim neutralen Element ein ganzzahliges Vielfaches von $\mathrm {i}$ sein muss, die Charaktere sind also gegeben durch

$\chi _{m}(x):=\operatorname {exp}(m\operatorname {arg}(x){\mathrm {i}})=x^{m},\ m\in \mathbb{Z }$ .

Diese bilden eine Orthonormalbasis des Raumes $L^{2}({\mathbb {S}})$ der quadratintegrablen komplexwertigen Funktionen auf der Kreisgruppe (vorausgesetzt das Maß von ganz $\mathbb {S}$ ist auf normiert), d.h. jede quadratintegrable periodische Funktion lässt sich durch ihre Fourier-Transformierte darstellen, die in diesem Fall Fourier-Entwicklung genannt wird, die Rücktransformation lässt sich, da es nur abzählbar viele Charaktere gibt, als Reihe, der sogenannten Fourier-Reihe darstellen. Elementar, d.h. ohne Verwendung von Sätzen aus der harmonischen Analyse wie dem Satz von Peter-Weyl oder der Pontrjagin-Dualität, folgt die Vollständigkeit aus dem Satz von Stone-Weierstraß.

Auftreten in der Physik

In der Quantenfeldtheorie auftretende Lagrangedichten enthalten oftmals eine globale Eichsymmetrie in Gestalt der Kreisgruppe, d.h. multipliziert man ein Feld an jeder Stelle mit einem Element der Kreisgruppe aufgefasst als komplexe Zahl, bleiben die Lagrangedichte und damit auch die Wirkung unverändert. Das Noethertheorem liefert eine zu dieser Symmetrie zugehörige Erhaltungsgröße, welche oft als (insbesondere elektrische) Ladung aufgefasst werden kann, sowie einen lokal erhaltenen, das heißt der Kontinuitätsgleichung genügenden Strom. Die Invarianz der Lagrangedichte heißt nichts anderes, als dass sie nur von den Betragsquadraten der jeweiligen komplexen Feldgrößen abhängt (in der Quantenfeldtheorie werden die Felder schließlich als operatorwertige Distributionen aufgefasst, in diesem Fall geht es um das Quadrat des Betrags der jeweiligen Operatoren, d.h. $A^{*}A$ für einen Operator ). Eine solche Eichsymmetrie tritt in der Quantenelektrodynamik auf.

Basierend auf einem Artikel in:

Wikipedia.de