
Fourierreihe

Als Fourierreihe, nach Joseph Fourier (1768–1830), bezeichnet man die Reihenentwicklung einer periodischen, abschnittsweise stetigen Funktion in eine Funktionenreihe aus Sinus- und Kosinusfunktionen. Die Basisfunktionen der Fourierreihe bilden ein bekanntes Beispiel für eine Orthonormalbasis. Im Rahmen der Theorie der Hilberträume werden auch Entwicklungen nach einem beliebigen vollständigen Orthonormalsystem als Fourierreihe bezeichnet. Eine Verallgemeinerung ist die Fourier-Transformation. Die Lehre der Fourierreihen ist Teil der Fourier-Analyse (klassische harmonische Analysis).
Geschichte
Bereits im 18. Jahrhundert kannten Mathematiker wie Euler, Lagrange oder die Bernoullis Fourierreihen für einige Funktionen. Zu Beginn des 19. Jahrhunderts behauptete nun Fourier in seinem Werk Théorie analytique de la chaleur (1822), dass es für alle Funktionen solche Reihenentwicklungen gäbe. Diese Behauptung stieß zunächst bei führenden Mathematikern wie Cauchy und Abel auf Ablehnung.
Dirichlet konnte 1829 beweisen, dass Fouriers Behauptung zumindest für Lipschitz-stetige Funktionen zutrifft. Du Bois-Reymond fand 1876 eine stetige Funktion, deren Fourierreihe divergiert. Im 20. Jahrhundert gelangte man schließlich zur Erkenntnis, dass es auch für stetige oder stückweise stetige Funktionen konvergente Fourierreihen gibt, wenn der Konvergenzbegriff geeignet abgeschwächt wird (Lennart Carleson).
Als eine frühe geometrische Vorform der Approximation durch eine Fourierreihe kann die Epizykeltheorie betrachtet werden.
1870 zeigte Georg Cantor die Eindeutigkeit der Darstellung einer Funktion durch ihre Fourierreihe, falls die Fourierreihe punktweise gegen die Funktion konvergiert. Wenig später zeigte er, dass dies auch bei endlich vielen Ausnahmestellen gilt, also Stellen, an an denen sich die Fourierreihen unterscheiden können oder die Fourierreihe nicht konvergiert. Die Frage, ob das auch für abzählbar unendlich viele Ausnahmestellen gilt, führte Cantor auf seine Begründung der Mengenlehre. Dabei zeigte er auch dass der Eindeutigkeitssatz auch bei abzählbar unendlich vielen Ausnahmestellen gilt, genauer für die von ihm eingeführten Punktmengen n-ter Art (allgemeiner bewiesen von Felix Bernstein und William Henry Young 1908 für abzählbar unendlich viele Ausnahmestellen). 1927 zeigte Nina Bari, dass auch bei bestimmten überabzählbar unendlichen Ausnahmemengen der Eindeutigkeitssatz erhalten bleibt.
Mathematische Hintergründe
+0,13sin(3x).png)
+0,4cos(2x).png)
2π-periodische Funktionen
Hilbertraum
Ausgangspunkt unserer Betrachtungen bilde die Menge
aller
-periodischen
Funktionen von
nach
.
Auf dieser Menge können wir eine Addition und eine Skalarmultiplikation
punktweise definieren, d.h.,
sei durch
und
durch
(mit
)
definiert. Mit diesen Abbildungen wird
zu einem
-Vektorraum.
Auf dem Vektorraum
definieren wir nun eine (partielle) Funktion
:
Zu beachten ist, dass
nicht auf ganz
definiert ist, weil das Integral
nicht für beliebige
existiert. Auf dem Unterraum
von
,
welcher durch
definiert ist, ist jedoch IMG class="text"
style="width: 6.4ex; height: 3ex; vertical-align: -1ex;" alt="\left\langle .,.\right\rangle _{{V}}"
src="/svg/54f210a516732fd160a6ac5fb948de1c1868b465.svg">
überall definiert. Wir werden uns daher für die weiteren Betrachtungen auf den
Unterraum
beschränken und definieren daher die Funktion
Es sei angemerkt, dass
eine positiv
semidefinite hermitesche Sesquilinearform ist. Es gilt:
Wir definieren
und
Die Abbildung
ist daher eine positiv definite hermitesche Sesquilinearform.
wird mit
somit zu einem Prähilbertraum.
Da
vollständig ist, ist
sogar ein Hilbertraum.
Wir werden im Folgenden nicht streng zwischen den Funktionen in
und den Restklassen in
unterscheiden.
Orthonormalsystem
Betrachten wir nun die Menge .
(Diese Menge ist wohldefiniert, weil die Funktion
bzgl.
für alle
-periodisch
ist.) Da offensichtlich
gilt, erzeugt
einen Untervektorraum
von
.
Da die Vektoren in
linear unabhängig sind, ist
eine Basis von
.
hat daher Dimension
.
Für zwei beliebige Vektoren
gilt:
Bezüglich des inneren Produkts
ist
somit eine Orthonormalbasis von
.
Fourierreihe von 2π-periodischen Funktionen
Jede Funktion
können wir nun formal als Reihe darstellen:
Diese formale Reihe nennen wir Fourierreihe von .
Unter Ausnutzung der Sesquilinearität von
und der Orthonormalität von
folgt
und damit
Wir können daher die Werte von
ausrechnen. Es sei jedoch darauf hingewiesen, dass die Reihe
nicht notwendigerweise gegen
konvergiert. Daher ist es notwendig, das Konvergenzverhalten
für verschiedene Klassen von Funktionen zu untersuchen.
Es gilt jedoch, dass genau dann nur endlich viele
ungleich 0 sind, wenn
gilt. Dies folgt unmittelbar daraus, dass
von
erzeugt wird. Als Konsequenz konvergiert die Fourierreihe für
auf jeden Fall.
Fourier-Transformierte und Fourier-Koeffizienten von 2π-periodischen Funktionen
Die Funktion
welche die Koeffizienten der Fourierreihe einer -periodischen
Funktion
liefert, nennen wir die Fourier-Transformierte von
.
Die
nennen wir Fourier-Koeffizienten. Die Funktionen
bilden einen
-Vektorraum
bzgl. punktweiser Addition und Multiplikation.
Fourier-Transformation und inverse Fourier-Transformation von 2π-periodischen Funktionen
Die Abbildung
welche die Funktionen
in ihre Fourier-Transformierten
überführt, nennen wir die Fourier-Transformation (von
-periodischen
Funktionen). Die Fourier-Transformation ist eine lineare Abbildung zwischen zwei
-Vektorräumen,
d.h., es gilt
Da die Fourierreihen von Funktionen
bzgl. der
-Norm
fast überall gegen
konvergieren, folgt, dass
gilt. Andernfalls wäre die Fourierreihe nämlich nicht konvergent. Für die
Abbildung
bedeutet das, dass sie nicht surjektiv ist.
Weiters können wir eine lineare Abbildung
definieren. Die Abbildung
nennen wir inverse Fourier-Transformation (von
-periodischen
Funktionen). Es gilt
.
Darstellungsformen
Die oben beschriebene Darstellung der Fourierreihe als Summe von komplexen
Exponentialfunktionen ist zwar in gewissem Sinne die mathematisch kompakteste
Darstellung, hat jedoch den Nachteil, dass im Allgemeinen auch für reellwertige
Funktionen komplexwertige Fourier-Koeffizienten
auftreten. Man kann die Fourierreihe aber auch anders darstellen.
Darstellung in Sinus-Kosinus-Form
Fourierreihen lassen sich auch in der Form
darstellen. Für die Fourier-Koeffizienten gilt dann
Man kann die Fourier-Koeffizienten durch
auch direkt ausrechnen. Wenn
reellwertig ist, erhält man somit reellwertige Fourier-Koeffizienten.
Darstellung in Amplituden-Phasen-Form
Für reellwertige Funktionen
ist des Weiteren eine Darstellung der Fourierreihe in der Form
mit
möglich. Wegen
folgt
mit
Es folgt daher
Der Winkel
ergibt sich zu
(Hinweis: In der Literatur findet man den Winkel
oftmals in Form des Arkustangens angegeben. Da die Tangensfunktion nur
-periodisch
ist, muss man bei einer solchen Darstellung Fallunterscheidungen vornehmen.
Wenn man den Winkel jedoch über den Arkuskosinus oder Arkussinus berechnet, hat
man den Vorteil, dass man keine Fallunterscheidungen vornehmen muss, weil die
Sinus- und Kosinusfunktion
-periodisch
sind!)
Verallgemeinerungen
Funktionen mit Periode T
Aufgrund der -Periodizität
der komplexen Exponentialfunktion wurde oben die Fourierreihe für
-periodische
Funktionen definiert, um eine einfache Darstellung zu erhalten. Da man eine
-periodische
Funktion
durch
in eine
-periodische
Funktion
überführen kann, stellt das keine Einschränkung dar.
Zudem kann die Fourierreihe einer -periodischen
Funktion
analog zum
-periodischen
Fall als
dargestellt werden.
Hierbei wird auf dem Raum
das Skalarprodukt
verwendet. Beim -periodischen
Fall definiert man
Wie im
-periodischen
Fall gilt nun (mit „neuen“
und Skalarprodukt)
Zusammenhang mit der Fourier-Transformation für nicht-periodische Funktionen
Mit Fourierreihen lassen sich nur periodische Funktionen und ihr Spektrum
beschreiben. Um auch nichtperiodische Funktionen spektral beschreiben zu können,
führt man einen Grenzübergang
der Periode
durch. Dadurch wird die Frequenzauflösung beliebig fein, was in einem
Verschwinden des komplexen Amplitudenspektrums resultiert. Aus diesem Grund
führt man das komplexe Amplitudendichtespektrum
ein, ausgehend von der komplexen Fourierreihe zunächst für die diskreten
Argumente
:
Durch Bildung des Grenzwertes
(wobei gleichzeitig
)
folgt damit unmittelbar die Fourier-Transformation:
Allgemeine innere Produkte
Wir haben die Fourierreihe für das innere Produkt
definiert. Man kann jedoch auch andere innere Produkte betrachten, was zur Folge hat, dass andere Vektoren zueinander orthogonal sind. Da die Fourier-Koeffizienten bezüglich eines Orthonormalsystems ermittelt werden, erhält man dadurch andere Koeffizienten. Da viele Eigenschaften der Fourier-Transformation auf der Ausnutzung der Orthogonalität der trigonometrischen Funktionen beruhen, ändern sich auch die Eigenschaften der Fourier-Transformation, wenn man andere innere Produkte verwendet.
Sei
ein Hilbertraum mit einer
Orthonormalbasis
.
Dann kann man jedes Element
des Hilbertraums durch
darstellen. Diese Reihendarstellung wird auch (verallgemeinerte) Fourier-Reihe genannt.
Fourierreihen und Symmetrie
Verallgemeinerungen der Fourier-Reihe, die sich zwar auch als Darstellungen in Orthonormalbasen beschreiben lassen, aber zusätzlich ähnlich der Fourier-Reihe bestimmte Eigenschaften in Bezug zu Symmetrien aufweisen, untersucht die harmonische Analyse. Die Pontrjagin-Dualität verallgemeinert dabei die Fourier-Reihe auf Funktionen auf beliebigen abelschen lokalkompakten topologischen Gruppen, der Satz von Peter-Weyl auf kompakten topologischen Gruppen.
Beispiele
Dreieckpuls
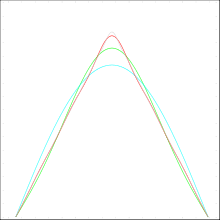
Die Dreieckfunktion
lässt sich je nach gewünschter Phasenlage mit Sinus- und Kosinustermen
approximieren. Mit dem Scheitelwert
lauten die Fourierreihen:
Rechteckpuls
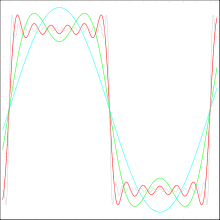
Die Rechteckschwingung ist definiert durch
Die Fourierreihe dazu lautet
Anhand dieser Funktion erkennt man, dass man eine Rechteckschwingung durch unendlich viele Harmonische darstellen kann. Sie enthält jeweils die ungeraden harmonischen Oberschwingungen, wobei die Amplitude mit steigender Frequenz abnimmt. Aufgrund dessen wird ein Rechtecksignal auch häufig zum Testen elektronischer Schaltungen genommen, da so das Frequenzverhalten dieser Schaltung erkannt wird.
Allgemein enthalten alle periodischen Schwingungen mit der Periodendauer
der Grundschwingung und beliebigem Verlauf innerhalb der Periode nur
ungeradzahlige Oberschwingungen, wenn gilt:
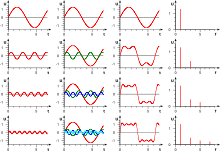
Im rechten Bild ist die Fourier-Synthese einer Rechteckschwingung dargestellt. Die Diagramme der ersten Spalte zeigen diejenige Schwingung, die in der jeweiligen Zeile hinzugefügt wird. Die Diagramme in der zweiten Spalte zeigen alle bisher berücksichtigten Schwingungen, die dann in den Diagrammen der dritten Spalte addiert werden, um dem zu erzeugenden Signal möglichst nahezukommen. Die Schwingung aus der ersten Zeile nennt sich Fundamentalschwingung, alle weiteren, die hinzugefügt werden, sind Oberschwingungen (Harmonische). Je mehr solcher Vielfache der Grundfrequenz berücksichtigt werden, umso näher kommt man einem idealen Rechtecksignal. An den unstetigen Stellen des Rechtecksignals bildet sich durch die Fourier-Synthese bedingt ein so genannter Überschwinger, der auch bei größerer Approximation nicht verschwindet. Diese Erscheinung wird Gibbssches Phänomen genannt, sie weist eine konstante und von der Bandbreite unabhängige Überschwingung von etwa 18 % des vollen Sprungs auf. Die vierte Spalte zeigt das Amplitudenspektrum normiert auf die Grundschwingung.
Sägezahnpuls (steigend)
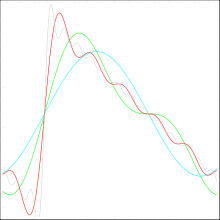
Ebenso lassen sich punktsymmetrische Funktionen aus Sinustermen approximieren. Hier erreicht man eine Phasenverschiebung durch alternierende Vorzeichen:
Sinuspuls
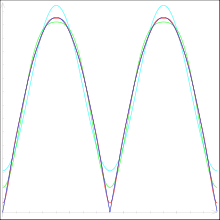
Konvergenzaussagen zur Fourierreihe
Man kann zwar bedenkenlos zu einer periodischen Funktion eine Fourierreihe
aufstellen, jedoch muss diese Reihe nicht konvergieren. Ist dies der Fall, so
erhält man durch diese Transformation auch keine weiteren Informationen.
Konvergiert die Reihe, so muss man sich im Klaren sein, in welchem Sinn die
Konvergenz vorliegt. Meistens untersucht man Fourierreihen auf punktweise
Konvergenz, gleichmäßige
Konvergenz oder auf Konvergenz bezüglich der -Norm.
Eine Fourierreihenentwicklung einer periodischen Funktion
mit Periode
ist in den folgenden, schrittweise allgemeiner werdenden Fällen möglich:
- Die stärkste Konvergenz ist die absolute
Konvergenz. Wenn
Hölder-stetig mit der Ordnung
ist, dann konvergiert die Fourierreihe von
absolut (und damit gleichmäßig) überall gegen
(Sergei Natanowitsch Bernstein).
- wenn
stetig und abschnittsweise stetig differenzierbar ist, dann konvergiert die Fourierreihe gleichmäßig (und damit punktweise) gegen
.
- wenn
eine beschränkte totale Variation über einer Periode hat, konvergiert die Fourierreihe der Funktion
punktweise für alle
gegen das Mittel aus links- und rechtsseitigem Grenzwert,
. Insbesondere konvergiert die Fourierreihe von
also überall dort gegen
, wo
stetig ist. Die Konvergenz ist zudem gleichmäßig auf jedem abgeschlossenen Intervall
, auf dem
stetig ist.
- wenn
, auf eine Periode
eingeschränkt, dem Funktionenraum
angehört, dann konvergiert die Fourierreihe im Sinne der L²-Norm gegen
.
Im Folgenden werden einige wichtige Sätze über die Konvergenz von Fourierreihen aufgezählt.
Satz von Dirichlet
Peter
Gustav Lejeune Dirichlet bewies, dass die Fourierreihe einer
differenzierbaren,
periodischen Funktion punktweise gegen die Ausgangsfunktion konvergiert.
Unter der Voraussetzung, dass
sogar stetig differenzierbar ist, kann die Aussage noch verbessert werden.
Sei
eine stetig differenzierbare,
-periodische
Funktion, dann konvergiert die Fourierreihe von
gleichmäßig gegen
.
Satz von Carleson
Der Satz von Carleson ist ein tiefliegendes Resultat zur Konvergenz einer Fourierreihe.
Sei
eine quadratintegrierbare
Funktion, dann konvergiert
die Fourierreihe von
fast überall.
Diese Aussage ist sogar für alle -Räume
mit
richtig und heißt in dieser allgemeinen Form Satz von Carleson–Hunt. Dass die
Aussage für
falsch ist, konnte Kolmogorov 1923 durch ein Gegenbeispiel zeigen. Nikolai
Nikolajewitsch Lusin vermutete schon 1915 die Richtigkeit des Satzes von
Carleson, konnte sie jedoch nicht beweisen. Der Beweis gelang erst Lennart Carleson im
Jahr 1966.
Satz von Fejér
Leopold
Fejér bewies, dass die arithmetischen
Mittel der Partialsummen der Fourierreihe einer stetigen, -periodischen
Funktion gleichmäßig gegen die Funktion konvergieren.
Sei
eine stetige,
-periodische
Funktion und
die Fourierreihe von
.
Mit
wird die n-te Partialsumme dieser Reihe beschrieben. Dann besagt der Satz von
Fejér, dass die Partialsummen
gleichmäßig gegen
konvergieren. Es gilt also
wobei die Konvergenz gleichmäßig ist.
Gibbssches Phänomen
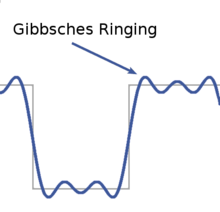
In der Umgebung von Sprungstellen entstehen dort in der Fourierreihe typische Über- und Unterschwinger von etwa 9 % der halben Sprunghöhe. Dieser Effekt hat weitreichende Auswirkungen in der Signalverarbeitung.
Mathematische Ursache dafür ist, dass für nicht stetige Funktionen
und
zwar Konvergenz im Sinne der -Norm
vorliegt, jedoch die Folge
im Allgemeinen nicht gleichmäßig konvergiert.
Literatur
- Thomas William Körner: Fourier analysis, Cambridge UP 1988
- Jörg Lange, Tatjana Lange: Fourier-Transformation zur Signal- und Systembeschreibung. Kompakt, visuell, intuitiv verständlich. Springer Vieweg 2019, ISBN 978-3-658-24849-9.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 07.12. 2022