Grenzwert einer Folge

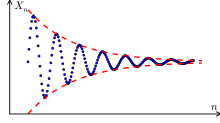
Beispiel einer Folge, die im Unendlichen gegen einen Grenzwert strebt.

Der Grenzwert oder Limes einer Folge von Zahlen ist eine Zahl, der die Folge beliebig nah kommt. Dies bedeutet, dass in jeder Umgebung des Grenzwerts fast alle Folgenglieder liegen. Besitzt eine Folge solch einen Grenzwert, so spricht man von Konvergenz der Folge – die Folge ist konvergent; sie konvergiert –, andernfalls von Divergenz. Ein Beispiel für eine konvergente Folge ist $a_{n}={\tfrac {1}{n}}$ , mit wachsendem n nähert sie sich der Zahl 0, dies ist also ihr Grenzwert. Eine solche Folge nennt man auch Nullfolge. Die konstante Folge $a_{n}=c$ konvergiert ebenfalls, ihr Grenzwert ist gerade die Zahl c. Hingegen divergiert die Folge $a_{n}=(-1)^{n}$ , da sie sich keiner Zahl annähert, sondern nur zwischen den Werten −1 und 1 alterniert („hin und her springt“). Der Grenzwert der Folge der Partialsummen einer Reihe heißt kurz Grenzwert der Reihe; entsprechend sind Konvergenz und Divergenz einer Reihe definiert.

Der Grenzwert einer Folge ist nicht nur für Zahlenfolgen definiert, sondern ganz genau so für Folgen, deren Glieder einem metrischen Raum angehören, d.h. dass zwischen ihnen ein reellwertiger Abstand definiert ist. In einer weiteren Verallgemeinerung genügt auch ein topologischer Raum; dort lässt sich auch ohne Metrik der Begriff Umgebung definieren, der hier gebraucht wird. Siehe dazu die Abschnitte Grenzwert einer Folge von Elementen eines metrischen Raumes und eines topologischen Raumes.

Die Konvergenz ist ein grundlegendes Konzept der modernen Analysis. Im allgemeineren Sinne wird es in der Topologie behandelt.

In der altgriechischen Philosophie und Mathematik stand der Grenzwertbegriff noch nicht zur Verfügung. In seiner modernen Form wurde er erstmals von Augustin-Louis Cauchy definiert.

Grenzwert einer reellen Zahlenfolge

Erläuterung und Definition

Illustration des Grenzwertes einer Folge

Jedes Glied $a_{n}$ einer Folge $(a_{n})_{n\in \mathbb {N} }$ reeller Zahlen hat einen Index . Die Zahl $a\in \mathbb{R}$ ist der Grenzwert dieser Folge, falls für jedes $\varepsilon >0$ alle Glieder mit hinreichend großem Index "um herum" in dem offenen Intervall $(a-\varepsilon ,a+\varepsilon )$ liegen. Also liegen dann auch nur endlich viele Folgenglieder außerhalb des Intervalls, und diese haben alle einen kleineren Index. Das Intervall $(a-\varepsilon ,a+\varepsilon )$ ist dabei die im Einleitungstext erwähnte Umgebung des Grenzwerts; genauer wird diese als $\varepsilon$ -Umgebung von a bezeichnet und dann $U_{\varepsilon }(a)$ geschrieben. Die Sprechenweisen " $(a_{n})_{n\in \mathbb {N} }$ hat den Grenzwert a" und " $(a_{n})_{n\in \mathbb {N} }$ konvergiert gegen a" sind genau gleichbedeutend.

Diese Konkretisierung lässt sich gut mit der anschaulichen Interpretation der Konvergenz als „Annäherung an den Grenzwert“ in Einklang bringen: Egal, wie man das $\varepsilon$ wählt, liegen ab einem gewissen Index alle Glieder stets in $(a-\varepsilon ,a+\varepsilon )$ , wobei ihr Abstand zu kleiner als $\varepsilon$ ist. So ergibt sich die exakte Definition:

Die Zahl $a\in \mathbb{R}$ heißt Grenzwert der Folge $(a_{n})_{n\in \mathbb {N} }$ , falls es zu jedem $\varepsilon >0$ eine natürliche Zahl so gibt, dass $\left|a_{n}-a\right|<\varepsilon$ , falls $n\geq N.$

Diese Definition fordert also: Zu jedem $\varepsilon >0$ gibt es einen Index mit der Eigenschaft, dass alle Folgenglieder mit dem Index oder einem größeren weniger als $\varepsilon$ von entfernt sind.

Dies ist so zu verstehen, dass als $\varepsilon$ eine beliebig kleine positive Zahl vorgegeben werden darf, und dass es dann stets möglich ist, ein genügend großes so anzugeben, dass $a_{N}$ und alle darauf folgenden Glieder die Bedingung erfüllen. Man sagt dann, dass fast alle Folgenglieder, also alle bis auf endlich viele Folgenglieder, die Bedingung erfüllen.

Hinweis 1: Wenn die Konvergenz einer Folge mit dieser Definition nachgewiesen werden soll, muss der Grenzwert im Vorhinein bekannt sein. Es gibt allerdings auch Kriterien, mit denen die Konvergenz einer Folge nachgewiesen werden kann, ohne dass der Grenzwert bekannt ist: siehe Konvergenzkriterien.

Hinweis 2: Die (durch die Häufigkeit ihrer Benutzung) auffällige Bezeichnung "kleiner" Zahlen durch den Buchstaben $\varepsilon$ hat sich allgemein eingebürgert und wird karikierend auch als Epsilontik bezeichnet.

Illustration

Beispiel einer Folge, die gegen den Grenzwert konvergiert.
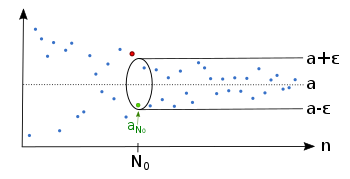Wenn wir ein $\varepsilon >0$ vorgeben, gibt es einen Mindestindex $N_{0}$ , so dass sich ab diesem Index die Folge im Epsilon-Schlauch $(a-\varepsilon ,a+\varepsilon )$ befindet.
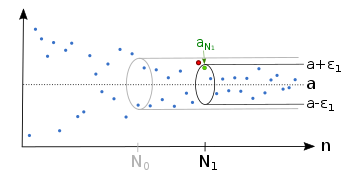Auch bei einem kleineren $\varepsilon _{1}>0$ gibt es einen Mindestindex $N_{1}$ , nach dem die Folge vollständig im Epsilon-Schlauch verläuft.
Egal welches $\varepsilon >0$ wir vorgeben, nur endlich viele Folgenglieder liegen außerhalb des Epsilon-Schlauchs $(a-\varepsilon ,a+\varepsilon )$ .

Eindeutigkeit des Grenzwertes

$(a-\epsilon ,a+\epsilon )\cap (b-\epsilon ,b+\epsilon )=\emptyset$

Der Grenzwert einer Folge $(a_{n})$ ist, sofern er existiert, eindeutig bestimmt.

Diese Aussage ergibt sich direkt aus der Definition anhand eines Widerspruchsbeweises. Hätte eine Folge $(a_{n})$ nämlich zwei verschiedene Grenzwerte $a \neq b$ , so besäßen diese einen Abstand $d=|a-b|>0$ . Betrachtet man nun $\epsilon$ -Umgebungen mit $\epsilon <{\tfrac {d}{2}}$ zu den beiden Grenzwerten, also im reellen Fall die Intervalle $(a-\epsilon ,a+\epsilon )$ und $(b-\epsilon ,b+\epsilon )$ , so besitzen diese keinen gemeinsamen Punkt. Nach der Definition des Grenzwerts müssen jedoch ab einem bestimmten Index alle Folgenglieder in der $\epsilon$ -Umgebung des Grenzwertes liegen und somit müssten die $\epsilon$ -Umgebungen von und unendlich viele gemeinsame Punkte haben. Dieser Widerspruch lässt sich nur beheben, wenn und keinen positiven Abstand besitzen, also a=b gilt.

Notation

Für den Grenzwert einer Folge $(a_{n})_{n\in \mathbb {N} }$ gibt es ein eigenes Symbol, man schreibt: $\lim _{{n\to \infty }}a_{n}=a$ .

Neben dieser Notation ist auch die Schreibweise $a_{n}\to a$ für $n\to \infty$ , gelesen als $a_{n}\;$ konvergiert gegen $a\;$ für gegen unendlich, oder kurz $a_{n}\to a$ üblich.

Mit dieser Schreibweise lässt sich die Definition des Grenzwertes einer Folge verkürzen: $\lim _{{n\to \infty }}a_{n}=a\quad \Longleftrightarrow \quad \forall \varepsilon >0\;\exists N\in {\mathbb {N}}\;\forall n\geq N:\;\left|a_{n}-a\right|<\varepsilon$ .

Unter Verwendung der Umgebungs-Schreibweise lautet die Definition: $\lim _{n\to \infty }a_{n}=a\quad \Longleftrightarrow \quad \forall \varepsilon >0\;\exists N\in \mathbb {N} \;\forall n\geq N:\;a_{n}\in U_{\varepsilon }(a)$ .

Beispiele

Die Definition des Grenzwertes soll an einem Beispiel deutlich gemacht werden, anschließend sind weitere Grenzwerte aufgeführt.

Um zu beweisen, dass die Folge ${\tfrac {1}{n}}$ gegen $0$ konvergiert, wählt man zu vorgegebenem $\varepsilon$ als irgendeine natürliche Zahl, die größer als ${\tfrac {1}{\varepsilon }}$ ist (die Existenz eines solchen ist durch das archimedische Axiom gesichert). Dann gilt für alle :

$|a_{n}-0|={\frac {1}{n}}<{\frac {1}{N}}<\varepsilon$

Die erste Ungleichung folgt dabei aus n>N , die zweite aus $N>{\tfrac {1}{\varepsilon }}$ . Hiermit ist die geforderte Existenz des Index gezeigt, die Zahl $0$ ist Grenzwert der Folge $a_{n}={\tfrac {1}{n}}$ .

Folgen, die gegen null konvergieren, wie ebendieses Beispiel ${\tfrac {1}{n}}$ , werden Nullfolgen genannt.

Die konstante Folge mit einer festen reellen Zahl konvergiert gegen .
Die Folge $(1;1{,}4;1{,}41;1{,}414;1{,}4142;1{,}41421;\dotsc )$ der abbrechenden Dezimalbruchentwicklungen von ${\sqrt {2}}$ konvergiert gegen ${\sqrt {2}}$ .
Die Folge $(e_{n})$ mit $e_{n}=\left(1+{\tfrac {1}{n}}\right)^{n}$ ist konvergent gegen die Eulersche Zahl . Die Folge $\left(1+{\tfrac {r}{n}}\right)^{n}$ konvergiert gegen $e^{r}$ . Diese Zahlenfolge tritt beim Problem der stetigen Verzinsung auf.
Die Folge $(c_{n})$ mit $c_{n}=(-1)^{n}+{\tfrac {1}{n}}$ ist nicht konvergent, besitzt jedoch zwei konvergente Teilfolgen für gerade und ungerade .

Rechenregeln

Für Grenzwerte gelten folgende Rechenregeln:

Existiert der Grenzwert $\lim _{{n\to \infty }}a_{n}=a$ , so existieren für jedes $c\in \mathbb{R} \;$ auch die folgenden Grenzwerte und können wie angegeben berechnet werden:

$\lim _{{n\to \infty }}ca_{n}=ca,$
$\lim _{{n\to \infty }}\left(c+a_{n}\right)=c+a,$
$\lim _{{n\to \infty }}\left(c-a_{n}\right)=c-a.$

Ist zusätzlich $a\neq 0$ , so ist auch $a_n\neq 0$ ab einem gewissen Index $N_{0}\;$ und für die Teilfolge der $n>N_{0}\;$ gilt

$\lim _{{n\to \infty }}{\frac {c}{a_{n}}}={\frac {c}{a}}.$

Existieren die Grenzwerte $\lim _{{n\to \infty }}a_{n}=a$ und $\lim _{{n\to \infty }}b_{n}=b$ , so existieren auch die folgenden Grenzwerte und können wie angegeben berechnet werden:

$\lim _{{n\to \infty }}\left(a_{n}+b_{n}\right)=a+b,$
$\lim _{{n\to \infty }}\left(a_{n}-b_{n}\right)=a-b,$
$\lim _{{n\to \infty }}\left(a_{n}\cdot b_{n}\right)=a\cdot b.$

Ist zusätzlich $b\neq 0$ , so ist auch $b_{n}\neq 0$ ab einem gewissen Index $N_{0}\;$ und für die Teilfolge der $n>N_{0}\;$ , dann gilt

$\lim _{{n\to \infty }}{\frac {a_{n}}{b_{n}}}={\frac {a}{b}}$ .

Mit Hilfe dieser Rechenregeln lassen sich in vielen Fällen aus bekannten Grenzwerten einfach weitere Grenzwerte berechnen. So erhält man beispielsweise für den Grenzwert der Folge ${\tfrac {2n^{2}-1}{n^{2}+1}}$

$\lim _{{n\to \infty }}{\frac {2n^{2}-1}{n^{2}+1}}=\lim _{{n\to \infty }}{\frac {2-{\frac {1}{n^{2}}}}{1+{\frac {1}{n^{2}}}}}={\frac {\lim _{{n\to \infty }}\left(2-{\frac {1}{n^{2}}}\right)}{\lim _{{n\to \infty }}\left(1+{\frac {1}{n^{2}}}\right)}}={\frac {2-\lim _{{n\to \infty }}{\frac {1}{n^{2}}}}{1+\lim _{{n\to \infty }}{\frac {1}{n^{2}}}}}={\frac {2-0}{1+0}}=2.$

Grenzwert einer beschränkten konvergenten Folge

Für die hier betrachteten Folgen ist Monotonie nicht vorausgesetzt.

Hat eine konvergente Folge $(a_{n})$ reeller Zahlen eine obere Schranke $\sigma$ (d.h. für alle $a_{n}$ gilt: $a_{n}\leq \sigma$ ), so ist $\lim _{n\to \infty }a_{n}=a\leq \sigma$ .

(Indirekter) Beweis: Annahme: $a>\sigma$ . Dann lässt sich ein $0<\epsilon =a-\sigma$ vorgeben, und für fast alle $a_{n}$ gilt (siehe oben Abschnitt "Erläuterung und Definition"):

$a_{n}>a-\epsilon =a-(a-\sigma )=\sigma$ (Widerspruch).

Hat eine konvergente Folge $(a_{n})$ reeller Zahlen eine untere Schranke $\sigma$ (d.h. für alle > $a_{n}$ gilt: $a_{n}\geq \sigma$ ), so ist $\lim _{n\to \infty }a_{n}=a\geq \sigma$ .

(Indirekter) Beweis: Annahme: $a<\sigma$ . Dann lässt sich ein $0<\epsilon =\sigma -a$ vorgeben, und für fast alle $a_{n}$ gilt (siehe oben Abschnitt "Erläuterung und Definition"):

$a_{n}<a+\epsilon =a+(\sigma -a)=\sigma$ (Widerspruch).

Wichtige Grenzwerte

$\lim _{{n\to \infty }}{\frac {1}{n}}=0$
$\lim _{{n\to \infty }}{\sqrt[ {n}]{n}}=1$
$\lim _{{n\to \infty }}\left(1+{\frac {z}{n}}\right)^{n}=e^{z}$ für komplexe (und damit insbesondere für reelle) Zahlen .
$\lim _{{n\to \infty }}n(a^{{{\frac 1{n}}}}-1)=\ln a$ für reelle
$\lim _{{n\to \infty }}\left(1+{\frac 12}+{\frac 13}+\dotsb +{\frac 1{n}}-\ln n\right)=\gamma$ (Euler-Mascheroni-Konstante)

Grenzwertbildung und Funktionsauswertung

Die Rechenregeln lassen sich als Spezialfall folgender Gesetzmäßigkeiten auffassen:

Ist $f\colon \mathbb{R} \to \mathbb{R} \;$ stetig im Punkt $a\;$ und konvergiert $a_{n}\;$ gegen $a\;$ , so gilt

$\lim _{{n\to \infty }}f(a_{n})=f\left(\lim _{{n\to \infty }}a_{n}\right)=f(a)$ ;

Ist $g\colon \mathbb{R} ^{2}\to \mathbb{R} \;$ stetig im Punkt $(a,b)\;$ und konvergieren $a_{n}\;$ gegen $a\;$ und $b_{n}\;$ gegen $b\;$ , so gilt

$\lim _{{n\to \infty }}g(a_{n},b_{n})=g\left(\lim _{{n\to \infty }}a_{n},\lim _{{n\to \infty }}b_{n}\right)=g(a,b)$ .

Für stetige Funktionen sind also Grenzwertbildung und Funktionsauswertung vertauschbar. Die oben angegebenen Rechenregeln folgen damit direkt aus der Stetigkeit der Addition, Subtraktion, Multiplikation und, falls der Nenner ungleich Null ist, Division.

In den reellen Zahlen gilt auch die Umkehrung: Ist die Funktion $f\colon \mathbb{R} \to \mathbb{R} \;$ gegeben und gilt für alle Folgen $(a_{n})_{n\in \mathbb {N} }$ mit $a_{n}\to a$ auch $\lim _{{n\to \infty }}f(a_{n})=f(a)$ , so ist $f\;$ stetig im Punkt $a\;$ .

Das Entsprechende gilt für jede Funktion $g\colon \mathbb{R} ^{2}\to \mathbb{R} \;$ : Gilt für alle Folgen $(a_{n})_{n\in \mathbb {N} }$ , $(b_{n})_{n\in \mathbb {N} }$ mit $a_{n}\to a$ und $b_{n}\to b$ auch $\lim _{{n\to \infty }}g\left(a_{n},b_{n}\right)=g(a,b)$ , so ist $g\;$ stetig im Punkt $(a,b)\;$ .

Konvergenzkriterien

Bei der oben angegebenen Definition der Konvergenz wird der Grenzwert $a\;$ in der Definition verwendet. Der Grenzwert muss also bekannt sein oder zumindest vermutet werden, damit mit dieser Definition die Konvergenz der Folge nachgewiesen werden kann. Es gibt allerdings auch Konvergenzkriterien, mit denen die Konvergenz einer Folge nachgewiesen werden kann, ohne dass der Grenzwert bekannt ist.

Das Monotoniekriterium besagt, dass eine monoton wachsende Folge genau dann konvergiert, wenn sie nach oben beschränkt ist. Der Grenzwert der Folge ist dann kleiner gleich der oberen Schranke. Formal gilt also:

$a_{n}\leq a_{{n+1}}{\text{ und }}a_{n}\leq A{\text{ für alle }}n\quad \Rightarrow \quad a_{n}{\text{ konvergiert und }}\lim _{{n\to \infty }}a_{n}\leq A$ .

Ebenso konvergiert eine monoton fallende und nach unten beschränkte Folge.

Das Cauchy-Kriterium beruht auf dem Begriff der Cauchy-Folge: Eine Folge $(a_{n})_{{n\in {\mathbb {N}}}}$ heißt Cauchy-Folge, wenn gilt:

$\forall \varepsilon >0\ \exists N\in {\mathbb {N}}:\ \forall n,m\in {\mathbb {N}},n>N,m>N:|a_{m}-a_{n}|<\varepsilon$ .

Das Cauchy-Kriterium besagt nun, dass eine Folge in den reellen Zahlen genau dann konvergiert, wenn sie eine Cauchy-Folge ist. Dieses Kriterium spielt insbesondere bei der Konstruktion der reellen Zahlen aus den rationalen Zahlen und bei der Erweiterung des Grenzwertbegriffs auf metrische Räume eine wichtige Rolle.

Bestimmung von Grenzwerten

Ist die Konvergenz einer Folge nachgewiesen lässt sich der Grenzwert in vielen Fällen näherungsweise bestimmen, indem in die Folge ein großes n eingesetzt wird und der Rest abgeschätzt wird. Beispielsweise ergibt sich für den Grenzwert $\lim _{{n\to \infty }}\left(1+{\frac 1{n}}\right)^{n}=e$ wegen der Abschätzung $\left(1+{\frac 1{n}}\right)^{n}<e<\left(1+{\frac 1{n}}\right)^{{n+1}}$ für n=1000 die Abschätzung $2{,}7169\dotso <e<2{,}7196\dotso$

Es gibt jedoch kein allgemeines Verfahren zur exakten Bestimmung von Grenzwerten. In vielen Fällen lässt sich die Regel von de l’Hospital anwenden. Manchmal ist es nützlich den Grenzwert in ein bestimmtes Integral umzuwandeln. Oft führen jedoch nur raffinierte Zerlegungen und Umformungen weiter.

Bestimmte Divergenz

In den reellen Zahlen unterscheidet man zwischen bestimmter Divergenz und unbestimmter Divergenz:

Bestimmte Divergenz gegen $+\infty$ (bzw. $-\infty$ ) liegt vor, wenn eine Folge x_n jede reelle Zahl irgendwann überschreitet und dann darüber bleibt (bzw. jede reelle Zahl unterschreitet und dann darunter bleibt). Das heißt,

$\forall M\in {\mathbb {R}}\ \exists N\in {\mathbb {N}}\quad \forall n>N:x_{n}>M$

bzw.

$\forall M\in {\mathbb {R}}\ \exists N\in {\mathbb {N}}\quad \forall n>N:x_{n}<M$ .

Man schreibt dann

$\lim _{{n\to \infty }}x_{n}=\infty$

bzw.

$\lim _{{n\to \infty }}x_{n}=-\infty$

und sagt, die Folge divergiert bestimmt gegen $\infty$ bzw. gegen $-\infty$ . Die Werte $\infty$ und $-\infty$ werden in diesem Zusammenhang oft auch uneigentliche Grenzwerte genannt beziehungsweise die bestimmte Divergenz als uneigentliche Konvergenz bezeichnet. Dass diese Werte ebenfalls als Grenzwert in einem etwas weiteren Sinne angesehen werden, ist insofern gerechtfertigt, als die uneigentlichen Grenzwerte in den erweiterten reellen Zahlen ${\bar {\mathbb{R} }}:=\mathbb{R} \cup \{-\infty ,+\infty \}$ , versehen mit einer passenden Topologie, echte Grenzwerte im Sinne des weiter unten beschriebenen allgemeinen topologischen Grenzwertbegriffs sind.

Unbestimmte Divergenz liegt vor, wenn die Folge weder konvergiert noch bestimmt divergiert.

Beispiele

Die Folge (n) der natürlichen Zahlen divergiert bestimmt gegen $\infty$ .
Die Folge (+1, −1, +1, −1, …) divergiert unbestimmt.
Die Folge (1, −2, 3, −4, 5, −6, …) divergiert unbestimmt.

Grenzwert und Häufungspunkt

Ein mit dem Grenzwert einer Folge eng verwandter Begriff ist der Häufungspunkt oder auch Häufungswert einer Folge. Die formalen Definitionen unterscheiden sich lediglich in der Position der Existenz- bzw. Allquantoren:

Während der Grenzwert als

$\left(\lim _{{n\to \infty }}a_{n}=a\right)\quad :\Longleftrightarrow \quad \forall \varepsilon >0\;\exists N\in {\mathbb {N}}\;\forall n>N:\;\left|a_{n}-a\right|<\varepsilon$

definiert ist, gilt für den Häufungspunkt „nur“

$a\;$ ist Häufungspunkt von $a_{n}:\Longleftrightarrow \quad \forall \varepsilon >0\;\forall N\in {\mathbb {N}}\;\exists n>N:\;\left|a_{n}-a\right|<\varepsilon$ .

Die Definition des Grenzwertes verlangt also, dass in jeder Umgebung des Grenzwertes ab einem gewissen Index alle Folgenglieder liegen; die Definition des Häufungspunktes verlangt lediglich, dass in jeder Umgebung unendlich viele Folgenglieder liegen.

Analog zu den uneigentlichen Grenzwerten werden gelegentlich die uneigentlichen Häufungspunkte definiert:

$+\infty \;$ ist uneigentlicher Häufungspunkt von $a_{n}\Longleftrightarrow \forall M\in {\mathbb {R}}\ \forall N\in {\mathbb {N}}\quad \exists n>N:\quad x_{n}>M$ ,

$-\infty \;$ ist uneigentlicher Häufungspunkt von $a_{n}\Longleftrightarrow \forall M\in {\mathbb {R}}\ \forall N\in {\mathbb {N}}\quad \exists n>N:\quad x_{n}<M$ .

Auch die Definition des uneigentlichen Häufungspunktes unterscheidet sich von der Definition des uneigentlichen Grenzwertes nur durch die Position der Existenz- bzw. Allquantoren.

Wenn eine Folge einen eigentlichen (bzw. uneigentlichen) Grenzwert hat, so ist dieser Grenzwert auch eigentlicher (bzw. uneigentlicher) Häufungspunkt. Während eine Folge aber höchstens einen Grenzwert hat, kann sie mehrere Häufungspunkte haben. Für jeden eigentlichen (bzw. uneigentlichen) Häufungspunkt gibt es eine Teilfolge, die gegen diesen Häufungspunkt konvergiert (bzw. bestimmt divergiert). Enthält umgekehrt eine Folge eine konvergente (bzw. bestimmt divergente) Teilfolge, so ist der (eigentliche bzw. uneigentliche) Grenzwert dieser Folge ein (eigentlicher bzw. uneigentlicher) Häufungspunkt der Folge.

Nach dem Satz von Bolzano-Weierstraß enthält jede beschränkte reelle Folge eine konvergente Teilfolge. Ist die Folge nach oben unbeschränkt, enthält sie eine gegen $+\infty$ bestimmt divergente Teilfolge, ist sie nach unten unbeschränkt, so enthält sie eine gegen $-\infty$ bestimmt divergente Teilfolge. Jede reelle Folge hat somit mindestens einen eigentlichen oder uneigentlichen Häufungspunkt. Der größte dieser Häufungspunkte wird als Limes superior bezeichnet, der kleinste als Limes inferior. Eine formale Definition dazu findet sich im Artikel Limes superior und Limes inferior. Stimmen der Limes superior und der Limes inferior überein, so ist dieser Wert auch eigentlicher oder uneigentlicher Grenzwert und die Folge ist konvergent bzw. bestimmt divergent. Sind Limes superior und der Limes inferior unterschiedlich, so ist die Folge unbestimmt divergent.

Grenzwert einer rationalen Zahlenfolge

Der Grenzwert einer Folge rationaler Zahlen wird formal wie der Grenzwert einer Folge reeller Zahlen definiert:

$\left(\lim _{{n\to \infty }}a_{n}=a\right)\quad \Longleftrightarrow \quad \forall \varepsilon >0\;\exists N\in {\mathbb {N}}\;\forall n>N:\;\left|a_{n}-a\right|<\varepsilon$

Während das bei $a_{n}\;$ und $\varepsilon \;$ keine besondere Einschränkung ist, wirkt sich das beim Grenzwert $a\;$ wesentlich aus. So gibt es keine rationale Zahl, gegen welche die oben angegebene Folge (1, 1.4, 1.41, 1.414, 1.4142, 1.41421, …) der abbrechenden Dezimalbruchentwicklungen von √2 konvergiert. Die Folge ist also in den rationalen Zahlen divergent, obwohl sie sowohl monoton wachsend und beschränkt ist, also das Monotoniekriterium erfüllt, als auch eine Cauchy-Folge ist, also auch das Cauchy-Kriterium erfüllt. Die rationalen Zahlen weisen somit „Lücken“ auf.

Diese „Lücken“ waren bereits Euklid in der Antike bekannt; es gelang aber erst im 19. Jahrhundert diese „Lücken“ durch die systematische Einführung der reellen Zahlen zu schließen. Ein häufig verwendeter Weg der systematischen Einführung der reellen Zahlen besteht darin, zuerst Cauchy-Folgen rationaler Zahlen zu betrachten, jene Cauchy-Folgen als äquivalent zu betrachten, deren Differenzen eine Nullfolge bilden, und darauf aufbauend die reellen Zahlen als Klassen äquivalenter Folgen zu definieren. In dieser Zahlbereichserweiterung gelten dann das oben angegebene Monotonie- und Cauchy-Kriterium; insbesondere dass nun jede Cauchy-Folge konvergent ist.

Für die Aussage, ob eine Folge konvergiert, ist es also wichtig zu wissen, welcher Zahlenbereich betrachtet wird; eine Folge, die in den reellen Zahlen konvergent ist, kann in den rationalen Zahlen divergent sein. Wenn nichts anderes dazugesagt wird, werden aber üblicherweise Grenzwerte über den reellen Zahlen betrachtet, da diese für die meisten Anwendungen das geeignetere Modell sind.

Grenzwert einer komplexen Zahlenfolge

Der Grenzwert einer Folge komplexer Zahlen wird formal ebenfalls wie der Grenzwert einer Folge reeller Zahlen definiert:

$\left(\lim _{{n\to \infty }}a_{n}=a\right)\quad \Longleftrightarrow \quad \forall \varepsilon >0\;\exists N\in {\mathbb {N}}\;\forall n>N:\;\left|a_{n}-a\right|<\varepsilon$

$a_{n}\;$ und $a\;$ bezeichnen dabei komplexe Zahlen, $\varepsilon \;$ ist weiterhin eine reelle Zahl. Eine Schreibweise der Art $a-\varepsilon <a_{n}<a+\varepsilon \;$ ist hier nicht mehr möglich, da sich auf den komplexen Zahlen keine geeignete Ordnungsrelation definieren lässt. Aus dem gleichen Grund lassen sich die Begriffe monoton steigend und fallend auf den komplexen Zahlen nicht geeignet definieren, daher ist auch das Monotoniekriterium nicht mehr anwendbar. Sehr wohl gilt aber weiterhin das zweite Hauptkriterium: eine Folge komplexer Zahlen ist genau dann konvergent, wenn sie eine Cauchy-Folge ist. Ein weiteres Konvergenzkriterium für komplexe Zahlen ist, dass eine Folge komplexer Zahlen genau dann konvergent ist, wenn sowohl die Folge der Realteile als auch die Folge der Imaginärteile konvergiert.

Grenzwert einer Folge von Elementen eines metrischen Raumes

Der Abstand zwischen den Folgengliedern und dem Grenzwert wurde als Betrag der Differenz angegeben. Sind die Folgenglieder keine reellen Zahlen, sondern z.B. Punkte in einem dreidimensionalen Raum, so wird der Betrag der Differenz durch eine Norm der Differenz oder noch allgemeiner durch eine Metrik ersetzt. Eine Folge wird dann als konvergent gegen einen Grenzwert a definiert, wenn in jeder ε-Umgebung von a fast alle Folgenglieder liegen.

Definition der Konvergenz

Sei (X, d) ein metrischer Raum. Eine Folge $(a_{n})$ in heißt konvergent gegen den Grenzwert $a\in X$ , wenn gilt:

$\forall {\varepsilon >0}\ \exists \ N\in {\mathbb {N}}\;\forall \ n>N:\;d(a,a_{n})<\varepsilon \,,$

in Worten: Es gibt für jedes beliebige (noch so kleine) $\varepsilon$ einen Index (i.A. abhängig von $\varepsilon$ ), derart, dass für alle Indizes n>N , alle weiteren Folgenglieder, gilt: der Abstand $d(a,a_{n})$ ist kleiner als $\varepsilon$ .

Dies entspricht der oben angegebenen Definition der Konvergenz einer Folge reeller Zahlen, es wird lediglich $|a_{n}-a|<\varepsilon$ durch $d(a_{n},a)<\varepsilon$ ersetzt.

Auch hier ist neben der Schreibweise $\lim _{{n\to \infty }}a_{n}=a$ die Schreibweise $a_{n}\to a$ , ebenfalls gelesen als $a_{n}$ konvergiert gegen $a\;$ , üblich.

Cauchy-Folgen und Vollständigkeit

Analog zu den reellen Zahlen spielt der Begriff der Cauchy-Folge in metrischen Räumen eine wichtige Rolle. Eine Folge heißt Cauchy-Folge, wenn

$\forall \varepsilon >0\ \exists N\in {\mathbb {N}}\ \forall n,m\in {\mathbb {N}},n>N,m>N:\quad d(a_{m},a_{n})<\varepsilon$ .

Hat jede Cauchy-Folge einen Grenzwert, so wird der metrische Raum als vollständig bezeichnet. Insbesondere sind die reellen und die komplexen Zahlen vollständig, die rationalen Zahlen aber nicht. Ist der metrische Raum nicht vollständig, dann lässt er sich analog zur Konstruktion der reellen Zahlen aus den rationalen Zahlen in den vollständigen metrischen Raum einbetten, der durch die Äquivalenzklassen von Cauchy-Folgen bezüglich der Äquivalenzrelation

$(a_{n})\sim (b_{n}):\quad \Leftrightarrow \quad d(a_{n},b_{n})\to 0$

gebildet wird.

Absolute Konvergenz

Der Begriff der absoluten Konvergenz lässt sich zwar nicht unmittelbar auf metrische Räume übertragen, für vollständige metrische Räume gibt es aber ein eng verwandtes Resultat: Eine Folge $\left(a_{n}\right)_{{n\in \mathbb{N} }}$ ist zumindest dann konvergent, wenn die Summe

$\sum _{{n\in \mathbb{N} }}d\left(a_{n},a_{{n+1}}\right)$

konvergiert. Aus der Konvergenz dieser Summe folgt nämlich, dass für jedes $\varepsilon > 0\;$ ein $N\;$ existiert, sodass für $m>n>N\;$ die Beziehung

$\sum _{{\nu =n}}^{{m-1}}d\left(a_{v},a_{{v+1}}\right)<\varepsilon$

gilt. Durch mehrfache Anwendung der Dreiecksungleichung folgt

$d\left(a_{n},a_{m}\right)\leq \sum _{{\nu =n}}^{{m-1}}d\left(a_{v},a_{{v+1}}\right)<\varepsilon$ ,

$\left(a_{n}\right)_{{n\in \mathbb{N} }}$ ist somit eine Cauchyfolge und damit in einem vollständigen Raum konvergent.

Grenzwert einer Folge von Elementen eines topologischen Raumes

Definition

Der Grenzwertbegriff wird in der Topologie verallgemeinert. Ist ein topologischer Raum $(X,{\mathfrak T})$ , also eine Menge mit der Menge der in diesem topologischen Raum offenen Teilmengen ${\mathfrak {T}}$ gegeben, so wird der Grenzwert einer Folge von Elementen $a_{n}\in X$ gegen einen Grenzwert $a\in X$ folgendermaßen definiert:

$\lim _{{n\to \infty }}a_{n}=a\quad \Longleftrightarrow \quad \forall U\in {\mathfrak U}(a)\;\exists N\in \mathbb{N} \;\forall n>N\colon \;a_{n}\in U.$

$U\in {\mathfrak U}(a)$ sind dabei die sogenannten Umgebungen von , das sind die Mengen, für die eine Menge $O\in {\mathfrak T}$ mit $a\in O\subseteq U$ existiert.

Anstelle alle Umgebungen von zu betrachten, ist es für den Nachweis der Konvergenz oft zweckmäßiger, sich auf eine Umgebungsbasis ${\mathfrak B}(a)$ zu beschränken, also auf eine Teilmenge ${\mathfrak B}(a)\subseteq {\mathfrak U}(a)$ mit der Eigenschaft, dass für jede Umgebung $U\in {\mathfrak U}(a)$ eine Menge $B\in {\mathfrak B}(a)$ mit $B\subseteq U$ existiert. Es gilt dann die leichter nachweisbare äquivalente Formulierung

$\lim _{{n\to \infty }}a_{n}=a\quad \Longleftrightarrow \quad \forall B\in {\mathfrak B}(a)\;\exists N\in \mathbb{N} \;\forall n>N\colon \;a_{n}\in B.$

Dieser Grenzwertbegriff beinhaltet den Grenzwert einer Zahlenfolge und den Grenzwert einer Folge von Elementen eines metrischen Raumes als Spezialfälle. Insbesondere bildet in metrischen Räumen die Menge ${\mathfrak B}(a)=\{B_{\varepsilon }(a)\mid \varepsilon >0\}$ aller offenen Kugeln $B_{\varepsilon }(a):=\{x\in X\mid d(x,a)<\varepsilon \}$ eine Umgebungsbasis von . Verwendet man diese Umgebungsbasis, erhält man genau die oben angegebene Definition des Grenzwerts in metrischen Räumen.

Erfüllt eine Topologie das erste Abzählbarkeitsaxiom, so reichen Grenzwerte von Folgen aus, um damit die Topologie zu beschreiben, insbesondere gilt, dass ein Punkt genau dann in der abgeschlossenen Hülle ${\bar {A}}$ von liegt, wenn es eine Folge von Elementen $a_{n}\in A$ gibt, die gegen konvergiert. Insbesondere erfüllen metrische Räume das erste Abzählbarkeitsaxiom, da beispielsweise ${\mathfrak B}(a)=\{B_{{1/k}}(a)\mid k\in \mathbb{N} \}$ eine Umgebungsbasis von ist.

In allgemeinen topologischen Räumen gilt diese Charakterisierung abgeschlossener Mengen als Grenzwerte von Folgen nicht, dort müssen statt Grenzwerten von Folgen Grenzwerte verallgemeinerter Folgen, sogenannter Netze betrachtet werden.

In allgemeinen topologischen Räumen kann es auch sein, dass eine Folge mehrere Grenzwerte hat. So konvergiert beispielsweise in der trivialen Topologie von , in der lediglich die leere Menge sowie selbst offene Mengen sind, jede Folge gegen jedes $a\in X$ . Verlangt man aber zusätzlich, dass der topologische Raum das hausdorffsche Trennungsaxiom erfüllt, so hat in einem solchen topologischen Raum jede Folge höchstens einen Grenzwert. Insbesondere ist in metrischen Räumen das hausdorffsche Trennungsaxiom erfüllt.

Beispiele

Konvergenz von Funktionenfolgen

→ Hauptartikel: Funktionenfolge

Um das Verhalten von Funktionenfolgen zu beschreiben, gibt es mehrere Konvergenzbegriffe, da es zum einen mehrere Abstandsbegriffe in einem Funktionenraum gibt und ferner neben der Frage nach der Existenz des Grenzwerts auch Fragen nach den Eigenschaften der Grenzfunktion auftauchen. So ist die Grenzfunktion einer Folge von stetigen Funktionen nicht notwendigerweise stetig.

Konvergenz in der Stochastik

Um speziell bei Anwendungen in der Statistik angemessen darüber entscheiden zu können, ob Schätz- oder Testverfahren asymptotisch die richtigen Resultate liefern, insbesondere für Aussagen wie die Gesetze der großen Zahlen und die Zentralen Grenzwertsätze, haben sich verschiedene Konvergenzbegriffe in der Stochastik herausgebildet. Im Prinzip handelt es sich dabei ebenfalls um Grenzwerte von Funktionenfolgen, da Zufallsvariablen in der Stochastik als Funktionen eines Wahrscheinlichkeitsraums modelliert werden. Für die Anwendungen der Stochastik hat es sich aber als zweckmäßig herausgestellt, eigene Bezeichnungen und auch eigene Konvergenzbegriffe einzuführen. Beispiele hiefür sind die Konvergenz im p-ten Mittel, die Konvergenz in Verteilung, die Konvergenz in Wahrscheinlichkeit und die fast sichere Konvergenz.

Fréchet-Axiome

Ein sehr allgemeiner Grenzwertbegriff wird durch die Fréchet-Axiome definiert: Ein Raum wird als Raum mit Konvergenz im Sinne von Fréchet bezeichnet, wenn

Jede Folge mit Elementen aus höchstens einen Grenzwert hat,
Jede konstante Folge $x_{n}=x\in X$ gegen konvergiert, und
Jede Teilfolge einer konvergenten Folge ebenfalls konvergiert und den gleichen Grenzwert wie die Ausgangsfolge hat.

Dieser Grenzwertbegriff stimmt jedoch nicht mit dem Grenzwertbegriff der Topologie überein. Erstens können Folgen in Topologien, die das Hausdorff-Axiom nicht erfüllen, mehrere Grenzwerte haben. Zweitens reichen in Topologien, die das erste Abzählbarkeitsaxiom nicht erfüllen, Folgen alleine nicht aus, um die Topologie eindeutig zu beschreiben, sodass die Fréchet Axiome auf Netze erweitert werden müssen. Drittens gibt es Konvergenzbegriffe, die den Frechét-Axiomen genügen, aber nicht durch eine Topologie erzeugt werden können, beispielsweise die punktweise Konvergenz fast überall. sind die Zusatzkriterien beschrieben, die ein Raum mit Konvergenz im Sinne von Fréchet erfüllen muss, damit diese Konvergenz eindeutig durch eine Topologie erzeugt werden kann.

Allgemeines für die Praxis (Iterationsverfahren)

Oft weiß man nicht von vornherein, z.B. wenn bei einem Iterationsverfahren zu einem Eingangswert einer Größe in bestimmter Weise eine Korrektur $\delta I$ berechnet und der so gewonnene Wert als neuer Eingangswert genommen wird (also bei einer Folge $I_{n}\,\to \,I_{n}\,+\,\delta I_{n}=:I_{{n+1}}\to \dotsc \,,\,\,n=1,\dotsc$ ), ob dieses Verfahren konvergiert. D.h. man betrachtet eine offene Situation, in der weder bekannt ist, dass ein notwendiges Kriterium verletzt ist ( $\Rightarrow$ Nichtkonvergenz), noch, dass eines der hinreichenden Kriterien erfüllt ist ( $\Rightarrow$ Konvergenz). In einem solchen Fall empfiehlt es sich, pragmatisch vorzugehen (d.h. zum Beispiel mit dem Cauchy-Kriterium) und das Verfahren einfach „hinreichend nahe“ an dem vermuteten Konvergenzpunkt durchzuführen, wobei in der Praxis nicht bekannt sein muss, was „hinreichend nahe“ quantitativ bedeutet.

Siehe auch

Basierend auf einem Artikel in Wikipedia.de