Folge (Mathematik)

Als Folge oder Sequenz wird in der Mathematik eine Auflistung (Familie) von endlich oder unendlich vielen fortlaufend nummerierten Objekten (beispielsweise Zahlen) bezeichnet. Dasselbe Objekt kann in einer Folge auch mehrfach auftreten. Das Objekt mit der Nummer , man sagt hier auch: mit dem Index , wird -tes Glied oder -te Komponente der Folge genannt. Endliche wie unendliche Folgen finden sich in allen Bereichen der Mathematik. Mit unendlichen Folgen, deren Glieder Zahlen sind, beschäftigt sich vor allem die Analysis.

Ist die Anzahl der Glieder einer endlichen Folge, so spricht man von einer Folge der Länge , einer -gliedrigen Folge oder von einem -Tupel. Die Folge ohne Glieder, deren Index-Bereich also leer ist, wird leere Folge, 0-gliedrige Folge oder 0-Tupel genannt.

Beispiele

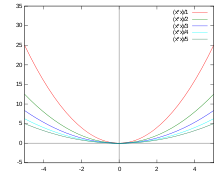
Kurven der ersten 5 Glieder der Funktionenfolge $f_{n}(x)={\tfrac {x^{2}}{n}}$

$(1,0,0,2,1)$ 5-Tupel von ganzen Zahlen

$(\sin ,\ \cos ,\ \tan ,\ \cot )$ 4-Tupel trigonometrischer Funktionen

$(2,3,5,7,11,13,\dotsc )$ Folge der Primzahlen

$(\{\},\{1\},\{1,2\},\{1,2,3\},\dotsc )$ Unendliche Folge von Mengen

$(x_{0},x_{1},x_{2},x_{3},\dotsc )$ Allgemeine unendliche Folge, deren Terme fortlaufend indiziert sind. Als Indizierungsbeginn ist hier die Null gewählt.

Schreibweise

Allgemein schreibt man für eine endliche Folge $\left(a_{i}\right)_{i=1,\dots ,n}$ , also $(a_1,a_2,\dotsc,a_n)$ , und bei unendlichen Folgen $\left(a_{i}\right)_{{i\in {\mathbb N}}}$ , also $(a_1,a_2,\dotsc)$ . Das $a_{i}$ steht dabei für ein beliebiges Folgenglied; die runde Klammer fasst diese zu einer Folge zusammen, dann wird der Laufbereich des Index dargestellt (dieser darf fehlen, wenn er implizit klar ist). Statt der runden Klammern werden manchmal auch spitze verwendet (also $\left\langle a_{i}\right\rangle _{i}$ ); statt der Kommas können Semikola verwendet werden, wenn eine Verwechslungsgefahr mit dem Dezimaltrennzeichen besteht.

Der Unterschied zu der Menge der Folgenglieder $\lbrace a_i \mid i \in \N\rbrace$ oder $\left\lbrace a_{i}\right\rbrace _{{i\in {\mathbb N}}}$ besteht darin, dass es auf die Reihenfolge der $a_{n}$ ankommt und dass mehrere Folgenglieder denselben Wert haben können.

Beispiel: Die Folge (0, 1, 0, 2, 0, 4, 0, 8, …) hat die Bildmenge (oder unterliegende Menge) {0, 1, 2, 4, 8, …}. Die Folge (1, 0, 2, 0, 0, 4, 0, 0, 0, 0, 8, …) hat dieselbe Bildmenge. In beiden Folgen tritt der Wert 0 mehrfach auf.

Formale Definition

Formal definiert ist eine unendliche Folge eine Abbildung,

${\begin{matrix}a\colon &\mathbb {N} &\to &X\\&i&\mapsto &a_{i},\end{matrix}}$

die jedem Index aus der als Indexmenge verwendeten Menge der natürlichen Zahlen $\mathbb {N}$ ein Folgenglied $a_{i}$ aus der Zielmenge zuordnet. Die Wahl des Anfangsindex ist jedoch letztlich willkürlich. In der Schulmathematik und in den häufigsten Anwendungsfällen ist die Menge der reellen Zahlen $\mathbb {R}$ . Es werden aber auch zum Beispiel Folgen von Mengen und Funktionenfolgen betrachtet.

Für eine endliche Folge (Tupel) mit Gliedern definiert man den Index statt aus $\mathbb {N}$ aus einer endlichen Menge, üblicherweise entweder aus der Menge $\{0, \dotsc, n-1\}$ oder aus der Menge $\{1, \dotsc, n\}$ . Gelegentlich findet sich für derartige Indexmengen die Notation $\langle n_\mathrm{min},n_\mathrm{max} \rangle$ .

Anwendungen

Unendliche Folgen können gegen einen Grenzwert konvergieren. Die Theorie der Grenzwerte unendlicher Folgen ist eine wichtige Grundlage der Analysis, denn auf ihr beruhen die Berechnung von Grenzwerten von Funktionen, die Definition der Ableitung (Differentialquotient als Grenzwert einer Folge von Differenzenquotienten) und der riemannsche Integralbegriff. Wichtige Folgen erhält man als Koeffizienten von Taylorreihen analytischer Funktionen. Manche elementare Funktionen führen dabei auf besondere Folgen, so die Tangens-Funktion auf die bernoullischen oder der Secans hyperbolicus auf die eulerschen Zahlen. Zum Beweis der Konvergenz einer Folge ist die Methode der vollständigen Induktion ein nützliches Hilfsmittel.

Eine Reihe ist eine spezielle Folge von Zahlen, deren -tes Glied sich aus der Summe der ersten Glieder einer anderen Zahlenfolge ergibt. Zum Beispiel ergibt sich die Reihe (1, 3, 6, 10, 15, …) aus der Folge (1, 2, 3, 4, 5, …). Reihen finden in vielen Bereichen der Mathematik Anwendung. Siehe dazu den Artikel Reihe (Mathematik).

Bildungsgesetz einer Folge

Es gibt mehrere Möglichkeiten eine Folge anzugeben:

Nennen aller Folgenglieder (nur für endliche Folgen möglich)
Funktionsgleichung
Reihe
Rekursion
Algorithmus

Eine endliche Folge kann man angeben, indem man sämtliche Folgenglieder nennt. Bei einer unendlichen Folge geht das nicht, stattdessen muss man das Bildungsgesetz der Folge in anderer Form mitteilen.

Folgen, deren Bildungsgesetz sich als Funktionsvorschrift oder Rekursion mitteilen lässt, werden zuweilen regelmäßige Folgen genannt.

Angabe von Anfangsgliedern

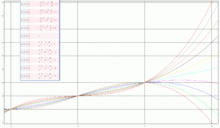
Als Lagrange-Polynome gewonnene Funktionvorschriften für zehn verschiedene Fortsetzungen der Folge 1,2,3; die Kurven zeigen den Verlauf der Polynome

Die in manchen Intelligenztests gestellte Aufgabe, eine Folge fortzusetzen, deren erste Glieder gegeben sind, ist aus mathematischer Sicht problematisch. Auch durch noch so viele Anfangsglieder ist der weitere Verlauf einer Folge nicht eindeutig festgelegt. Es gibt nur mehr oder weniger plausible Fortsetzungen.

Beispiele:

Gegeben ist 0, 1, 2, 3. Am plausibelsten ist die Fortsetzung 4, 5, 6, …, also die Folge aller natürlichen Zahlen. Möglich ist aber auch die Fortsetzung 0, 1, 2, 3, 0, …, und zwar als die periodische Folge der kleinsten positiven Reste der natürlichen Zahlen modulo 4. In einem Computer werden ganze Zahlen oft mit 32 Bit im Zweierkomplement, also als die absolut kleinsten Reste modulo 2³² dargestellt. Beim sukzessiven Erhöhen eines Registers durchläuft man dann die Zahlenfolge 0, 1, 2, 3, …, 2147483647, −2147483648, −2147483647, …, −1 und periodisch weiter.
Für die Zahlenfolge 3, 1, 4, 1, 5 ist eine plausible Fortsetzung 1, 6, 1, 7, … Andere würden die Dezimaldarstellung der Kreiszahl $\pi$ wiedererkennen und die Fortsetzung 9, 2, 6, … vorschlagen.

Die Online-Enzyklopädie der Zahlenfolgen (OEIS) enthält zigtausende mathematisch relevanter Folgen. Darin kann man nach einer gegebenen Teilfolge suchen.

Angabe einer Funktionsvorschrift

Für viele, aber keineswegs alle Folgen kann man die Funktionsvorschrift

$i\mapsto a_i$

als eine geschlossene Gleichung angeben.

In den folgenden Beispielen legen wir Indizes aus der Menge $\mathbb{N}_0$ zugrunde:

Die Folge der natürlichen Zahlen 0, 1, 2, 3, … Dieses Beispiel ist speziell, weil die Werte von Folgenglied und Index übereinstimmen. Die Funktionsvorschrift lautet einfach

Die Folge der ungeraden Zahlen 1, 3, 5, 7, … hat die Funktionsvorschrift

Die Folge der Zweierpotenzen 1, 2, 4, 8, …

Daran anknüpfende Aufgaben

Das Problem, zu einer gegebenen Funktionsvorschrift die Anfangsglieder zu bestimmen, ist einfach lösbar. Man nimmt nacheinander die Werte i=0 , i=1 , i=2 usw., setzt sie jeweils in die Funktionsvorschrift ein und berechnet auf diese Weise die Folgenglieder $a_{0}$ , $a_{1}$ , a_2 usw. Zweck dieser Rechnung ist es, sich ein erstes Bild vom Verlauf einer Folge zu machen. Aber Achtung: Eine Folge kann für wirklich große Indizes einen ganz anderen Verlauf nehmen als nach den ersten zehn oder hundert Gliedern zu erwarten war. Beispiel: die Folge a_i = 1 / (1 + (i - 1000)^2) , die bis i=1000 monoton zunimmt, dann aber wieder abnimmt, wie man durch Einsetzen höherer Zehnerpotenzen überprüfen kann.

Die Umkehraufgabe, zu gegebenen Anfangsgliedern eine Funktionsvorschrift zu bestimmen, ist dagegen deutlich schwieriger. Streng genommen kann es gar keine eindeutige Lösung geben, denn jeder Folgenanfang lässt sich wie oben beschrieben in verschiedener Weise fortsetzen. In der Praxis wird diese Aufgabe daher nur für Folgen gestellt, deren Glieder $a_{0}$ , $a_{1}$ , a_2 usw. in einigermaßen überschaubarer Weise vom Index $i=0, 1, 2, \dotsc$ abhängen. Im Einzelnen können folgende Eigenschaften überprüft werden:

Ist die Folge alternierend? Wenn ja, bekommt man das richtige Vorzeichen durch einen Faktor in der Funktionsvorschrift. Beispiel: 0, −1, 2, −3, 4, … hat die Vorschrift $a_i=(-1)^i \cdot i$ .
Sind die Folgenglieder Brüche? Wenn ja, konstruiere man unabhängig voneinander Funktionsvorschriften für Zähler und Nenner. Beispiel: 1/1, 2/2, 3/4, 4/8, … hat die Vorschrift .
Nehmen die Folgenglieder um konstante Differenzen zu (oder ab, mit )? Wenn ja, hat man eine arithmetische Folge $a_i=a_0 +d\cdot i$ . Beispiel: 1, 3, 5, 7, … hat die Vorschrift .
Genügen die Differenzen zwischen aufeinander folgenden Gliedern einem einfacheren Bildungsgesetz als die Folgenglieder selbst? Wenn ja, kann man die Folge als eine Reihe auffassen (siehe dazu unten). Beispiel: Für 1, 3, 6, 10, 15, … lauten die Differenzen 1, 2, 3, 4, …
Stehen aufeinander folgende Folgenglieder in einem konstanten Verhältnis zueinander? Wenn ja, hat man eine geometrische Folge $a_i=a_0 \cdot q^i$ . Beispiel: Die Folge 100; 80; 64; 51,2; … nimmt von Glied zu Glied um einen Faktor 0,8 ab; also lautet die Vorschrift $a_{i}=100\cdot {0{,}8}^{i}$ .

Erschwert wird die Suche nach einer Funktionsvorschrift dadurch, dass die ersten ein oder zwei Folgenglieder (zu den Indizes 0 und 1) oft aus dem Rahmen zu fallen scheinen. Das liegt daran, dass ein Summand 0, ein Faktor 1 oder Exponent 0 oder 1 in aller Regel nicht ausgeschrieben, sondern sofort ausgerechnet werden. In der gekürzten Form 1, 1, 3/4, 1/2, … ist dem oben genannten Beispiel 1/1, 2/2, 3/4, 4/8, … die Funktionsvorschrift schwer anzusehen.

Angabe als Reihe

Eine Folge $\left(s_{n}\right)_{{n\in {\mathbb N}}}$ , deren -tes Glied die Summe der ersten Glieder einer anderen Folge $\left(a_{i}\right)_{{i\in {\mathbb N}}}$ ist, heißt eine Reihe:

$s_n= a_0 + a_1 +\dotsb+a_n=\sum_{i=0}^n a_i$

Der mit Hilfe des Summenzeichens geschriebene Ausdruck $\sum\nolimits_{i=0}^n a_i$ ist also eine Abkürzung für den Ausdruck $a_0+a_1+\dotsb+a_n$ . Innerhalb und außerhalb des Summenzeichens sind unterschiedliche Indizes zu verwenden. Dass speziell und gewählt wurden, entspricht einer weit verbreiteten Konvention, ist aber nicht zwingend.

Um $s_n=\sum\nolimits_{i=0}^n a_i$ als konkreten Zahlenwert zu berechnen, muss ein konkreter Zahlenwert für den Index vorgegeben werden. Im Gegensatz dazu ist der Index kein (von außen) vorzugebender Wert, sondern durch die Summationsvorschrift selbst festgelegt. Welches auch immer gegeben ist, für den Laufindex müssen nacheinander die Werte 0, 1, …, eingesetzt und die Summe der zugehörigen $a_{0}$ , $a_{1}$ , …, $a_{n}$ berechnet werden.

Man kann jede Folge $\left(s_{n}\right)_{{n\in {\mathbb N}}}$ als eine Reihe auffassen, indem man aus den Differenzen aufeinander folgender Glieder eine zugehörige Folge

$a_{i}={\begin{cases}s_{0}&{\text{wenn }}i=0,\\s_{i}-s_{i-1}&{\text{sonst}}\end{cases}}$

konstruiert. Folge und Reihe sind also nicht scharf voneinander trennbar. Die Zeitreihen der Wirtschaftswissenschaftler sind eigentlich Folgen. Viele Erklärungsmodelle modellieren aber nicht absolute Werte, sondern deren zeitliche Veränderungen, was für die Auffassung der absoluten Werte als Glieder einer Reihe spricht.

Konkreten Nutzen bringt die Deutung einer Folge als Reihe, wenn man die Summation für beliebige ausführen kann. Summationsformeln sind zum Beispiel bekannt für die arithmetische Reihe und die geometrische Reihe.

Die Deutung einer unendlichen Folge als Reihe erleichtert es zu bestimmen, ob und wenn ja gegen welchen Grenzwert die Folge konvergiert. Für unendliche Reihen gibt es eigene Konvergenzkriterien. Umgekehrt kann man aus der Konvergenz einer Reihe (d.h., in obiger Schreibweise, der Konvergenz von $\left(s_{n}\right)_{{n\in {\mathbb N}}}$ ) immer darauf schließen, dass die Folge der Summanden (in obiger Schreibweise also die Folge $\left(a_{n}\right)_{{n\in {\mathbb N}}}$ ) gegen Null konvergiert.

Angabe einer Rekursion

Das Bildungsgesetz einer Folge kann auch rekursiv angegeben werden. Dazu nennt man Anfangswerte (mit $m \geq 1$ ; meistens ist m=1 oder m=2 ) sowie eine Vorschrift, wie ein Folgenglied a_i aus den vorhergehenden Gliedern $a_{i-m}, \dotsc, a_{i-1}$ berechnet werden kann.

Das bekannteste Beispiel für eine Folge, die sich wesentlich einfacher durch eine Rekursionsvorschrift als durch eine Funktionsvorschrift beschreiben lässt, ist die Fibonacci-Folge 0, 1, 1, 2, 3, 5, 8, … Für sie ist m=2 , gegeben sind die zwei Anfangsglieder a_0=0 und a_1=1 sowie die Rekursionsvorschrift

$a_i = a_{i-2} + a_{i-1}.$

Die explizite Formel von Moivre und Binet für die Folgenglieder

$a_i = \frac 1{\sqrt 5} \left(\left(\frac{1+\sqrt 5}2\right)^i - \left(\frac{1-\sqrt 5}2\right)^i\right) = \frac{\Phi^i - \bar\Phi^i}{\Phi - \bar\Phi}$

steht in engem Zusammenhang mit dem Goldenen Schnitt und der Goldenen Zahl $\Phi$ . Man beachte, dass die $a_{i}$ alle ganzzahlig sind, da sich die ungeraden Potenzen der $\sqrt 5$ heraussubtrahieren.

Für manche Folgen kann man umgekehrt aus der Funktionsvorschrift eine Rekursionsvorschrift ableiten. Zum Beispiel folgt für die geometrische Folge aus der Funktionsvorschrift

$a_i = a_0\cdot q^i$

die Rekursionsvorschrift

$a_i = q\cdot a_{i-1}.$

Die Rekursion

$a_1 = 2,\quad a_{i+1} = \frac{a_i}2 + \frac1{a_i}$

definiert die Folge rationaler Zahlen 2, 3/2, 17/12, …, die gegen ${\sqrt {2}}$ konvergiert.

Angabe über einen Algorithmus

Für manche Folgen gibt es eine klar definierte Konstruktionsvorschrift (Algorithmus), aber keine Funktionsvorschrift. Das bekannteste Beispiel ist die Folge der Primzahlen 2, 3, 5, 7, 11, … Bereits den alten Griechen (möglicherweise auch Indern) war es bekannt, wie man immer weitere Glieder dieser Folge berechnet. Eine Möglichkeit ist, das Sieb des Eratosthenes anzuwenden. Es gibt jedoch keine Methode, zu einem gegebenen die -te Primzahl anzugeben, ohne zuvor die gesamte Folge von der ersten bis zur (i-1) -ten Primzahl zu bestimmen. Wenn man nicht die zehnte oder die hundertste, sondern die $10^{20}$ -te Primzahl wissen möchte, erhöht dies den Rechenaufwand stark.

Die Länge des kürzesten Algorithmus, der eine Folge erzeugt, heißt ihre Kolmogorow-Komplexität (manchmal wird diese Bezeichnung in einem engen Sinn nur für Zeichenfolgen, d.h. endliche Folgen mit endlichen Zielmengen verwendet). Sie hängt zwar von der verwendeten Programmiersprache ab; nach dem Invarianztheorem differieren die Längen für unterschiedliche Sprachen jedoch nur um eine nur sprachabhängige additive Konstante.

Charakterisierung von Folgen

Wie Funktionen kann man auch Zahlenfolgen über ihr Steigungsverhalten und ihren Bildbereich charakterisieren.

Monotonie

→ Hauptartikel: Monotone Folge reeller Zahlen

Begriff

Eine Folge heißt monoton steigend, wenn sie von Glied zu Glied gleichbleibt oder zunimmt, wenn also für alle aus $\mathbb {N}$ gilt: $a_i \leq a_{i+1}$ . Die Folge heißt streng monoton steigend, wenn sie von Glied zu Glied zunimmt, wenn also für alle aus $\mathbb {N}$ gilt: $a_i < a_{i+1}$ . Die Begriffe monoton fallend und streng monoton fallend sind analog definiert. Der Begriff der Monotonie ist jedoch nicht auf reelle Zahlen beschränkt: Jede geordnete Menge erlaubt eine sinnvolle Verwendung des Begriffs.

Nachweis der Monotonie

Vermutet man, dass eine Folge nicht monoton (bzw. streng monoton) ist, setzt man ein paar Indizes in die Funktionsvorschrift ein, berechnet die zugehörigen Folgenglieder und hofft, ein Gegenbeispiel zu finden. Beispiel: Die durch a_i = 2^i /(3i +1) gegebene Folge ist nicht monoton, denn a_0 = 1 > a_2 = 4/7 aber a_2 < a_5 =32/16 .

Wenn man beispielsweise vermutet, dass eine Folge streng monoton fällt, schreibt man $a_i > a_{i+1}$ , wertet auf beiden Seiten die Funktionsvorschrift aus (indem man auf der rechten Seite i+1 anstelle von in die Vorschrift einsetzt), und überprüft die so entstandene Ungleichung, indem man sie durch Äquivalenzumformungen vereinfacht. Beispiel: $a_i=\tfrac{1}{i}$ führt auf $\textstyle \frac 1i > \frac{1}{i+1}$ , das ist äquivalent zu i+1 > i bzw. zur wahren Aussage 1 > 0 .

Manche Funktionsvorschriften lassen sich durch Termumformungen in eine Summe aus konstanten Termen und einer bekannten, einfacheren Folge zerlegen, deren Steigungsverhalten schon bekannt ist. Beispiel: $\textstyle a_i = \frac{2i+1}{i+1} = \frac {2(i+1)-1}{i+1} = 2 - \frac {1}{i+1}$ . Wenn man weiß, dass 1/(i+1) streng monoton fällt, kann man schließen, dass -1/(i+1) streng monoton steigt. Weil der Term 2 konstant ist, steigt auch $a_{i}$ > streng monoton.

Beschränktheit

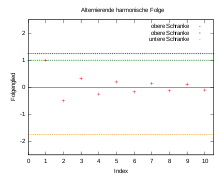
Die beschränkte Folge $a_n = (-1)^{n+1} \cdot \tfrac{1}{n}$ mit eingezeichneten Schranken.

Begriff

Eine Folge reeller Zahlen heißt nach oben beschränkt, wenn sie eine obere Schranke besitzt, so dass für alle aus $\mathbb {N}$ gilt: $a_i \leq S$ . Die kleinste obere Schranke einer Folge heißt auch ihr Supremum. Die Begriffe nach unten beschränkt, untere Schranke und Infimum sind analog definiert. Eine Folge, die zugleich nach oben und nach unten beschränkt ist, heißt beschränkt.

Nachweis der Beschränktheit und Bestimmung einer Schranke

Ein Nachweis per Gegenbeispiel ist hier nicht möglich, denn mit auch noch so vielen Beispielen kann man nicht sicherstellen, dass es nicht irgendeine sehr große bzw. sehr kleine Zahl gibt, durch die die Folge beschränkt ist.

Es muss also angenommen werden, dass es eine Schranke gibt. Nun wird die passende Ungleichung angesetzt, d.h. für eine obere Schranke also $a_i \leq S$ . Auf der linken Seite der Ungleichung wird die Funktionsvorschrift angewandt und dann nach aufgelöst. Dadurch erhält man (mit etwas Glück) ein Ergebnis der Form $i \leq f(S)$ oder $i \geq f(S)$ , wobei f(S) für einen von abhängigen Term steht. Im ersten Fall hat man herausgefunden, dass die Folge nicht nach oben beschränkt ist (egal wie groß f(S) ist, es ist immer möglich, ein noch größeres zu finden, das die Ungleichung verletzt). Im zweiten Fall versucht man ein zu finden, für das $f(S) \leq 0$ ist. Für dieses ist $i \geq f(S)$ immer erfüllt und somit ist der Nachweis gelungen, dass eine obere Schranke ist.

Auch hier lässt sich der Nachweis einfacher gestalten wenn es gelingt, die Funktionsvorschrift in eine Summe aus einfacheren Termen zu zerlegen.

Sonstige

Eine Folge, deren Werte abwechselnd positiv und negativ sind, heißt alternierend.
Eine Folge, deren Glieder alle übereinstimmen, wird konstante Folge genannt.
Eine Folge, deren Glieder alle ab einem bestimmten Glied übereinstimmen, wird stationäre Folge genannt
Eine Folge, die gegen 0 konvergiert, heißt Nullfolge.
Eine Folge, wird abbrechend genannt, falls sie ab einem bestimmten Glied 0 ist, d.h. eine stationäre Nullfolge.
Eine Folge, die aus Wiederholungen einer endlichen Teilfolge besteht, heißt periodisch. Es gibt eine Periodenlänge , und für alle aus $\mathbb {N}$ gilt: $a_i = a_{i+n}$ . Teilfolge ist hier als Folge von in die gewählte Menge zu verstehen.

Eine interessante Aufgabe aus der Analysis besteht darin, zu ermitteln, ob eine Folge konvergiert, und im Falle der Konvergenz, gegen welchen Grenzwert. Eine unendliche Folge, die nicht konvergiert, kann nichtsdestoweniger Häufungspunkte besitzen (Beispiel: die Folge −1/2, 3/4, −5/6, 7/8, … besitzt die Häufungspunkte −1 und 1). Insbesondere hat jede beschränkte Folge in der Menge der reellen Zahlen mindestens einen Häufungspunkt (Satz von Bolzano-Weierstraß).

Die vorgenannte Charakterisierung einer Folge über ihr Steigungsverhalten und ihren Bildbereich kann helfen, zu bestimmen, ob und falls gegen welchen Grenzwert sie konvergiert. Besonders nützlich ist hierbei das Monotoniekriterium, nach dem eine monoton steigende, nach oben beschränkte Folge in der Menge der reellen Zahlen stets konvergiert, wobei ihr Grenzwert mit ihrem Supremum übereinstimmt (Beispiel: die Folge 0, 1/2, 2/3, 3/4, … konvergiert gegen ihr Supremum 1). Entsprechend konvergiert eine monoton fallende, nach unten beschränkte Folge gegen ihr Infimum.

Die Charakterisierungskriterien Monotonie und Beschränktheit lassen sich verallgemeinern für alle Folgen, deren Zielmenge geordnet ist. Konstante, stationäre und periodische Folgen lassen sich für beliebige Zielbereiche, konvergente Folgen für einen beliebigen metrischen Raum als Zielbereich definieren.

Wichtige Folgen

Die meisten bekannten Zahlenfolgen können in der On-Line Encyclopedia of Integer Sequences (OEIS) von Neil Sloane nachgeschlagen werden. Diese Datenbank enthielt im Februar 2009 über 155.000 Beschreibungen von Zahlenfolgen.

Weitere oft genannte Zahlenfolgen sind etwa die konstanten Folgen mit der Funktionsvorschrift $a_{n}=a$ mit einer für alle festen Zahl und die durch $a_{n}=1/n$ ( $n\geq 1$ ) definierte harmonische Folge.

Arithmetische Folgen und Reihen

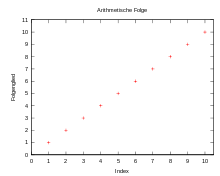
→ Hauptartikel: Arithmetische Folge

Die arithmetische Folge

Eine arithmetische Folge ist eine Folge mit konstanter Differenz zwischen aufeinanderfolgenden Gliedern. Beispiele sind die häufig verwendeten Folgen der geraden Zahlen 2, 4, 6, … mit der Funktionsvorschrift

und die der ungeraden Zahlen mit der Funktionsvorschrift

Allgemein lautet die Funktionsvorschrift

$a_i = a_0 + i \cdot d,$

wobei die konstante Differenz bezeichnet.

Folgen, die sich auf arithmetische Folgen zurückführen lassen, nennt man arithmetische Folgen höherer Ordnung. So ist die Folge der Dreieckszahlen eine arithmetische Folge 2. Ordnung.

Folge:	$1\$		$3\$		$6\$		$10\$		$15\$		$\dotso\$
1. Differenzfolge:		$2\$		$3\$		$4\$		$5\$		$\dotso \$
2. Differenzfolge:			$1\$		$1\$		$1\$		$\dotso\$

Arithmetische Folgen -ter Ordnung sind genau diejenigen Folgen, die sich durch ein Polynom -ten Grades beschreiben lassen. Dieses Polynom lässt sich durch Lagrange-Interpolation aus beliebigen Folgenglieder finden. Die Dreieckzahlen gehorchen z.B. dem Bildungsgesetz $a_i = \frac{i^2}{2} + \frac{i}{2}$ .

Folgen auf Basis der Potenzfunktion

Eine Potenzfolge ist eine Folge, für die die Potenzfunktion die Glieder liefert (Erzeugende Funktion)

Die Folge der Quadratzahlen: 0, 1, 4, 9, … hat die Funktionsvorschrift a_i = i^2 . Die Folge der Quadratzahlen ist ebenfalls eine arithmetische Folge 2. Ordnung, da sie sich als Reihe auffassen lässt, der die Folge der ungeraden Zahlen zugrunde liegt.

Die Folge der Kubikzahlen 0, 1, 8, 27, … besitzt die Vorschrift

was man für -te Potenzen der natürlichen Zahlen zu

verallgemeinern kann, wobei eine beliebige reelle Zahl sein darf. Mit s=1/2 erhält man die Folge $0, 1, \sqrt{2}, \sqrt{3}, 2, \sqrt{5}, \dotsc$ der Quadratwurzeln der natürlichen Zahlen,

$a_i = i^{0{,}5} = \sqrt i$ .

Bei negativen Exponenten s<0 ist zu beachten, dass 0^s nicht existiert. Beispielsweise ist es nicht möglich, mit s=-1 und der Funktionsvorschrift

$a_i = i^{-1} = \frac{1}{i}$ das Folgenglied zum Index i=0

zu berechnen. Man kann den Index 0 ausschließen, sich also auf die Indexmenge $\N^+$ beschränken. Oft ist es jedoch zweckmäßiger, die Indexmenge $\mathbb {N} _{0}$ unverändert zu lassen und stattdessen die Funktionsvorschrift in

$a_i = (i+1)^{-1} = \frac{1}{i+1}$

abzuändern. Dann lauten die ersten Folgenglieder 1, 1/2, 1/3, 1/4, … In gleicher Weise kann man eine Funktionsvorschrift für beliebige Exponenten aufstellen:

Geometrische Folgen

→ Hauptartikel: Geometrische Folge

Die geometrische Folge

So wie in einer arithmetischen Folge aufeinanderfolgende Glieder eine konstante Differenz haben, so stehen in einer geometrischen Folge

$a_i = a_0 \cdot q^i$

aufeinanderfolgende Glieder in einem konstanten Verhältnis zueinander, $a_{i+1} / a_i = q$ . Zum Beispiel ergibt sich mit q=2 und a_0 = 1 die Folge der Zweierpotenzen

also zum Beispiel für die ersten zehn Glieder die Folge 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024 (jedes Glied ist doppelt so groß wie das vorangegangene). Wichtig ist diese Folge speziell für die Umwandlung von den in der Informatik verwendeten Dualzahlen in Dezimalzahlen (und umgekehrt). Eine geometrische Folge mit $\vert q \vert < 1$ konvergiert gegen Null, wie beispielsweise die Folge 1; 0,1; 0,01; … zu q = 0{,}1 :

$a_i = \left(\frac{1}{10}\right)^i.$

Wenn q=1 erhält man die triviale Folge 1, 1, 1, …; wenn q=-1 , erhält man aus

die fundamentale alternierende Folge 1, −1, 1, −1, …

Ein Beispiel für die Alltagsanwendung der geometrischen Folge ist die gleichstufige Stimmung der musikalischen Tonleiter – die aufeinanderfolgenden Glieder, hier Halbtonschritte, besitzen zueinander ein konstantes Frequenzverhältnis.

Verallgemeinerungen

In der Topologie ist ein Netz eine Verallgemeinerung einer Folge.

Ebenso wie bei Funktionen kann man neben den hier definierten Folgen mit Werten in Mengen auch Folgen mit Werten in einer echten Klasse definieren, also beispielsweise Folgen von Mengen oder Gruppen.

Folgenräume

Aus Folgen können die Folgenräume gebildet werden, die vor allem in der Funktionalanalysis zur Konstruktion von Beispielen herangezogen werden.

Literatur

Harro Heuser: Lehrbuch der Analysis, Teil 1, Teubner Verlag, Stuttgart

Basierend auf einem Artikel in:

Wikipedia.de