Rechteckschwingung

Das Rechtecksignal bzw. die Rechteckschwingung bezeichnet ein periodisches Signal, das zwischen zwei Werten hin und her schaltet und in einem Diagramm über der Zeit einen rechteckigen Verlauf aufweist. Es kann unipolar oder bipolar auftreten.

Gegenüberstellung der elementaren Schwingungsformen

Das Rechtecksignal gehört bei der Klangerzeugung in Synthesizern zu den Grundformen und weist einen „hohlen“ Klangcharakter auf, weil allein ungerade ganzzahlige Vielfache einer Grundfrequenz erzeugt werden, die man Harmonische nennt, weshalb es häufig als Basis zur Nachahmung von Flöten und Blechblasinstrumenten dient.

Signale mit ideal rechteckigem Verlauf existieren nur theoretisch. Die Flanken können nicht senkrecht ansteigen und somit einen unendlich steilen Sprung ausführen; den stattdessen realen Sprung beschreiben die Anstiegs- und Abfallzeiten. Unter anderem wegen des kapazitivem und induktiven Verhaltens der Übertragungsleitungen weist ein Rechtecksignal häufig auch ein Unter- und Überschwingen auf.

Der Tastgrad ist für die Betrachtung als Digitalsignal unbedeutend; er beeinflusst aber den Gleichwert und den Anteil der Harmonischen.

Erzeugung

Ein rechteckförmiges Signal erzeugt man entweder mit einem astabilen Multivibrator, allgemein mit einem Rechteckgenerator, oder aus einer anderen Signalform mittels eines Schmitt-Triggers.

Ein zusätzlich zeitlich symmetrisches Signal erhält man bei stabiler Frequenz durch Frequenzhalbierung. Bei Übertragung als Wechselspannung (also ohne einen Gleichanteil) ist eine zeitlich symmetrische Rechteckspannung auch in der Spannungshöhe symmetrisch.

Auch Quarzoszillatoren geben meistens eine Rechteckschwingung ab, die zum Beispiel als Taktsignal für einen Mikroprozessor verwendet wird. Der Schwingquarz selbst führt dabei jedoch eine Sinusschwingung aus.

Davon abweichende Formen (zum Beispiel für Messzwecke) werden heute mit Funktionsgeneratoren mittels direkter digitaler Synthese (DDS) erzeugt.

Eigenschaften

Rechtecksignale sind durch folgende Eigenschaften charakterisiert:

Frequenz bzw. Periodendauer
Tastgrad: Er beträgt bei einer symmetrischen Rechteckschwingung 50 % und kann sonst im Bereich zwischen 0 und 100 % liegen.
Anstiegs- und Abfallzeit: Rechteckschwingungen mit hoher Flankensteilheit enthalten besonders viele Oberschwingungen (siehe unten Fourieranalyse)
Low- und High-Pegel (zum Beispiel unipolar mit 0 und 5 Volt bei TTL-Schaltungen)

Eine weitere Eigenschaft in der Digitaltechnik ist das Jitter, d.h. die zwischen den Impulsen auftretenden Zeitabweichungen bzw. die Frequenzkonstanz.

Verwendung

Rechtecksignale sind die Grundlage der digitalen Signalverarbeitung. Rechteckschwingungen (d.h. periodische Rechtecksignale) treten u.a. auf:

als Taktsignal für digitale Prozessoren und Controller
als pulsweitenmoduliertes Signal bei Sensoren, Digital-Analog- und Analog-Digital-Umsetzern, Schaltreglern und Schaltnetzteilen sowie Klasse-D-Audioverstärkern
als Testsignal an Oszilloskopen zum Abgleich der Frequenzkompensation der angeschlossenen Messspitzen
am Ausgang von Impuls- und Funktionsgeneratoren für Laborzwecke
in Synthesizern als eine der Grundschwingungsformen, häufig mit einstellbarer Pulsweitenmodulation
als einfaches, digital erzeugbares Tonsignal (z.B. Signaltöne bei Geräten, Kinderspielzeug)

Spektrale Betrachtung

Die Rechteckschwingung mit einer einzigen Frequenz kann auch als Überlagerung von Sinusschwingungen mit unendlich vielen Frequenzen angesehen werden.

Fourieranalyse

Die Fourieranalyse ermöglicht durch Anwendung mathematischer Verfahren die Zerlegung eines Signals in Sinus- und Kosinusfunktionen. Unter der Voraussetzung eines idealen und symmetrischen Rechtecksignals ohne Gleichanteil ergibt sich folgende Fourierreihe:

$f(t)={\frac {4h}{\pi }}\left[\sin(\omega t)+{\frac {1}{3}}\sin(3\omega t)+{\frac {1}{5}}\sin(5\omega t)+\ldots \right]={\frac {4h}{\pi }}\sum _{k=1}^{\infty }{\frac {\sin((2k-1)\omega t)}{2k-1}}$

mit dem Scheitelwert der Rechteckschwingung, deren Grundfrequenz bzw. Grund-Kreisfrequenz $\omega=2\pi f$ und der Zeit . Die Formel zeigt, dass das Frequenzspektrum eines symmetrischen Rechtecksignals ausschließlich aus ungeradzahligen Harmonischen besteht, die sich auch mit einem Spektrumanalysator messen lassen. Die Amplituden der Oberschwingungen nehmen mit steigender Frequenz ab.

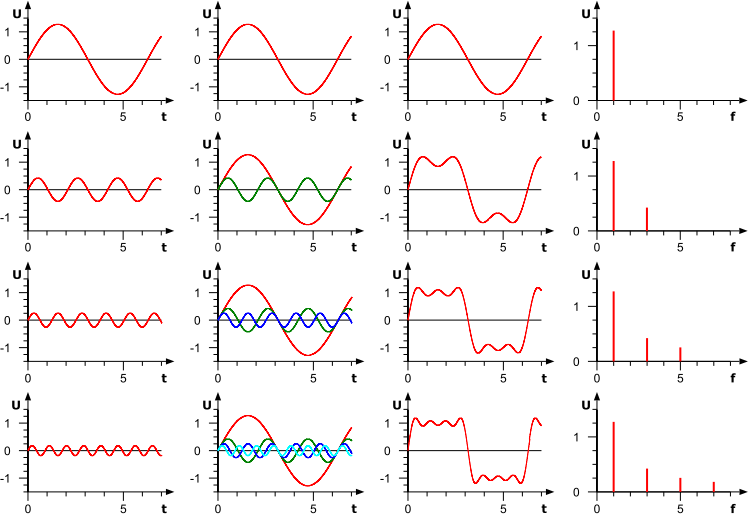
Fouriersynthese

Gibbssches Phänomen bei einer Rechteckschwingung

Wird nun der Prozess umgekehrt und eine Fouriersynthese ausgeführt, dann ist das Resultat jedoch kein ideales Rechtecksignal.

Die Fourierreihenentwicklung führt vielmehr zu einer Signalform, bei der das Signal vor und hinter den Sprungstellen unter das untere (gedachte) Impulsdach taucht und über das obere (gedachte) Impulsdach hinausschießt.

Diese Erscheinung wird als Gibbssches Phänomen bezeichnet und darf nicht mit dem bereits erwähnten Unter- und Überschwingen verwechselt werden, wird aber dennoch oft ebenso bezeichnet.

Das Fehlen der in der Praxis nicht übertragbaren hohen Frequenzanteile bedingt die Verrundung an den Sprungstellen. Eine Welligkeit im Impulsdach wird davon kaum verursacht.

Demonstration zur Erzeugung einer Rechteckschwingung durch Überlagerung von Sinusschwingungen (Fouriersynthese)

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de