Kreisfrequenz
| Physikalische Größe | |||||||
|---|---|---|---|---|---|---|---|
| Name | Kreisfrequenz, Winkelfrequenz | ||||||
| Formelzeichen | |||||||
| Abgeleitet von | Frequenz | ||||||
| |||||||
Die Kreisfrequenz oder Winkelfrequenz ist
eine physikalische Größe der Schwingungslehre. Als
Formelzeichen wird der
griechische Buchstabe
(kleines Omega)
verwendet. Sie ist ein Maß dafür, wie schnell eine Schwingung abläuft. Im
Gegensatz zur Frequenz
gibt sie aber nicht die Anzahl der Schwingungsperioden
bezogen auf eine Zeitspanne
an, sondern den überstrichenen Phasenwinkel
der Schwingung pro Zeitspanne. Da eine Schwingungsperiode einem Phasenwinkel von
entspricht, unterscheidet sich die Kreisfrequenz von der Frequenz durch einen
Faktor
:
,
wobei
die Periodendauer
der Schwingung ist. Die Einheit der Kreisfrequenz ist
.
Anders als bei der Frequenz wird diese Einheit bei der Kreisfrequenz
nicht als Hertz
bezeichnet.
Zeigermodell
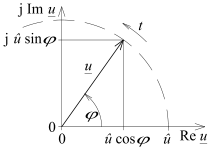
Harmonische Schwingungen lassen sich durch die Rotation eines Zeigers darstellen, dessen Länge der Amplitude der Schwingung entspricht. Die Momentanauslenkung ist dabei die Projektion des Zeigers auf eine der Koordinatenachsen. Wenn man für die Darstellung des Zeigers die komplexe Zahlenebene verwendet, entspricht – je nach Definition – entweder der Realteil oder der Imaginärteil der Momentanauslenkung.
Die Kreisfrequenz
ist die Änderungsrate
des Phasenwinkels
des rotierenden Zeigers (siehe nebenstehendes Bild). In
Anpassung an die Einheit der Kreisfrequenz sollte der Winkel hierbei in Bogenmaß
angegeben werden.
Das Zeigermodell ist auf alle Arten von Schwingungen (mechanisch, elektrisch
etc.) und Signalen anwendbar. Da eine Schwingungsperiode
einer vollen Umdrehung des Zeigers entspricht und der Vollwinkel
beträgt, ist die Kreisfrequenz einer harmonischen Schwingung immer das
-fache
ihrer Frequenz. Häufig wird die Angabe der Kreisfrequenz gegenüber der Frequenz
bevorzugt, da viele Formeln der Schwingungslehre sich aufgrund des Auftretens trigonometrischer
Funktionen, deren Periode per Definition
ist, mit Hilfe der Kreisfrequenz kompakter darstellen lassen: z. B. bei einer
einfachen Cosinus-Schwingung:
statt
.
Im Falle zeitlich nicht konstanter Kreisfrequenzen wird auch der Begriff momentane Kreisfrequenz verwendet.
Verwendung in der Schwingungslehre
Eine harmonische
Schwingung lässt sich allgemein als Funktion der Kreisfrequenz
beschreiben:
Sie kann, wie in der Elektrotechnik üblich, durch den Real- und Imaginärteil
eines mit konstanter Winkelgeschwindigkeit
rotierenden komplexen Zeigers
in der gaußschen
Zahlenebene als Funktion der Kreisfrequenz und der Zeit dargestellt
werden.
Der zeitabhängige Winkel
des komplexen Zeigers wird dabei als Phasenwinkel
bezeichnet.
Der Zusammenhang mit Sinus und Kosinus ergibt sich aus der Eulerschen Formel.
Kennkreisfrequenz und Eigenkreisfrequenz
Schwingfähige Systeme werden durch die Kennkreisfrequenz und die
Eigenkreisfrequenz beschrieben. Ein ungedämpftes frei schwingendes System
schwingt mit seiner Kennkreisfrequenz ,
ein gedämpftes System ohne äußere Anregung schwingt mit seiner
Eigenkreisfrequenz
.
Die Eigenkreisfrequenz eines gedämpften Systems ist stets kleiner als die
Kennkreisfrequenz. Die Kennkreisfrequenz wird in der Mechanik auch als
ungedämpfte Eigenkreisfrequenz bezeichnet.
Für das Beispiel eines elektrischen
Schwingkreises gilt mit dem Widerstand ,
der Induktivität
und der Kapazität
für die Kennkreisfrequenz:
Für ein Federpendel
mit der Federsteifigkeit
und der Masse
gilt für die Kennkreisfrequenz:
und mit der Abklingkonstante
bzw.
für die Eigenkreisfrequenz:
.
Weitere Beispiele siehe Fadenpendel.
Komplexe Kreisfrequenz
Aus der komplexen Zeigerdarstellung einer harmonischen Schwingung
ergibt sich mit dem üblichen Ansatz
die Verallgemeinerung zur komplexen Kreisfrequenz
mit dem Realteil
und der Kreisfrequenz
.
Durch die komplexe Kreisfrequenz
kann nicht nur eine konstante harmonische Schwingung mit
dargestellt werden, sondern auch eine gedämpfte Schwingung mit
und eine angeregte Schwingung mit
.
Eine klassische Anwendung der komplexen Kreisfrequenz ist die erweiterte
symbolische Methode der Wechselstromtechnik.
Eine gedämpfte Schwingung kann wie folgt mit der konstanten komplexen Kreisfrequenz s als komplexer Zeiger dargestellt werden:
Dabei ist
die Eigenkreisfrequenz des schwingfähigen Systems und
ist gleich dem negativen Wert der Abklingkonstante:
(siehe dazu den vorhergehenden Abschnitt).
Bei der Laplacetransformation
hat die komplexe Kreisfrequenz
eine allgemeinere Bedeutung als Variable im Bildbereich der Transformation
zur Darstellung beliebiger Zeitfunktionen und Übertragungsfunktionen in der
komplexen Frequenzebene („s-Ebene“).
Beziehung zur Winkelgeschwindigkeit
Häufig wird der Begriff „Kreisfrequenz“ durch eine mechanische Analogie eingeführt: Wenn man einen Punkt eines rotierenden Körpers (oder einen rotierenden Vektor) senkrecht zur Drehachse auf eine Ebene projiziert, erhält man die Abbildung einer harmonischen (sinusförmigen) Schwingung. Die Kreisfrequenz der Schwingung, die sich aus dieser Projektion ergibt, hat dabei denselben Zahlenwert wie die Winkelgeschwindigkeit des rotierenden Körpers. Diese Projektion ist jedoch lediglich die mechanische Veranschaulichung eines abstrakten Konzepts: Harmonische (d.h. sinusförmige) Schwingungen werden in der komplexen Ebene durch die Rotation eines komplexen Zeigers dargestellt. Durch diese Abstraktion ist der Begriff Kreisfrequenz auf Schwingungen jeder Art (elektrisch, mechanisch etc.) anwendbar und hat keinen direkten Bezug zu rotierenden Körpern. Die Kreisfrequenz beschreibt die abstrakte Änderungsrate des Phasenwinkels in der komplexen Ebene, während die Winkelgeschwindigkeit die Änderung eines physikalischen Winkels an einem physikalischen Körper pro Änderung der Zeit beschreibt.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 30.05. 2021
