Laplace-Transformation
Die Laplace-Transformation, benannt nach Pierre-Simon
Laplace, ist eine einseitige Integraltransformation,
die eine gegebene Funktion
vom reellen Zeitbereich
in eine Funktion
im komplexen Spektralbereich (Frequenzbereich;
Bildbereich)
überführt. Diese Funktion
wird Laplace-Transformierte oder Spektralfunktion genannt.
Die Laplace-Transformation hat Gemeinsamkeiten mit der Fourier-Transformation: So gibt es zur Laplace-Transformation ebenfalls eine inverse Transformation, die auch Bromwich-Integral genannt wird.
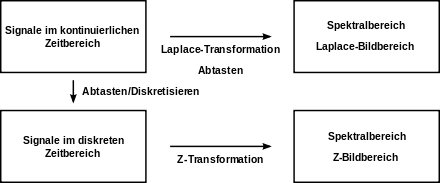
Die Laplace-Transformation gilt für Signale im kontinuierlichen Zeitbereich. Sie ist verwandt mit einer entsprechenden Transformation für Signale im diskreten Zeitbereich: der Z-Transformation.
Allgemeines
Die Laplace-Transformation und deren Inversion sind Verfahren zur Lösung von Problemstellungen der mathematischen Physik und der theoretischen Elektrotechnik, welche mathematisch durch lineare Anfangs- und Randwertprobleme beschrieben werden. Die Laplace-Transformation gehört zur Klasse der Funktionaltransformationen, spezieller zu den Integraltransformationen, und ist eng verwandt mit der Fourier-Transformation. Die Motivation, die Fourier-Transformation weiter zur Laplace-Transformation zu entwickeln, liegt in der beschränkten Klasse von Funktionen, für welche im Rahmen der Fourier-Transformation das Fourier-Integral existiert.
Um die Konvergenz für einen größeren Umfang von Funktionen bei der
Laplace-Transformation zu sichern, erweitert man die Integration des
Fourier-Integrals um den Faktor ,
der für σ > 0 und
gegen 0 geht und so für hinreichend große t die Konvergenz sicherstellt. Damit
geht der Frequenzparameter der Fourier-Transformation
in den komplexen
Frequenzparameter
über. (
ist die imaginäre
Einheit mit
.
In der Elektrotechnik ist
statt
gebräuchlich, da dort
für den elektrischen Wechselstrom steht.) Im Gegensatz zu der zweiseitigen
Laplace-Transformation und auch der Fourier-Transformation ist die
gewöhnliche, einseitige Laplace-Transformation nur für positive Werte von t ≥
0 definiert. Diese Einschränkung ist deswegen zulässig, da im Rahmen der Systemtheorie
und Anwendung im Bereich der Physik
und Technik
nur real existierende kausale
Systeme eine Rolle spielen. Bei der theoretischen Untersuchung nichtkausaler
Systeme ist die zweiseitige Laplace-Transformation nötig.
Die Laplace-Transformation bildet Originalfunktionen einer reellen Veränderlichen auf Bildfunktionen einer komplexen Veränderlichen ab. Bei Existenz der Laplace-Transformation entspricht die Differentiation und Integration im reellen Originalbereich einer einfachen algebraischen Operation im Bildbereich, was die praktische Bedeutung begründet. Bei vielen Anfangs- und Randwertproblemen spielt der Zeitbereich die Rolle des reellen Originalbereiches und der Frequenzbereich oder Spektralbereich diejenige des komplexen Bildbereiches.
Die Untersuchung der Bildfunktion liefert häufig wesentlich bessere physikalische Einblicke in das Verhalten linearer Systeme gegenüber Studien im Zeitbereich. Vor allem das Resonanzverhalten physikalischer Systeme kann im Frequenzbereich einfacher beschrieben werden. Aufgrund der besseren Konvergenz gegenüber der Fourier-Transformation können beispielsweise Übertragungsfunktionen auch dann noch analysiert werden, wenn sich ein lineares System instabil verhält.
Bei zeitdiskreten Systemen wird, um die Periodizität in der s-Ebene zu vermeiden (diese ist bedingt durch die zeitlich diskreten Abtastwerte im Rahmen der diskreten Laplace-Transformation) eine konforme, nichtlineare Abbildung auf die sogenannte z-Ebene durchgeführt, was zu der Z-Transformation führt.
Geschichte
Die ersten Hinweise auf die Idee der Laplace-Transformation finden sich bereits in den Arbeiten des Basler Mathematikers und Physikers Leonhard Euler (1707–1783, Institutiones calculi integralis, vol. 2, 1768). Benannt wird die Laplace-Transformation nach dem französischen Mathematiker und Astronomen Pierre-Simon Laplace (1749–1827), der die Transformation 1782 im Rahmen von Wahrscheinlichkeitsstudien einführte. Tatsächlich war der ungarische Mathematiker József Miksa Petzval (1807–1891) der erste, der sie systematisch untersuchte, wohingegen Laplace sie nur zur Lösung seiner Probleme anwandte. Jedoch fand das Werk von Petzval keine Beachtung, unter anderem, weil ihn einer seiner Studenten zu Unrecht des Plagiats an Laplace bezichtigt hatte.
Ungefähr hundert Jahre später wandte der britische Elektroingenieur und Physiker Oliver Heaviside (1850–1925) die von ihm durch Probieren gefundene Operatorenrechnung zur Lösung von Differentialgleichungen in der theoretischen Elektrotechnik an. Der deutsche Mathematiker Gustav Doetsch (1892–1977) ersetzte diese durch die Laplace-Transformation, erarbeitete deren mathematische Grundlagen und führte die Laplace-Transformation einer breiten Anwendung zur Lösung vieler Problemstellungen der mathematischen Physik und der theoretischen Elektrotechnik zu, welche durch lineare Anfangs- und Randwertprobleme beschrieben werden. Mindestens seit Anfang der 60er-Jahre des 20. Jahrhunderts finden sich Theorie und Anwendung der Laplace-Transformation in Lehrbüchern und Lehrplänen der theoretischen Elektrotechnik und vor allem in Büchern über gewöhnliche und partielle Differentialgleichungen.
Eine rein algebraische Begründung und Erweiterung der Operatorenrechnung von Heaviside führte der polnische Mathematiker Jan Mikusiński (1913–1987) durch, ohne die Laplace-Transformation zu benutzen. Diese Erweiterung erfasst auch Funktionen, die keine Laplace-Transformierte besitzen, und liefert beispielsweise eine einfache exakte Begründung für die Deltafunktion ohne Heranziehung von Distributionen.
Definition
Sei
eine Funktion. Die Laplace-Transformation von
ist durch
definiert, insofern das Integral existiert. Es handelt sich um ein (uneigentliches)
Parameterintegral
mit dem Parameter .
Die Exponentialfunktion
ist der Kern
der Laplace-Transformation. Die Funktion
wird Laplace-Transformierte der Funktion
genannt.
Existenz
Eine Funktion
heißt von exponentieller Ordnung, wenn es positive Konstanten
,
und eine Stelle
mit
gibt, so dass
für
gilt. Manchmal wird auch die strengere Bedingung
statt
benutzt.
Wenn
von exponentieller Ordnung ist und damit die Größen
,
,
aus obiger Gleichung gegeben sind, und wenn zusätzlich
gilt, so existiert in der Halbebene
das Laplace-Integral
.
Die Bedingung
ist bereits erfüllt, wenn die Funktion
in
stückweise stetig ist.
Beispiele für Funktionen, deren Laplace-Integral existiert, sind in den Korrespondenztabellen weiter unten aufgelistet.
Die genannten Bedingungen sind nur hinreichend für die Existenz des Laplace-Integrals. Wenn sie nicht erfüllt werden, muss man weitere Untersuchungen anstellen.
Einige Beispiele:
- Die Funktion
ist zwar von exponentieller Ordnung (man setze
,
,
). Das Integral in (2) ist für jedes
jedoch divergent. Diese Funktion besitzt in der Tat keine Laplace-Transformierte.
- Die Funktion
ist zwar stückweise stetig (sogar stetig), aber nicht von exponentieller Ordnung. Diese Funktion besitzt ebenfalls keine Laplace-Transformierte.
- Die Funktion
ist von exponentieller Ordnung (setze
,
,
), zudem existiert das Integral
(mit dem Wert
). Das Laplace-Integral existiert und ist gleich
.
Laplace-Rücktransformation
Zur Laplace-Transformation gibt es auch eine Rücktransformation, also einen
Operator der zu einer gegebenen Spektralfunktion
die entsprechende Zeitfunktion
zuordnet. Dieser Integraloperator wird auch Bromwich-Integral genannt und ist
nach dem Mathematiker und Physiker Thomas
John I’Anson Bromwich benannt.
Aussage
Die Zeitfunktion
kann durch die Umkehrformel
aus der Spektralfunktion
bestimmt werden, dabei ist
der größte Realteil einer Singularität von
.
Beispiel
Bekannte Rücktransformationen sind in der Literatur in Korrespondenztabellen zusammengefasst. In der Praxis muss daher die Spektralfunktion meist nur auf diese tabellierten Fälle zurückgeführt werden, z.B. durch Partialbruchzerlegung.
Als Beispiel sei die Rücktransformation gebrochen rationaler Funktionen betrachtet: Für die Spektralfunktion
lässt sich mit der (tabellierten, hier exemplarisch berechneten) Korrespondenz
die Rücktransformierte direkt angeben als
Im Fall komplex konjugierter Pole sind Vereinfachungen von
durch Anwendung trigonometrischer Identitäten möglich.
Wichtige Anwendungen
Allgemein bietet sich die Laplace-Transformation zur Lösung von linearen
Differentialgleichungen bzw. Differentialgleichungssystemen mit konstanten
Koeffizienten an. Der Vorteil ist hierbei die Algebraisierung: Ableitungen im
Bildbereich entstehen als Produkt aus Laplace-Transformierter der
Originalfunktion und dem Laplace-Faktor .
Diese bewirkt, dass
- gewöhnliche Differentialgleichungen im Originalbereich auf algebraische Gleichungen im Bildbereich,
- partielle Differentialgleichungen mit
unabhängigen Variablen im Originalbereich auf partielle (bzw. gewöhnliche) Differentialgleichungen mit
unabhängigen Variablen im Bildbereich,
- und Integralgleichungen vom Faltungstyp im Originalbereich auf algebraische Gleichungen im Bildbereich
abgebildet werden. Die Lösungen der transformierten Probleme lassen sich im Bildbereich wesentlich einfacher erarbeiten als im Originalbereich. In Sonderfällen können auch lineare Differentialgleichungen mit Polynomkoeffizienten so gelöst werden.
Besonders effizient eignet sich die Laplace-Transformation dazu, Anfangswertprobleme
zu lösen, da die Anfangswerte in die Bildgleichung eingehen. Man transformiert
die Differentialgleichung in den Spektralbereich, löst die so erhaltene
algebraische Gleichung und transformiert die Lösung in den Zeitbereich zurück. An
dieser Stelle sei noch einmal darauf hingewiesen, dass das gewonnene Ergebnis
ausschließlich Aussagen für den Zeitraum ab
liefert, da die Laplace-Transformierte durch die Integration ab
bestimmt wird.
Der Nachteil ist die im Allgemeinen meist komplizierte Rücktransformation.
In Maschinenbau und Elektrotechnik, speziell
in der Regelungstechnik
spielt die Laplace-Transformation vor allem aufgrund des Faltungssatzes eine große
Rolle. Da das Verhalten des Systemausgangs sich im Spektralbereich als Produkt
der Eingangsfunktion und einer dem System eigenen, von der jeweiligen Anregung
unabhängigen Übertragungsfunktion
darstellen lässt, lassen sich viele Systemeigenschaften durch Untersuchung der
Übertragungsfunktion bestimmen (die man wiederum durch einfache Verknüpfungen
elementarer Übertragungsfunktionen erhält), ohne eine explizite Lösung der
System-Differentialgleichung, beispielsweise durch Rücktransformation, zu
bestimmen. Elegant möglich ist dadurch beispielsweise die Stabilitätsanalyse
linearer zeitinvarianter Systeme und Analyse des Schwingungsverhaltens
(Dämpfung), der Schnelligkeit sowohl von Regelstrecken als auch von
geschlossenen Regelkreisen. Da die Übertragungsfunktion im Laplace-Bereich für
in eine Übertragungsfunktion im Fourier-Bereich übergeht, lassen sich zu guter
Letzt auch graphische Darstellungen des Übertragungsverhaltens, sprich
Amplituden- und Phasenfrequenzgänge (Bode-Diagramme)
gewinnen.
Eigenschaften
Grenzwertsätze
Insbesondere strebt jede Laplace-Transformierte gegen ,
wenn
gegen
strebt. Der erste Grenzwertsatz gilt nur, wenn
außer einem einfachen Pol bei
keine weiteren Singularitäten
in der Halbebene
besitzt.
Eindeutigkeit
Wenn für zwei Zeitfunktionen
und
die Voraussetzungen gelten:
und
sind stückweise stetig
und
sind von exponentieller Ordnung für
- die Laplace-Transformierten
und
existieren
im Konvergenzbereich
dann ist
überall dort, wo
und
stetig sind.
Beziehung zur Fourier-Transformation
Die Laplace-Transformation ist eine ähnliche Integraltransformation wie die
Fourier-Transformation.
Setzt man
mit reellem
,
so entsteht der Sonderfall
Diese Integraltransformation wird manchmal auch einseitige Fourier-Transformation genannt.
Analytische Eigenschaften
Analytizität
Die Laplace-Transformierte ist infolge der Existenz ihrer Ableitungen nach
der komplexen Frequenz
im Bildbereich
im Innern der Konvergenzhalbebene beliebig oft komplex differenzierbar, das
heißt analytisch
(beziehungsweise regulär oder holomorph).
Somit kann
mit den Mitteln der Funktionentheorie
untersucht werden. Die Funktion
kann in die linke Halbebene analytisch fortsetzbar sein, aber nicht zwingend.
Eine solche analytische Fortsetzung lässt sich dann aber nicht mehr als
Laplace-Transformierte schreiben.
Konjugierte Symmetrie
Eine weitere wichtige Eigenschaft der Laplace-Transformierten reeller Zeitfunktionen ist die konjugierte Symmetrie im komplexen Bildbereich
oder separiert in Real- und Imaginärteil
wobei der Überstrich die komplex konjugierte Größe kennzeichnet. Aufgrund
dieser Eigenschaft genügt es, die Bildfunktion in der oberen Halbebene
zu studieren.
Endliche Laplace-Transformation
Die Laplace-Transformation bildet eine endliche Zeitfunktion
für
auf eine ganze Funktion ab. Dies bedeutet, dass die Bildfunktion
in der ganzen komplexen Frequenzebene analytisch ist, also keine Singularitäten besitzt.
Physikalische Dimension
Bei Anwendungen der Laplace-Transformation ist auch die Dimension der Laplace-Transformierten
von Interesse. Meist hat
die Dimension
,
dann besitzt die komplexe Frequenz
die Dimension
.
Der Ausdruck
im Integranden ist somit dimensionslos. Durch die Integration über den
Zeitbereich wird die Dimension der Zeitfunktion
mit der Dimension des Zeitdifferentials
multipliziert:
.
Beispielsweise besitzt die Laplace-Transformierte eines elektrischen Stroms
(gemessen in Ampere)
die Dimension einer Ladung As = C, also Coulomb.
Korrespondenztabellen
Allgemeine Eigenschaften
| Allgemeine Eigenschaft bzw. Operation |
Originalfunktion |
Bildfunktion |
|---|---|---|
| Linearität | ||
| Ähnlichkeitssatz | ||
| Verschiebung im Originalbereich (bei einseitiger Transformation nur
|
||
| Verschiebung im Bildbereich (Dämpfungssatz) | ||
| Komplexe Konjugation | ||
| Zeitspiegelung (bei einseitiger Transformation nicht anwendbar!) | ||
| Zeitdehnung ( |
||
| Sinus-Multiplikation | ||
| Cosinus-Multiplikation | ||
| 1. Ableitung im Originalbereich | ||
| 2. Ableitung im Originalbereich | ||
| 1. Ableitung im Bildbereich | ||
| 2. Ableitung im Bildbereich | ||
| Integration im Originalbereich | ||
| Integration im Bildbereich | ||
| Faltung
im Originalbereich Multiplikation im Bildbereich |
||
| Multiplikation im Originalbereich Faltung im Bildbereich |
konvergiert für | |
| Periodische Funktion |
Korrespondenztabelle
Für die Originalfunktion gilt
| Funktionsname | Originalfunktion |
Bildfunktion |
Konvergenz- bereich |
|---|---|---|---|
| Diracsche
Deltadistribution Einheitsimpuls |
|||
| Heavisidesche
Sprungfunktion Einheitssprung |
|||
| Exponentialfunktion | |||
| Exponentialverteilung | |||
| 1-te Potenz | |||
| n-te Potenz | |||
| Potenzreihe | |||
| Gedämpfte Potenzfunktion | |||
| n-te Wurzel | |||
| Sinus | |||
| Cosinus | |||
| Sinus hyperbolicus | |||
| Cosinus hyperbolicus | |||
| Logarithmus naturalis | |||
| Bessel-Funktion erster Art der Ordnung 0 |
|||
| Modifizierte
Bessel-Funktion erster Art der Ordnung 0 |
|||
| Bessel-Funktion erster Art der Ordnung n |
|||
| Modifizierte
Bessel-Funktion erster Art der Ordnung n |
|||
| Laguerre-Polynome der Ordnung n |
Beispiel
Im Folgenden ist die Lösung des Anfangswertproblems einer gewöhnlichen Differentialgleichung erster Ordnung mit konstanten Koeffizienten mit Hilfe der Laplace-Transformation dargestellt:
mit .
Unter Ausnutzung der Linearität der Laplace-Transformation und des Verhaltens
bei Ableitung im Ursprungsbereich (s. Tabelle der allgemeinen Eigenschaften) ist
die Transformierte gegeben durch
mit .
Die Rücktransformation in den Ursprungsbereich ist in obiger
Korrespondenztabelle aufgeführt (s. Exponentialfunktion),
Obige Differentialgleichung beschreibt also einfache Wachstums- und Abnahmeprozesse und findet sich demnach in vielen Bereichen, u.a. in Natur-, Wirtschafts- und Sozialwissenschaften.
Laplace-Transformation für Maße
Die Laplace-Transformation wird auch in der Wahrscheinlichkeitstheorie
und der Maßtheorie
als Transformation von Wahrscheinlichkeitsmaßen
und von Maßen
verwendet. Für ein endliches
Maß
auf
wird die Laplace-Transformation dabei definiert als
,
wobei
ist.
Für ein zufälliges
Maß
wird die Laplace-Transformierte definiert als
für positive, reellwertige messbare
Funktionen .
Literatur
- Lothar Berg: Operatorenrechnung. Band 2: Funktionentheoretische Methoden. VEB Deutscher Verlag der Wissenschaften, Berlin 1974.
- William E. Boyce, Richard C. DiPrima: Gewöhnliche Differentialgleichungen. Einführung, Aufgaben, Lösungen. Spektrum – Akademischer Verlag, Heidelberg u. a. 1995, ISBN 3-86025-151-1.
- Hans Jörg Dirschmid: Mathematische Grundlagen der Elektrotechnik. 2., durchgesehene Auflage. Vieweg, Braunschweig u. a. 1987, ISBN 3-528-13034-2.
- Otto Föllinger: Laplace-, Fourier- und z-Transformation. Bearbeitet von Mathias Kluwe. 8., überarbeitete Auflage. Hüthig, Heidelberg 2003, ISBN 3-7785-2911-0.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 21.05. 2021