
Logarithmus

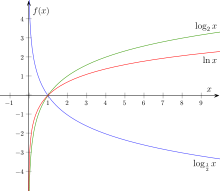
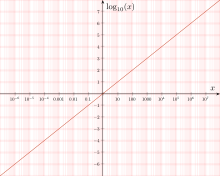
Als Logarithmus (Plural: Logarithmen; von altgriechisch λόγος lógos, „Verständnis, Lehre, Verhältnis“, und ἀριθμός, arithmós, „Zahl“) einer Zahl bezeichnet man den Exponenten, mit dem eine vorher festgelegte Zahl, die Basis, potenziert werden muss, um die gegebene Zahl, den Numerus, zu erhalten. Logarithmen sind nur für positive reelle Zahlen definiert, auch die Basis muss positiv sein.
Der Logarithmus einer positiven reellen Zahl
zur Basis
ist also der Wert des Exponenten, wenn
als Potenz
zur Basis
dargestellt wird, also diejenige Zahl
,
welche die Gleichung
löst. Man schreibt
;
weitere Notationen siehe Bezeichnungen.
Das Logarithmieren, d.h. der Übergang von
zu
,
ist damit eine Umkehroperation
des Potenzierens.
Die Funktion, die bei gegebener fester Basis
jeder positiven Zahl ihren Logarithmus zuordnet, nennt man
Logarithmusfunktion zur Basis
.
Mit Logarithmen lassen sich sehr stark wachsende Zahlenreihen übersichtlich
darstellen, da der Logarithmus für große Zahlen viel langsamer steigt als die
Zahlen selbst. Wie die Gleichung
zeigt, kann man durch Logarithmieren eine Multiplikation durch die viel weniger
rechenintensive Addition ersetzen. Auch beschreiben Logarithmen auf mathematisch
elegante Weise viele technische Prozesse sowie Phänomene der Natur wie etwa das
Verhalten einer Halbleiter-Diode,
die Spirale eines Schneckenhauses
oder die Wahrnehmung
unterschiedlicher Lautstärken durch das menschliche Ohr.
Entsprechende mathematische Berechnungen sind bereits aus der Zeit vor Christi Geburt aus Indien überliefert. Der Begriff Logarithmus wurde von John Napier im frühen 17. Jahrhundert geprägt. Napier zu Ehren wird der Natürliche Logarithmus (s. u.) manchmal auch Napierscher Logarithmus oder Neperscher Logarithmus genannt.
Überblick
Die Verwendung des Logarithmus lässt sich bis in die indische Antike zurückverfolgen. Mit dem aufstrebenden Bankwesen und dem Fortschritt der Astronomie im Europa des 17. Jahrhunderts erlangte der Logarithmus immer mehr Bedeutung. Seine Funktionswerte wurden in Tabellenwerken, den Logarithmentafeln, erfasst, um sie nachschlagen zu können und nicht immer neu berechnen zu müssen. Diese Tabellen wurden schließlich durch Rechenschieber und später durch Taschenrechner verdrängt. Der Wechsel von den Tabellen zum Rechenschieber erfolgte in deutschen Schulen in den 1960er Jahren, der Wechsel zu Taschenrechnern ab den 1970er Jahren.
Zentrale Aspekte des Lebens lassen sich mit Hilfe von Logarithmen beschreiben. So nimmt zum Beispiel die Stärke eines Sinneseindrucks in Abhängigkeit von einer physikalischen Größe wie Helligkeit oder Lautstärke entsprechend dem Verlauf einer Logarithmusfunktion zu. Gleiches gilt für die wahrgenommene Tonhöhe in Abhängigkeit von der Frequenz eines Tones.
Logarithmen erlangten ihre historische Bedeutung durch den Zusammenhang
der es erlaubt, eine Multiplikation durch eine Addition auszudrücken.
Formal sind Logarithmen alle Lösungen
der Gleichung
zu vorgegebenen Größen
und
.
Je nachdem, über welchem Zahlenbereich und für welche Größen diese Gleichung betrachtet wird,
hat sie keine, mehrere oder genau eine Lösung. Ist die Lösung eindeutig, dann
wird sie als der Logarithmus von
zur Basis
bezeichnet und man schreibt
Beispielsweise ist der Logarithmus von 8 zur Basis 2 gleich 3, geschrieben
,
denn es ist
.
Falls die obige Gleichung nach
aufzulösen ist anstatt nach
,
so ist die Lösung gegeben durch die
-te
Wurzel
aus
.
Am bekanntesten und am weitesten verbreitet ist der Logarithmus über den positiven reellen Zahlen, der im Folgenden vornehmlich dargestellt wird.
Geschichte

Indische Mathematiker im 2. Jahrhundert v.Chr. haben als Erste Logarithmen erwähnt. Schon in der Antike nutzten sie Logarithmen zur Basis 2 für ihre Berechnungen. Im 8. Jahrhundert beschrieb der indische Mathematiker Virasena Logarithmen zur Basis 3 und 4. Ab dem 13. Jahrhundert wurden von arabischen Mathematikern ganze logarithmische Tabellenwerke erstellt.
Nicolas
Chuquet arbeitete klar die Rechengesetze für Potenzen
und
heraus durch eine gegenüberstellende Anordnung einer arithmetischen und einer
geometrischen Reihe.
Der deutsche Mathematiker Michael
Stifel formulierte ähnlich im Jahr 1544 die Beziehungen
und
neben anderen Autoren des 16. Jahrhunderts. Die Reduktion von
Multiplikation auf Addition steht neben trigonometrischen Additionsformeln am
Beginn der Entwicklung der Logarithmen.
Stifel ließ nur ganzzahlige Exponenten zu. John
Napiers (1550–1617) Idee war dagegen, einen stetigen Wertebereich für die
Exponenten zuzulassen.
Im 17. Jahrhundert entwickelte der Schweizer Uhrmacher Jost Bürgi (1552–1632) ein neues System zur Berechnung von Logarithmen, das er 1620 nach langer Arbeit veröffentlichte. Aber schon vorher, im Jahre 1614, veröffentlichte der schottische Denker John Napier ein Buch über Logarithmen, das ihn als „Erfinder der Logarithmen“ berühmt machte. Ihre Arbeiten und Erkenntnisse über Logarithmen entwickelten Bürgi und Napier jedoch unabhängig voneinander.
Das griechische Wort „Logarithmus“ bedeutet auf Deutsch „Verhältniszahl“ und
stammt von Napier. Es gilt nämlich: Genau dann steht
zu
im selben Verhältnis wie
zu
(als Formel:
),
wenn die Unterschiede ihrer Logarithmen übereinstimmen (als Formel:
).
Erstmals veröffentlicht wurden Logarithmen von diesem unter dem Titel
Mirifici logarithmorum canonis descriptio, was mit Beschreibung des
wunderbaren Kanons der Logarithmen übersetzt werden kann.
Nachdem der Oxforder Professor Henry Briggs (1561–1630) sich intensiv mit dieser Schrift beschäftigt hatte, nahm er mit ihrem Autor Kontakt auf und schlug vor, für die Logarithmen die Basis 10 zu verwenden (abgekürzt lg). Diese verbreiteten sich schnell und wurden besonders in der Astronomie geschätzt, was auch Pierre-Simon Laplace, im Vergleich zu den vorher benutzten trigonometrischen Tafeln, feststellte:
„L’invention des logarithmes, en réduisant le temps passé aux calculs de quelques mois à quelques jours, double pour ainsi dire la vie des astronomes.“
„Dadurch, dass die für Rechnungen benötigte Zeit von einigen Monaten auf einige Tage reduziert wurde, hat die Erfindung der Logarithmen sozusagen die Lebenszeit eines Astronomen verdoppelt.“
Wird die Eulersche
Zahl –
die im Jahre 1728 von Leonhard
Euler (1707–1783) bestimmt und erstmals 1742 veröffentlicht wurde – als
Basis des Logarithmus verwendet, so nennt man ihn den natürlichen
Logarithmus. Der natürliche Logarithmus wird dabei durch „ln“ abgekürzt.
Mit den Logarithmen war die mathematische Grundlage für die Weiterentwicklung des mechanischen Rechenschiebers gelegt; denn die Funktionsweise des Rechenschiebers basiert auf dem Prinzip der Addition und Subtraktion von Logarithmen.
Logarithmus in Anwendung und Natur

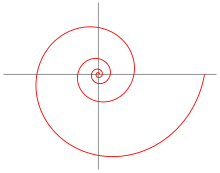

Anwendungen des Logarithmus finden sich vielfach in der Wissenschaft, wenn der Wertebereich viele Größenordnungen umfasst. Daten werden entweder mit einer logarithmischen Skala dargestellt, oder es werden logarithmisch definierte Größen verwendet, wie zum Beispiel beim pH-Wert oder bei der Empfindlichkeit der Sinnesorgane.
In der belebten Natur
In der belebten Natur finden sich zahlreiche Beispiele logarithmischer Spiralen, so z.B. das Wachstum von Schneckenhäusern oder die Anordnung der Kerne auf der Sonnenblume.
Schalldruckpegel
Der Schalldruckpegel wird als logarithmisches Maß zur Beschreibung der Stärke eines Schallereignisses verwendet. Dazu wird die Hilfsmaßeinheit Dezibel (dB) verwendet.
Helligkeitsempfindung
Auch für die Sinnesempfindung der Helligkeit hat sich eine logarithmische Bewertung bewährt (Weber-Fechner-Gesetz), da das menschliche Auge zwischen Dämmerung und hellem Sonnenschein bis zu 10,5 Zehnerpotenzen an physikalischer Leuchtdichte überbrücken kann.
pH-Wert
Der pH-Wert ist das Maß für den sauren oder basischen Charakter einer wässrigen Lösung. Anmerkung: In der Chemie werden logarithmische Skalen im Allgemeinen durch ein vorangestelltes p (für Potenz) gekennzeichnet, zum Beispiel beim pKs- oder pKb-Wert.
Richterskala
Die Richterskala, die zur Beschreibung von Erdbebenstärken genutzt wird, basiert auf einer deka-logarithmischen Einteilung. Die Erdbebenstärke steigt daher von Stufe zu Stufe exponentiell.
Sternhelligkeiten
Sternhelligkeiten werden in astronomischen Größenklassen angegeben, die ein logarithmisches Maß der tatsächlichen Strahlungsstärke darstellt.
Rechenschieber
Bevor elektronische Rechenmaschinen zur Verfügung standen, nutzte man die Logarithmengesetze aus, um Multiplikationen zu Additionen und Divisionen zu Subtraktionen zu vereinfachen. Die Berechnung der Quadratwurzel vereinfacht sich auf der Ebene des Logarithmus zu einer Division durch Zwei. Weil der Logarithmus selbst nicht so leicht zu berechnen ist, waren Rechenschieber mit ihren logarithmischen Skaleneinteilungen und Logarithmentafeln weit verbreitete Hilfsmittel.
Wachstums- und Zerfallsprozesse
Typische Aufgabenstellungen bei Wachstums- und Zerfallsprozessen lassen sich durch die Umkehrfunktion des Logarithmus – die Exponentialfunktion – modellieren. Siehe Exponentieller Vorgang, Absorption.
Anzahl der Ziffern einer Zahl
Berechnung der Anzahl der Ziffern, die zur Darstellung einer natürlichen Zahl
in einem Stellenwertsystem
benötigt werden. Um eine natürliche Zahl
zur Basis
darzustellen, werden
Stellen benötigt. Die Klammern
bedeuten dabei Abrunden auf die nächste ganze Zahl, die kleiner oder gleich ist.
Zum Beispiel ist .
Die obige Formel liefert den Wert 7. Man braucht also 7 Ziffern, um
100 im Dualsystem darzustellen,
nämlich
.
Stellt man hingegen 100 im Hexadezimalsystem
dar, dann benötigt man dazu zwei Stellen, denn
.
Es ist
.
Benfordsches Gesetz
Die Verteilung der Ziffern von Zahlen in empirischen Datensätzen, zum Beispiel ihrer ersten Ziffern, folgt einer logarithmischen Verteilung, dem Benfordschen Gesetz.
Informationseinheit
Messung der Informationsmenge;
die Informationstheorie
sagt, dass, wenn etwas mit Wahrscheinlichkeit
auftritt, das Wissen über das tatsächliche Auftreten davon eine
Informationsmenge von
bit ergibt. Zum Beispiel erhält man beim Ergebnis „Kopf“ eines fairen Münzwurfs (
)
die Informationsmenge
bit, und es genügt ein Bit, um diese Information zu codieren.
Kryptographie
Der diskrete Logarithmus ist in endlichen Körpern und darauf definierten elliptischen Kurven erheblich aufwändiger zu berechnen als seine Umkehrfunktion, die diskrete Exponentialfunktion. Letztere kann daher als sogenannte Einwegfunktion in der Kryptografie zur Verschlüsselung angewandt werden.
Logarithmische Zeitskalen
Logarithmische Zeitskalen finden sich in der Geschichte der Technik ebenso wie in der geologischen Zeitskala.
Intervalle der Musiktheorie
Intervalle haben einen exponentiellen Frequenzverlauf. Das Gehör jedoch empfindet diese als linear. Die Größenverhältnisse werden daher als Logarithmen angegeben. Die Oktave wird dabei in 1200 Cent (Musik) unterteilt. Beispiel:
-
Intervall Frequenzverhältnis Größe 1 Oktave 2 1200 Cent 2 Oktaven 4 2400 Cent 3 Oktaven 8 3600 Cent … große Terz 5:4 Quinte 3:2
Graphische Darstellung von Funktionen
Zur graphischen Darstellung von Funktionen werden spezielle mathematische Papiere verwendet, wie beispielsweise einfachlogarithmisches Papier oder doppeltlogarithmisches Papier.
Bezeichnungen
Man schreibt für den Logarithmus von
zur Basis
und sagt: „
ist der Logarithmus von
zur Basis
“.
heißt Numerus oder veraltet auch Logarithmand.
Das Ergebnis
des Logarithmierens gibt also an, mit welchem Exponenten man die Basis
potenzieren muss, um den Numerus
zu erhalten.
Für die Vorkommastellen des Logarithmus wird meist der Begriff Charakteristik (manchmal auch Kennzahl) verwendet, seine Nachkommastellen werden Mantisse genannt.

Das allgemeine mathematische Zeichen für den Logarithmus gemäß DIN 1302. Seltener findet man
auch davon abweichende Schreibweisen, wie zum Beispiel .
Das Zeichen
ohne eine angegebene Basis wird verwendet, wenn die verwendete Basis keine Rolle
spielt, wenn diese getrennt vereinbart wird, aus dem Zusammenhang ersichtlich
ist oder aufgrund einer Konvention festgelegt ist. In technischen Anwendungen
(so z.B. auf den meisten Taschenrechnern) steht
oft für den dekadischen Logarithmus. In theoretischen Abhandlungen,
insbesondere zu zahlentheoretischen
Themen, steht
oft für den natürlichen Logarithmus.
Darüber hinaus sind für den Logarithmus in DIN 1302 je nach Anwendung spezielle Schreibweisen festgelegt:
Natürlicher
Logarithmus (lateinisch
logarithmus
naturalis), der Logarithmus zur Basis ,
der Eulerschen
Zahl 2,7182818… Er wird im Zusammenhang mit Exponentialfunktionen
verwendet.
Dekadischer Logarithmus, auch als Zehnerlogarithmus oder Briggsscher Logarithmus bezeichnet, der Logarithmus zur Basis 10. Er wird bei numerischen Rechnungen im Dezimalsystem verwendet.
Binärer Logarithmus, auch als Zweierlogarithmus bezeichnet, der
Logarithmus zur Basis 2. Er wird in der Informatik bei Rechnungen im Binärsystem verwendet.
Außerhalb der Norm wird mit gleicher Bedeutung auch
– logarithmus dualis – verwendet.
Ein ähnlich aussehendes Funktionszeichen ist
für den Integrallogarithmus.
Bei dieser Funktion handelt es sich aber nicht um eine
Logarithmusfunktion.
Definition
Der Logarithmus kann mathematisch stets als eine Schar von Funktionen (deren
Parameter mit
bezeichnet sei) von
aufgefasst werden. Ihre einzelnen Logarithmusfunktionen sind dabei nur
unterschiedliche (reelle, aber ungleich null) Vielfache voneinander.
Über den positiven reellen Zahlen kann er auf verschiedene Arten eingeführt
werden. Je nach Hintergrund und Intention wird man den einen oder anderen
didaktischen Zugang wählen. Die verschiedenen Definitionen des reellen
Logarithmus sind dabei untereinander äquivalent
und erfolgen hier mit besonderem Fokus auf den natürlichen Logarithmus, der aus
Sicht des Mathematikers auf natürliche Weise auftritt, wie bei dem Zugang
über die Stammfunktion
von
erkennbar ist.
Als Umkehrfunktion der Exponentialfunktion
Der Logarithmus zur Basis
ist die Umkehrfunktion der allgemeinen Exponentialfunktion
zur positiven Basis
:
Die Funktionen
und
sind also Umkehrfunktionen
voneinander, d.h. Logarithmieren macht Exponenzieren rückgängig und
umgekehrt:
Der natürliche Logarithmus ergibt sich mit der Basis ,
wobei
die Eulersche Zahl ist.
Als Lösung einer Funktionalgleichung
Die Logarithmusfunktionen sind die nicht-trivialen, stetigen Lösungen
der Funktionalgleichung
Ihre Lösungen erfüllen stets
und erweisen sich sogar als differenzierbar. Den natürlichen Logarithmus erhält
man dann zusammen mit der Zusatzbedingung
Die Zusatzbedingung ist einer der Gründe dafür, den so erhaltenen Logarithmus
als natürlich zu bezeichnen. Wollte man den Logarithmus zu einer anderen
Basis
über die Zusatzbedingung erhalten, dann müsste man
fordern und würde wieder den natürlichen Logarithmus benötigen.
Die triviale Lösung obiger Funktionalgleichung ist die Nullfunktion ,
die nicht als Logarithmusfunktion angesehen wird, und die einzige Lösung der
Funktionalgleichung, für die auch
definiert ist.
Der Logarithmus vermittelt aufgrund obiger Funktionalgleichung daher insbesondere eine strukturerhaltende Abbildung von den positiven reellen Zahlen mit ihrer multiplikativen Struktur auf die gesamten reellen Zahlen mit deren additiver Struktur. Dies kann man auch explizit als Bedingung fordern und gelangt damit zur Herleitung.
Als Isomorphismus
Die reellwertigen Logarithmen sind genau die stetigen Isomorphismen
.
Diese Definition legt die Funktion
bis auf eine multiplikative Konstante eindeutig fest.
Der algebraische Zugang betont ebenso wie der Zugang über die Funktionalgleichung die historische Bedeutung des Logarithmus als Rechenhilfe: Er ermöglicht es, eine Multiplikation in eine Addition „umzuwandeln“.
Als Stammfunktion von f mit f(x)=1/x
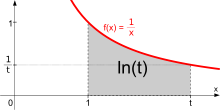
Die Funktion
mit
ist gerade der natürliche Logarithmus: Es ist
.
Zum Logarithmus mit der Basis
gelangt man durch Division der Funktion
durch die Konstante
.
Als uneigentliches Integral von
,
oder beliebiger willkürlicher (positiver) unterer Integrationsgrenze,
betrachtet, würde man nur noch eine zusätzliche, additive Konstante erhalten,
aber immer nur den Logarithmus zur Basis
bekommen.
Als Potenzreihe
Der natürliche Logarithmus kann als Potenzreihe gemäß
eingeführt werden. Diese Reihe konvergiert für
und für
.
Für eine numerische Berechnung des Werts
für
ist die Beziehung
nützlich.
Anmerkung
Diese Definitionen können auch herangezogen werden, um Logarithmen auf anderen mathematischen Strukturen zu erhalten, wie z.B. auf den komplexen Zahlen. Das setzt voraus, dass in der betreffenden Struktur die zur Definition verwendeten Konzepte existieren.
Um etwa den diskreten Logarithmus auf einer Gruppe zu definieren, können Konzepte wie Differentiation/Integration nicht herangezogen werden, weil sie dort gar nicht existieren. (Die Definition geschieht dort als Umkehrung der Potenzierung mit ganzen Exponenten, die wiederum aus mehrfachem Anwenden der einen Verknüpfung der Gruppe definiert ist.)
Rechenregeln und grundlegende Eigenschaften
Logarithmengesetze
Im Folgenden wird stets vorausgesetzt, dass die Variablen
von Null verschieden sind; im Falle des reellen Logarithmus werden die Zahlen
sogar als positiv vorausgesetzt. Die Basen
des Logarithmus dürfen ferner nicht 1 sein.
Produkte
Für das Rechnen mit Logarithmen von Produkten steht die hilfreiche Rechenregel
zur Verfügung; oder allgemeiner:
bzw.
Der Logarithmus eines Produkts ist die Summe der Logarithmen der Faktoren.
Quotienten
Die Quotienten leiten sich direkt aus den Logarithmen von Produkten ab. Hier sei nur der einfache Fall
angegeben. Der Logarithmus eines Quotienten ist der Logarithmus des Zählers
minus den Logarithmus des Nenners
.
Insbesondere ergibt sich daraus (da ):
Allgemeiner ergibt sich direkt aus der obigen Quotientenregel das Reziprozitätsgesetz:
Summen und Differenzen
Aus der Formel für Produkte kann eine Formel für Logarithmen von Summen (und
Differenzen) wie
hergeleitet werden, indem
ausgeklammert wird:
Damit ergibt sich die „Regel“
Potenzen
Für Potenzen mit reellem Exponent
gilt die Regel
Der Logarithmus einer Potenz ist also das Produkt aus dem Exponenten mit dem Logarithmus der Basis.
Auch daraus lässt sich für
ermitteln.
Der Logarithmus eines Stammbruchs
ist der negative Logarithmus des Nenners
.
Diese Rechenregeln lassen sich von den Potenzgesetzen ableiten.
Wurzeln
Da Wurzeln nichts anderes als Potenzen mit gebrochenem Exponenten sind, ergibt sich nach der oben angegebenen Potenzregel des Logarithmus die Rechenregel
Basisumrechnung
Um Logarithmen zur Basis
mithilfe von Logarithmen einer beliebigen Basis
zu berechnen, verwendet man den Zusammenhang
denn mit
gelten die Umformungen
Damit sieht man, dass sich Logarithmen zu verschiedenen Basen nur um einen konstanten Faktor voneinander unterscheiden. Die meisten Tabellenwerke stellen Logarithmen nur zur Basis 10 zur Verfügung, Taschenrechner auch zur Basis e (den natürlichen Logarithmus). Mit obiger Formel lassen sich daraus Logarithmen zu einer beliebigen Basis berechnen.
Ein prominenter Spezialfall, der sich aus obiger Formel ergibt, lautet:
oder
- Beispiel
- für beliebige positive Zahlen
ist
Nichtpositive Zahlen
In den reellen
Zahlen ist der Logarithmus für nichtpositive Zahlen, also Null und negative Zahlen, nicht
definiert. Allerdings erfüllt
obige Funktionalgleichung für
,
solange nur
ist, da diese dort eine Unstetigkeitsstelle hat. Ansonsten würde für
ja für alle
stets
folgen, wenn man ihre Gültigkeit auf ganz
,
also auch bei
,
verlangen würde.
müsste dann
bedeuten. Ist
ungleich Null, ist dies jedoch für kein reelles
lösbar.
- (als Beispiel die negative Zahl −1)
müsste dann
bedeuten. Dies ist ebenfalls für keine reelle Zahl
möglich, wenn
größer Null ist.
In der Funktionentheorie, in der Funktionen von komplexen Zahlen betrachtet werden, kann man den Logarithmus auch für negative Zahlen definieren (siehe Komplexer Logarithmus), allerdings gelten dann einige der Rechenregeln nicht mehr. Auch in diesem Zusammenhang ist 0 keine isolierte Singularität, sondern ein Verzweigungspunkt.
Ableitung und Integral
Die natürliche Logarithmusfunktion ist die Umkehrfunktion der Exponentialfunktion. Daher erhält man die Ableitung des natürlichen Logarithmus einfach durch Anwendung der Umkehrregel (siehe Beispiel dort). Es ergibt sich
für positives .
Für negatives
folgt daraus (wegen
und unter Anwendung der Kettenregel)
und wegen
lässt sich beides zu
zusammenfassen. Für allgemeine Logarithmen gilt:
Für alle reellen
ist
wobei für positives
(wenn also über den Pol bei
integriert wird) der Hauptwert
des Integrals zu nehmen ist.
Die Stammfunktion (auch bekannt als unbestimmtes Integral) des natürlichen Logarithmus lässt sich durch partielle Integration gewinnen:
Ist bei einem bestimmten Integral des natürlichen Logarithmus eine der Grenzen Null, so kann die Regel von de l’Hospital angewendet werden.
- Beispiel
da
Kurvendiskussion
- Definitionsmenge:
- Wertemenge:
- Nullstellenmenge bzw. Kurvenschnittpunkte mit den Koordinatenachsen: {1} bzw. (1|0)
- Asymptotisches Verhalten:
- Erste Ableitung:
- Extrempunkte: keine
- Wendepunkte: keine
- Monotonie:
streng monoton steigend/wachsend (wenn
) bzw. fallend (wenn
)
- Flächeninhalt
der Fläche zwischen Kurve, y-Achse und x-Achse bis x ≤ 1:
- Krümmungsextremum bei
mit
Natürlicher Logarithmus
Der Logarithmus zur Basis
(der Eulerschen
Zahl) wird auch als natürlicher Logarithmus bezeichnet und mit „ln“
oder oft auch „log“ (ohne Tiefstellung)
abgekürzt:
- Wenn
, dann ist
- – oder einfacher formuliert:
Die Zahl
ist z.B. dadurch ausgezeichnet (und könnte auch so definiert werden), dass
die Exponentialfunktion
sich bei Ableitung nach
wieder selbst reproduziert, als Formel:
Der Begriff natürlicher Logarithmus wurde gewählt, weil sowohl die
Exponentialfunktion als auch der Logarithmus zur Basis
in vielen Zusammenhängen (Integralrechnung,
Differentialrechnung,
Komplexe
Zahlen, Trigonometrie)
auf natürliche Weise ohne Vorfaktoren auftreten. Insbesondere lässt sich der
natürliche Logarithmus sehr einfach integrieren und differenzieren.
Der natürliche Logarithmus
ist eine Stammfunktion
der Kehrwertfunktion
mit
,
nämlich genau die mit
.
Berechnung des Logarithmus
Die Berechnung eines Logarithmus ist prinzipiell kompliziert. Sie lässt sich „mit Papier und Bleistift“ nur durch die vielfache Wiederholung bestimmter Rechenvorgänge erreichen, wobei das Ergebnis des gerade ausgeführten Schrittes als Ausgangsbasis für den nächsten Rechenschritt verwendet wird (Iterative Vorgehensweise). Meist kann man sich dem Wert nur annähern (Approximation). Dazu gibt es verschiedene mögliche Vorgehensweisen, von denen einige im Folgenden dargestellt sind. Anfangs ist das Ergebnis dieser Teilschritte jeweils relativ weit entfernt von dem korrekten Ergebnis, wird aber bei jedem weiteren Rechenschritt genauer, es konvergiert zu dem korrekten Ergebnis. Solche iterativen Rechenoperationen sind sehr gut geeignet, um sie automatisch mit einem Taschenrechner oder Computer auszuführen, wo lediglich eine Taste gedrückt werden muss (falls auf dem Gerät vorgesehen), um den Logarithmus der eingegebenen Zahl zu einer festgelegten Basis (meist die Eulersche Zahl e (2,718…) oder die Zahl 10) zu berechnen. Die folgenden Rechenbeispiele sind jeweils nur zur Berechnung des Logarithmus einer beliebigen Zahl zur Basis e (natürlicher Logarithmus) oder 2 geeignet.
Potenzreihe
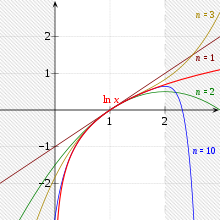
Die Potenzreihenentwicklung des natürlichen Logarithmus um den
Entwicklungspunkt 1 ergibt sich für
als
Sie konvergiert nicht sonderlich schnell an den Rändern des
Konvergenzintervalls, das Restglied der -ten
Partialsumme hat die Größe
Diese Reihe lässt sich auch als Kettenbruch darstellen:
Mit Hilfe der Formel
kann man die Berechnung des Logarithmus für beliebige
auf die für Werte im Interval
reduzieren, d.h., man findet immer
und
mit
und
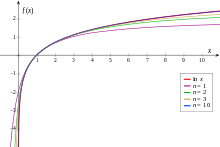
Mehr Flexibilität in der Reduktion auf Zahlen nahe 1 und eine Halbierung des
Berechnungsaufwandes bietet folgende Reihendarstellung,
die auf der Potenzreihenentwicklung des Areatangens
hyperbolicus
beruht,
mit der Restgliedabschätzung
Die Reihe konvergiert für ,
zeigt für
und
ähnliches Konvergenzverhalten und konvergiert umso besser, je näher
bei 1 liegt. Um dies zu erreichen, verwendet man wieder
Durch Wahl einer geeigneten ganzen Zahl
kann man immer erreichen, dass gilt
und erhöht damit die Konvergenzgeschwindigkeit der Reihe, die man jetzt für
berechnet. Allerdings muss man zusätzlich noch eine Näherung für
berechnen, was über die gleiche Reihe erfolgt. Eine solche Transformation auf
ein Intervall
durch Skalierung von
mit
ist auch für andere Werte von
möglich, durch die besonders einfache Handhabung der 2 in binär
dargestellten Zahlen wird selten ein anderer Faktor verwendet.
Additive Zerlegung
Der natürliche Logarithmus
steht, wie im obigen Abschnitt erwähnt, mit dem Areatangens
hyperbolicus
per
in Beziehung, was nach der anderen Seite aufgelöst
ergibt.
Die Logarithmen der positiv-ganzzahligen Numeri lassen sich damit in aufsteigenden Einerstufen der Form
darstellen und ausrechnen. Dabei verbessert sich das Konvergenzverhalten der Taylorreihe
geringfügig mit wachsendem
Mithilfe des Additionstheorems
lässt sich
und damit auch
additiv zerlegen. So ergeben sich beispielsweise die folgenden Identitäten für
die natürlichen Logarithmen der ersten Primzahlen. Dabei werde der
Übersichtlichkeit halber das Additionstheorem als Gruppengesetz
[1]
sowie seine -fache
Vervielfältigung als
formuliert.
-
sowie
Für die praktische Rechnung sind Zerlegungen bevorzugt, deren Summanden eine Eins im Zähler haben. Wie beim Arkustangens bleiben bei der Verdoppelung
die Einsen im Zähler erhalten.
Grenzwerte nach Hurwitz
Für den natürlichen Logarithmus gelten die Grenzwerte
sowie gleichbedeutend damit
die man leicht mit der Regel von de l’Hospital bestätigt.
Hierauf basieren die von Adolf
Hurwitz für den natürlichen Logarithmus angegebenen Grenzwerte der Folgen
bzw.
,
die über
wobei
definiert sind. Wegen
und weil
monoton fallend und
monoton wachsend ist, folgt die Konvergenz dieser beiden Folgen. Aufgrund von
und
ergibt sich die Gleichheit der beiden Grenzwerte:
Für eine praktische Berechnung von ln
sind diese Grenzwerte wegen der auftretenden Auslöschung
jedoch nicht gut geeignet.
Berechnung einzelner Binärziffern
Eine weitere Möglichkeit zur Berechnung des Logarithmus besteht darin, nacheinander die Ziffern der Binärdarstellung des Logarithmus zur Basis 2 zu bestimmen. Dieses Verfahren ist besonders einfach auf Rechenwerken zu implementieren, da es aufwändige Divisionen vermeidet und auch leicht in Festkomma-Arithmetik umsetzbar ist.
Zunächst werden die Vorkommastellen des Zweierlogarithmus (immer im Dualsystem) durch Abzählen
der Vorkommastellen der Zahl
bestimmt und
durch Schieben
auf Werte zwischen 1 und 2 normiert.
Der Logarithmus von
hat danach die Darstellung
Quadrieren von
schiebt den Logarithmus also um eine Binärstelle nach links, wodurch die
Vorkommastelle möglicherweise Eins wird. Dies ist dann der Fall, wenn
ist. In diesem Falle wird
durch Division durch 2 wieder normiert, was keinen Einfluss auf die
verbleibenden Nachkommastellen hat. Damit ergibt sich die folgende Skizze des
Verfahrens:
INPUT 1 ≤ x < 2 OUTPUT Nachkommastellen bi der Binärdarstellung von log2(x)
i ← 0
LOOP
i ← i + 1
x ← x2
IF x ≥ 2 THEN
x ← x / 2
bi ← 1
ELSE
bi ← 0
END IF
END LOOP
Analogrechner
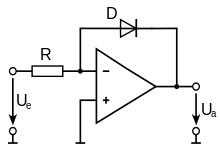
Zur Berechnung des Logarithmus mithilfe eines Analogrechners
– also etwa der Erzeugung einer elektrischen Ausgangsspannung
,
die den Logarithmus des Nennwerts der Eingangsspannung
annimmt – kann man sich den exponentiellen Verlauf der
Strom-Spannungs-Kennlinie
einer Diode
zunutze machen. Die nebenstehende Skizze zeigt den prinzipiellen Aufbau eines
Logarithmierers mit einem Operationsverstärker,
einer Diode
und einem Widerstand
.
Komplexer Logarithmus
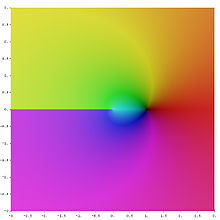
Analog zur reellen Definition heißt jede komplexe Zahl ,
welche die Gleichung
erfüllt, ein natürlicher Logarithmus von .
Für jedes
existiert ein solches
,
das jedoch im Unterschied zum reellen Logarithmus wegen
,
nicht eindeutig bestimmt ist. Hat man also einen Logarithmus
von
gefunden, so ist damit auch
mit jeder ganzen Zahl
ein Logarithmus von
,
denn es gilt
.
Um Eindeutigkeit zu erreichen, wählt man aus den möglichen Werten für
solche Werte aus, die in einem geeigneten Streifen der komplexen Zahlenebene
liegen. Man kann z.B. den Streifen
verwenden. Ein Wert
aus diesem Streifen heißt Hauptwert (englisch principal value) des
Logarithmus, und man schreibt
.
Stellt man
in Polarform
dar, so erhält man eine einfache Darstellung des k-ten Zweiges der
Logarithmusfunktion:
mit der Argument-Funktion
.
Im Summanden
wird der bereits oben definierte reelle Logarithmus
verwendet. Für
erhält man den Hauptzweig des komplexen Logarithmus zurück:
.
ist nicht stetig auf
.
Entfernt man jedoch die negative reelle Achse, so ist
auf dem Gebiet
stetig und sogar holomorph.
- Zur Beachtung
Für den Hauptzweig des komplexen Logarithmus
gelten nicht alle der weiter oben angeführten Rechenregeln
für die reelle Logarithmusfunktion. Sie gelten nur
. Diese Mehrdeutigkeit ist eine direkte Folge aus der Periodizität seiner
Umkehrfunktion, der komplexen Exponentialfunktion. Der Vergleich von
mit
zeigt, dass
nicht für alle von
verschiedenen komplexen Zahlen
und
richtig ist. Auch die Gleichung
ist nicht immer erfüllt, wie das Gegenbeispiel
beweist.
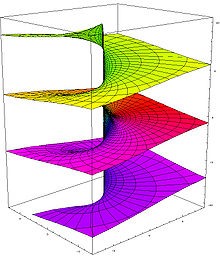
- Grafische Darstellung des komplexen Logarithmus
-
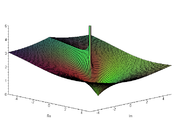 Betrag von
Betrag von -
 Realteil von
Realteil von -
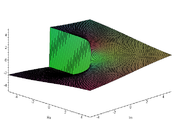 Imaginärteil von
Imaginärteil von
Mit dem oben definierten Hauptzweig des komplexen Logarithmus kann man den Logarithmus von negativen reellen Zahlen erklären:
Das setzt voraus, dass die Argument-Funktion
negativen reellen Zahlen den Wert
zuweist.
Diese Betrachtungen zeigen, dass die Mehrdeutigkeit des komplexen Logarithmus letztlich auf die Mehrdeutigkeit der Argument-Funktion zurückzuführen ist.
Diskrete Logarithmen
Diskrete Logarithmen sind Lösungen von Gleichungen der Form
über einer endlichen zyklischen
Gruppe .
Der diskrete Logarithmus
von
zur Basis
ist modulo
der Gruppenordnung
von
eindeutig bestimmt und existiert – da
ein Erzeuger der Gruppe ist – für alle Elemente der Gruppe.
Diskrete Logarithmen sind im Sinne der Komplexitätstheorie für viele Gruppen aufwändig zu berechnen und finden Anwendung in der Kryptographie, etwa in auf elliptischen Kurven basierenden Kryptosystemen.
Beispiel:
hat als Lösung den Wert 4, denn es gilt 24 = 16, und 16 lässt
den Rest 5 bei Division
mit Rest durch 11. Die Lösung ist eindeutig modulo 10, also modulo der
Gruppenordnung von .
Dementsprechend ist mit
auch
eine Lösung der Kongruenz.
Siehe auch
- Exponentialfunktion
- Eulersche Zahl
- Logarithmische Spirale
- Matrixlogarithmus
- Verallgemeinerter Logarithmus
Literatur
- Eric
W. Weisstein:
 Logarithm. In: MathWorld
(englisch).
Logarithm. In: MathWorld
(englisch). - Wolfgang Walter: Analysis I. Grundwissen Mathematik Band 3. Springer, Berlin 1985, ISBN 3-540-12780-1.
- Klaus Jänich: Funktionentheorie. Eine Einführung. Springer, Berlin 2004, ISBN 3-540-20392-3.
- I. N. Bronstein, K. A. Semendjajew, G. Musiol, H. Mühlig (Hrsg.): Taschenbuch der Mathematik. 10., überarbeitete Auflage. Europa-Lehrmittel, Haan-Gruiten 2016, ISBN 978-3-8085-5790-7.
- Ernst Hairer, Gerhard Wanner: Analysis in historischer Entwicklung. Springer-Verlag, Berlin / Heidelberg 2011, ISBN 978-3-642-13766-2.
Anmerkungen
- ↑
Da
und
Umkehrfunktionen voneinander sind, sind die Gruppenaxiome leicht nachgerechnet. Das Inverse
von
ist wegen der Ungeradheit dieser Funktionen


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 20.01. 2024