
Nullfunktion
Die Nullfunktion ist in der Mathematik, insbesondere der Analysis, eine Funktion, deren Funktionswert unabhängig vom übergebenen Wert immer die Zahl Null ist. Allgemeiner ist die Nullabbildung oder der Nulloperator in der linearen Algebra eine Abbildung zwischen zwei Vektorräumen, die stets den Nullvektor des Zielraums ergibt. Noch allgemeiner wird die Nullabbildung in der Algebra gefasst und dort ist sie eine Abbildung von einer beliebigen Menge in eine Menge, auf der eine Verknüpfung mit neutralem Element definiert ist, die immer dieses neutrale Element ergibt. Die Nullfunktion hat viele Eigenschaften und wird in der Mathematik oft als Beispiel oder als Gegenbeispiel verwendet. Sie ist die triviale Lösung einer Reihe mathematischer Probleme, wie zum Beispiel homogener linearer Differentialgleichungen und Integralgleichungen.
Reelle Nullfunktion
Definition
In der reellen Analysis
ist die Nullfunktion die reelle Funktion
,
die jedem Argument die Zahl Null
zuordnet, das heißt, es gilt
für alle .
Mit Hilfe des Identitätssymbols
wird die Nullfunktion auch durch
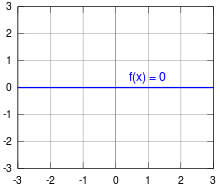
notiert. Der Graph
der Nullfunktion ist die gesamte x-Achse.
Gelegentlich wird der Definitionsbereich
der Nullfunktion auch auf eine Teilmenge
eingeschränkt.
Eigenschaften
Einordnung
Die Nullfunktion ist ein Spezialfall folgender Funktionenklassen:
- Sie ist eine spezielle konstante
Funktion
, und zwar gerade diejenige, deren Konstante
ist.
- Sie ist eine spezielle lineare
Funktion
, und zwar diejenige, deren Steigung
und Ordinatenabschnitt
sind.
- Sie ist eine spezielle Polynomfunktion
, nämlich das Nullpolynom, bei dem alle Koeffizienten
sind. Der Grad des Nullpolynoms wird meist nicht als
, sondern als
definiert.
Symmetrien
Die Nullfunktion ist als einzige Funktion gleichzeitig gerade und ungerade, das heißt, es gilt
.
Weiter ist sie weder positiv noch negativ, stattdessen ist sie sowohl nichtpositiv als auch nichtnegativ, also
und
.
Die Nullstellen der Nullfunktion sind damit alle Zahlen der Definitionsmenge und ihre Nichtnullstellenmenge ist demnach leer. Das Minimum und das Maximum der Nullfunktion sind ebenfalls Null:
.
Weiterhin ist die Nullfunktion, wie jede konstante Funktion, gleichzeitig monoton steigend und fallend (jedoch nicht streng) und, wie jede lineare Funktion, gleichzeitig konvex und konkav.
Ableitungen
Die Nullfunktion ist eine glatte Funktion, also beliebig oft stetig differenzierbar, wobei jede ihrer Ableitungen wieder die Nullfunktion selbst ist, das heißt
für jedes .
Neben der Exponentialfunktion
ist die Nullfunktion die einzige Funktion mit dieser Eigenschaft. Die
Nullfunktion selbst ist wiederum die Ableitung einer konstanten Funktion und
allgemein die
-te
Ableitung eines Polynoms vom Grad
.
Integral
Das Integral der Nullfunktion ergibt unabhängig von den Integrationsgrenzen immer Null, also
.
für alle .
Die Nullfunktion ist damit die einzige Polynomfunktion, die über den gesamten
reellen Zahlen integrierbar ist. Stammfunktion
der Nullfunktion ist die Nullfunktion selbst und, da die Integrationskonstante
frei wählbar ist, auch jede konstante Funktion.
Lösung von Gleichungen
Die Nullfunktion ist die triviale Lösung der vier Cauchy-Funktionalgleichungen:
Weiter löst die Nullfunktion jede homogene lineare Differentialgleichung der Form
und jede homogene lineare Integralgleichung der Art
mit Integralkern
und Vorfaktor
.
Umgekehrt wird eine inhomogene lineare Differential- oder Integralgleichung nie
durch die Nullfunktion gelöst.
Nullabbildungen zwischen Vektorräumen
Definition
In der linearen
Algebra heißt eine Abbildung
zwischen zwei Vektorräumen
und
über dem gleichen Körper
Nullabbildung oder Nulloperator, wenn für alle Vektoren
gilt, wobei
der eindeutig bestimmte Nullvektor
von
ist. Gelegentlich wird die Nullabbildung auch direkt durch
notiert, sofern aus dem Kontext klar ist, ob die Nullabbildung oder die Zahl
Null gemeint ist. Auch hier kann der Definitionsbereich der Nullabbildung auf
eine Teilmenge
eingeschränkt werden.
Beispiele
- die reelle Nullfunktion des vorangegangenen Abschnitts und allgemeiner reelle oder komplexe Funktionen ein oder mehrerer Variablen, deren Funktionswert die Zahl Null oder der Nullvektor ist
- jede Abbildung von einem beliebigen Vektorraum
in den Nullvektorraum
und jede lineare Abbildung vom Nullvektorraum in einen beliebigen Vektorraum
- eine quadratische Matrix, die in ihr charakteristisches Polynom eingesetzt wird, nach dem Satz von Cayley-Hamilton
- die Determinantenfunktion auf der Menge der singulären quadratischen Matrizen
Eigenschaften
Linearität
Die Nullabbildung ist eine lineare Abbildung, also ein Vektorraumhomomorphismus, das heißt, es gilt
für alle
und
.
Sie liegt also im Vektorraum
der linearen Abbildungen
und ist dort selbst der Nullvektor.
Jede Nullabbildung zwischen endlichdimensionalen Vektorräumen wird bezüglich
beliebiger Basen durch eine Nullmatrix
der Größe
dargestellt.
Ihr Kern
ist ganz
,
ihr Bild
und somit ihr Rang
immer
.
Ist
,
dann ist besitzt die Nullabbildung als einzigen Eigenwert die Zahl Null und
der zugehörige Eigenraum ist ganz
.
Operatornorm
Sind
und
normierte Räume mit
jeweiligen Normen
und
,
dann ist die Operatornorm
der Nullabbildung
.
Die Nullabbildung selbst stellt für
eine Halbnorm dar.
Lösung von Gleichungen
Allgemein löst die Nullabbildung jede homogene lineare Operatorgleichung
,
wobei
ein linearer
Operator ist,
die gesuchte Funktion und
die Nullfunktion ist. Umgekehrt wird eine inhomogene lineare Operatorgleichung,
bei der also die rechte Seite ungleich der Nullfunktion ist, nie durch die
Nullabbildung gelöst.
Nullabbildungen in ein Magma mit Eins
Definition
Ist
eine Menge
und
ein Magma
mit Eins, das heißt eine Menge versehen mit einer zweistelligen Verknüpfung
mit neutralem
Element
,
dann heißt eine Abbildung
Nullabbildung, wenn für alle
gilt. Wichtige Beispiele für
sind Monoide,
Gruppen,
Ringe, Moduln und – wie im
vorangegangenen Abschnitt – Vektorräume.
Beispiele
- die boolesche Funktion der Kontradiktion in einen booleschen Ring bzw. eine boolesche Algebra
- die Polynomfunktion
in einem Polynomring über einem endlichen Körper mit
Elementen
- die
-te Potenz einer nilpotenten Abbildung in einen Ring, wenn
größer oder gleich dem Nilpotenzindex der Abbildung ist
- das Nullmaß,
das jeder Menge
den Wert
zuordnet
Eigenschaften
- Sind
und
zwei Magmen,
mit Eins, dann ist die Nullabbildung ein Magmenhomomorphismus.
- Sind
und
zwei Ringe, dann ist die Nullabbildung ein Ringhomomorphismus. Ist
ein einfacher Ring (beispielsweise ein Körper oder ein Schiefkörper), dann ist jeder Ringhomomorphismus entweder injektiv oder die Nullabbildung.
- Sind
und
zwei Moduln, dann ist die Nullabbildung ein Modulhomomorphismus.
- Sind
und
zwei Algebren über einem Ring, dann ist die Nullabbildung ein Algebrenhomomorphismus.
Siehe auch
Literatur
- Martin Barner, Friedrich Flohr: Analysis I. de Gruyter, 2000, ISBN 3-11-016778-6.
- Siegfried Bosch: Lineare Algebra. Springer, 2009, ISBN 3-540-76437-2.
- Christian Karpfinger, Kurt Meyberg: Algebra: Gruppen – Ringe – Körper. Springer, 2008, ISBN 3-8274-2018-0.
- Gilbert Strang: Lineare Algebra. Springer, 2003, ISBN 3-540-43949-8.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 24.09. 2022