
Matrix (Mathematik)
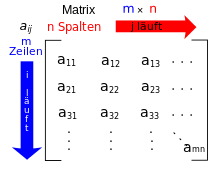
In der Mathematik versteht man unter einer Matrix (Plural Matrizen) eine rechteckige Anordnung (Tabelle) von Elementen (meist mathematischer Objekte, etwa Zahlen). Mit diesen Objekten lässt sich dann in bestimmter Weise rechnen, indem man Matrizen addiert oder miteinander multipliziert.
Matrizen sind ein Schlüsselkonzept der linearen Algebra und tauchen in fast allen Gebieten der Mathematik auf. Sie stellen Zusammenhänge, in denen Linearkombinationen eine Rolle spielen, übersichtlich dar und erleichtern damit Rechen- und Gedankenvorgänge. Sie werden insbesondere dazu benutzt, lineare Abbildungen darzustellen und lineare Gleichungssysteme zu beschreiben und zu lösen. Die Bezeichnung Matrix wurde 1850 von James Joseph Sylvester eingeführt.
Eine Anordnung, wie in nebenstehender Abbildung, von
Elementen
erfolgt in
Zeilen und
Spalten. Die Verallgemeinerung auf mehr als zwei Indizes wird
auch Hypermatrix genannt.
Begriffe und erste Eigenschaften
Notation
Als Notation hat sich die Anordnung der Elemente in Zeilen und Spalten zwischen zwei großen öffnenden und schließenden Klammern durchgesetzt. In der Regel verwendet man runde Klammern, es werden aber auch eckige verwendet. Zum Beispiel bezeichnen
und
Matrizen mit zwei Zeilen und drei Spalten. Matrizen werden üblicherweise mit
Großbuchstaben (manchmal fett gedruckt oder, handschriftlich, einfach oder
doppelt unterstrichen), vorzugsweise ,
bezeichnet. Eine Matrix mit
Zeilen und
Spalten:
.
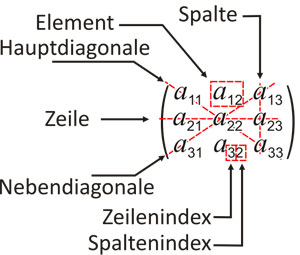
Elemente der Matrix
Die Elemente der Matrix nennt man auch Einträge oder
Komponenten der Matrix. Sie entstammen einer Menge
in der Regel einem Körper
oder einem Ring.
Man spricht von einer Matrix über
.
Wählt man für
die Menge der reellen
Zahlen, so spricht man von einer reellen Matrix, bei komplexen Zahlen von
einer komplexen Matrix.
Ein bestimmtes Element beschreibt man durch zwei Indizes, meist ist
das Element in der ersten Zeile und der ersten Spalte durch
beschrieben. Allgemein bezeichnet
das Element in der
-ten
Zeile und der
-ten
Spalte. Bei der Indizierung wird dabei stets als erstes der Zeilenindex und als
zweites der Spaltenindex des Elements genannt. Merkregel: Zeile zuerst,
Spalte später. Wenn Verwechslungsgefahr besteht, werden die beiden Indizes
mit einem Komma abgetrennt. So wird zum Beispiel das Matrixelement in der ersten
Zeile und der elften Spalte mit
bezeichnet.
Einzelne Zeilen und Spalten werden oft als Spalten- oder Zeilenvektoren bezeichnet. Ein Beispiel:
hier sind
und
die Spalten oder Spaltenvektoren sowie
und
die Zeilen oder Zeilenvektoren.
Bei einzeln stehenden Zeilen- und Spaltenvektoren einer Matrix wird gelegentlich der unveränderliche Index weggelassen. Manchmal werden Spaltenvektoren zur kompakteren Darstellung als transponierte Zeilenvektoren geschrieben, also:
oder
als
oder
Typ
Der Typ einer Matrix ergibt sich aus der Anzahl ihrer Zeilen und
Spalten. Eine Matrix mit
Zeilen und
Spalten nennt man eine
-Matrix
(sprich: m-mal-n- oder m-Kreuz-n-Matrix). Stimmen Zeilen- und
Spaltenanzahl überein, so spricht man von einer quadratischen Matrix.
Eine Matrix, die aus nur einer Spalte oder nur einer Zeile besteht, wird
üblicherweise als Vektor aufgefasst. Einen Vektor
mit
Elementen kann man je nach Kontext als einspaltige
-Matrix
oder einzeilige
-Matrix
darstellen. Neben den Begriffen Spaltenvektor und Zeilenvektor sind hierfür die
Begriffe Spaltenmatrix und Zeilenmatrix geläufig. Eine
-Matrix
ist sowohl Spalten- als auch Zeilenmatrix und wird als Skalar angesehen.
Formale Darstellung
Eine Matrix ist eine doppelt indizierte Familie. Formal ist dies eine Funktion
die jedem Indexpaar
als Funktionswert den Eintrag
zuordnet. Beispielsweise wird dem Indexpaar
als Funktionswert der Eintrag
zugeordnet. Der Funktionswert
ist also der Eintrag in der
-ten
Zeile und der
-ten
Spalte. Die Variablen
und
entsprechen der Anzahl der Zeilen bzw. Spalten. Nicht zu verwechseln mit dieser
formalen Definition einer Matrix als Funktion ist, dass Matrizen selbst lineare Abbildungen
beschreiben.
Die Menge
aller
-Matrizen
über der Menge
wird in üblicher mathematischer Notation auch
geschrieben; hierfür hat sich die Kurznotation
eingebürgert. Manchmal werden die Schreibweisen
oder seltener
benutzt.
Addition und Multiplikation
Auf dem Raum der Matrizen werden elementare Rechenoperationen definiert.
Matrizenaddition
Zwei Matrizen können addiert werden, wenn sie vom selben Typ sind, das heißt,
wenn sie dieselbe Anzahl von Zeilen und dieselbe Anzahl von Spalten besitzen.
Die Summe zweier -Matrizen
ist komponentenweise definiert:
Rechenbeispiel:
In der linearen Algebra sind die Einträge der Matrizen üblicherweise Elemente eines Körpers, wie der reellen oder komplexen Zahlen. In diesem Fall ist die Matrizenaddition assoziativ, kommutativ und besitzt mit der Nullmatrix ein neutrales Element. Im Allgemeinen besitzt die Matrizenaddition diese Eigenschaften jedoch nur, wenn die Einträge Elemente einer algebraischen Struktur sind, die diese Eigenschaften hat.
Skalarmultiplikation
Eine Matrix wird mit einem Skalar multipliziert, indem jeder Eintrag der Matrix mit dem Skalar multipliziert wird:
Rechenbeispiel:
Die Skalarmultiplikation darf nicht mit dem Skalarprodukt
verwechselt werden. Um die Skalarmultiplikation durchführen zu dürfen, müssen
der Skalar
(Lambda) und
die Einträge der Matrix demselben Ring
entstammen. Die Menge der
-Matrizen
ist in diesem Fall ein (Links-)Modul
über
Matrizenmultiplikation
Zwei Matrizen können multipliziert werden, wenn die Spaltenanzahl der linken
mit der Zeilenanzahl der rechten Matrix übereinstimmt. Das Produkt einer -Matrix
und einer
-Matrix
ist eine
-Matrix
deren Einträge berechnet werden, indem die Produktsummenformel, ähnlich dem
Skalarprodukt, auf Paare aus einem Zeilenvektor der ersten und einem
Spaltenvektor der zweiten Matrix angewandt wird:
Die Matrizenmultiplikation ist nicht kommutativ,
d.h., im Allgemeinen gilt .
Die Matrizenmultiplikation ist allerdings assoziativ,
d.h., es gilt stets:
Eine Kette von Matrix-Multiplikationen kann daher unterschiedlich geklammert werden. Das Problem, eine Klammerung zu finden, die zu einer Berechnung mit der minimalen Anzahl von elementaren arithmetischen Operationen führt, ist ein Optimierungsproblem. Die Matrizenaddition und Matrizenmultiplikation genügen zudem den beiden Distributivgesetzen:
für alle -Matrizen
und
-Matrizen
sowie
für alle -Matrizen
und
-Matrizen
Quadratische Matrizen
können mit sich selbst multipliziert werden, analog zur Potenz bei den reellen
Zahlen führt man abkürzend die Matrixpotenz
oder
ein. Damit ist es auch sinnvoll, quadratische Matrizen als Elemente in Polynome
einzusetzen. Zu weitergehenden Ausführungen hierzu siehe unter Charakteristisches
Polynom. Zur einfacheren Berechnung kann hier die jordansche
Normalform verwendet werden. Quadratische Matrizen über
oder
kann man darüber hinaus sogar in Potenzreihen einsetzen, vgl. Matrixexponential.
Eine besondere Rolle bezüglich der Matrizenmultiplikation spielen die
quadratischen Matrizen über einem Ring
,
also
.
Diese bilden selbst mit der Matrizenaddition und -multiplikation wiederum einen
Ring, der Matrizenring
genannt wird.
Weitere Rechenoperationen
Die transponierte Matrix
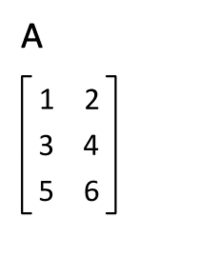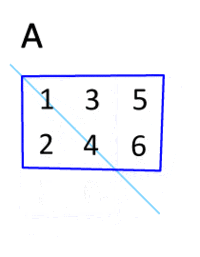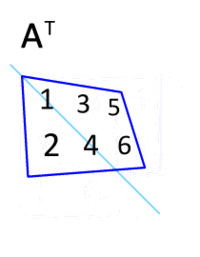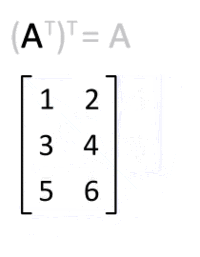
der Matrix A
Die Transponierte einer -Matrix
ist die
-Matrix
,
das heißt, zu
ist
die Transponierte. Man schreibt also die erste Zeile als erste Spalte, die
zweite Zeile als zweite Spalte usw. Die Matrix wird an ihrer Hauptdiagonalen
gespiegelt. Es gelten die folgenden Rechenregeln:
Bei Matrizen über
ist die adjungierte
Matrix genau die transponierte Matrix.
Inverse Matrix
Falls die Determinante
einer quadratischen -Matrix
über einem Körper
nicht gleich null ist, d.h., falls
,
so existiert die zur Matrix
inverse Matrix
.
Für diese gilt
,
wobei
die
-Einheitsmatrix ist.
Matrizen, die eine inverse Matrix besitzen, bezeichnet man als
invertierbare oder reguläre
Matrizen. Diese haben vollen Rang.
Umgekehrt werden nichtinvertierbare Matrizen als singuläre Matrizen
bezeichnet. Eine Verallgemeinerung der Inversen für singuläre Matrizen sind sog.
pseudoinverse Matrizen.
Vektor-Vektor-Produkte
Das Matrixprodukt
zweier
-Vektoren
und
ist nicht definiert, da die Anzahl
der Spalten von
im Allgemeinen ungleich der Anzahl
der Zeilen von
ist. Die beiden Produkte
und
existieren jedoch.
Das erste Produkt
ist eine
-Matrix,
die als Zahl interpretiert wird; sie wird das Standardskalarprodukt
von
und
genannt und mit
oder
bezeichnet. Geometrisch entspricht dieses Skalarprodukt in einem kartesischen
Koordinatensystem dem Produkt
der Beträge der beiden Vektoren und des Kosinus des von den beiden Vektoren eingeschlossenen Winkels. Beispielsweise gilt
Das zweite Produkt
ist eine
-Matrix
und heißt dyadisches
Produkt oder Tensorprodukt
von
und
(geschrieben
).
Seine Spalten sind skalare Vielfache von
,
seine Zeilen skalare Vielfache von
.
Beispielsweise gilt
Vektorräume von Matrizen
Die Menge der -Matrizen
über einem Körper
bildet mit der Matrizenaddition und der Skalarmultiplikation einen
-Vektorraum. Dieser
Vektorraum
hat die Dimension
.
Eine Basis von
ist gegeben durch die Menge der Standardmatrizen
mit
,
.
Diese Basis wird manchmal als Standardbasis
von
bezeichnet.
Die Spur
des Matrixprodukts
ist dann im Spezialfall
ein reelles Skalarprodukt.
In diesem euklidischen
Vektorraum stehen die symmetrischen
Matrizen und die schiefsymmetrischen
Matrizen senkrecht aufeinander. Ist
eine symmetrische und
eine schiefsymmetrische Matrix, so gilt
.
Im Spezialfall
ist die Spur des Matrixproduktes
ein komplexes Skalarprodukt und der Matrizenraum wird zu einem unitären Vektorraum. Dieses Skalarprodukt wird Frobenius-Skalarprodukt genannt. Die von dem Frobenius-Skalarprodukt induzierte Norm heißt Frobeniusnorm und mit ihr wird der Matrizenraum zu einem Banachraum.
Anwendungen
Zusammenhang mit linearen Abbildungen
Das Besondere an Matrizen über einem Ring
ist der Zusammenhang zu linearen
Abbildungen. Zu jeder Matrix
lässt sich eine lineare Abbildung mit Definitionsbereich
(Menge der Spaltenvektoren) und Wertebereich
definieren, indem man jeden Spaltenvektor
auf
abbildet. Umgekehrt entspricht jeder linearen Abbildung
auf diese Weise genau eine
-Matrix
;
dabei sind die Spalten von
die Bilder der Standard-Basisvektoren
von
unter
.
Diesen Zusammenhang zwischen linearen Abbildungen und Matrizen bezeichnet man
auch als (kanonischen) Isomorphismus
Er stellt bei vorgegebenem
und
eine Bijektion
zwischen der Menge der Matrizen und der Menge der linearen Abbildungen dar. Das
Matrixprodukt geht hierbei über in die Komposition (Hintereinanderausführung)
linearer Abbildungen. Weil die Klammerung bei der Hintereinanderausführung
dreier linearer Abbildungen keine Rolle spielt, gilt dies für die
Matrixmultiplikation, diese ist also assoziativ.
Ist
sogar ein Körper, kann man statt der Spaltenvektorräume beliebige
endlichdimensionale
-Vektorräume
und
(der Dimension
bzw.
)
betrachten. (Falls
ein kommutativer Ring mit 1 ist, dann kann man analog freie K-Moduln
betrachten.) Diese sind nach Wahl von Basen
von
und
von
zu den Koordinatenräumen
bzw.
isomorph, weil zu einem beliebigen Vektor
eine eindeutige Zerlegung in Basisvektoren
existiert und die darin vorkommenden Körperelemente
den Koordinatenvektor
bilden. Jedoch hängt der Koordinatenvektor von der verwendeten Basis
ab, die daher in der Bezeichnung
vorkommt.
Analog verhält es sich im Vektorraum
Ist eine lineare Abbildung
gegeben, so lassen sich die Bilder der Basisvektoren von
eindeutig in die Basisvektoren von
zerlegen in der Form
mit Koordinatenvektor
Die Abbildung ist dann vollständig festgelegt durch die sog. Abbildungsmatrix
denn für das Bild des o.g. Vektors
gilt
also
(„Koordinatenvektor = Matrix mal Koordinatenvektor“). (Die Matrix
hängt von den verwendeten Basen
und
ab; bei der Multiplikation wird die Basis
,
die links und rechts vom Malpunkt steht, „weggekürzt“, und die „außen“ stehende
Basis
bleibt übrig.)
Die Hintereinanderausführung zweier linearer Abbildungen
und
(mit Basen
,
bzw.
)
entspricht dabei der Matrixmultiplikation, also
(auch hier wird die Basis
„weggekürzt“).
Somit ist die Menge der linearen Abbildungen von
nach
wieder isomorph zu
Der Isomorphismus
hängt aber von den gewählten Basen
und
ab und ist daher nicht kanonisch: Bei Wahl einer anderen Basis
für
bzw.
für
wird derselben linearen Abbildung nämlich eine andere Matrix zugeordnet, die aus
der alten durch Multiplikation von rechts bzw. links mit einer nur von den
beteiligten Basen abhängigen invertierbaren
-
bzw.
-Matrix
(sog. Basiswechselmatrix)
entsteht. Das folgt durch zweimalige Anwendung der Multiplikationsregel aus dem
vorigen Absatz, nämlich
(„Matrix = Basiswechselmatrix mal Matrix mal Basiswechselmatrix“). Dabei
bilden die Identitätsabbildungen
und
jeden Vektor aus
bzw.
auf sich selbst ab.
Bleibt eine Eigenschaft von Matrizen unberührt von solchen Basiswechseln, so ist es sinnvoll, diese Eigenschaft basisunabhängig der entsprechenden linearen Abbildung zuzusprechen.
Im Zusammenhang mit Matrizen oft auftretende Begriffe sind der Rang und die Determinante
einer Matrix. Der Rang ist (falls
ein Körper ist) im angeführten Sinne basisunabhängig, und man kann somit vom
Rang auch bei linearen Abbildungen sprechen. Die Determinante ist nur für quadratische
Matrizen definiert, die dem Fall
entsprechen; sie bleibt unverändert, wenn derselbe Basiswechsel im Definitions-
und Wertebereich durchgeführt wird, wobei beide Basiswechselmatrizen zueinander
invers sind:
In diesem Sinne ist also die Determinante basisunabhängig.
Umformen von Matrizengleichungen
Speziell in den multivariaten Verfahren werden häufig Beweisführungen, Herleitungen usw. im Matrizenkalkül durchgeführt.
Gleichungen werden im Prinzip wie algebraische Gleichungen umgeformt, wobei jedoch die Nichtkommutativität der Matrixmultiplikation sowie die Existenz von Nullteilern beachtet werden muss.
Beispiel: Lineares Gleichungssystem als einfache Umformung
Gesucht ist der Lösungsvektor
eines linearen Gleichungssystems
mit
als
-Koeffizientenmatrix.
Wenn die inverse Matrix
existiert, kann man mit ihr von links multiplizieren:
und man erhält als Lösung
Spezielle Matrizen
Eigenschaften von Endomorphismen
Die folgenden Eigenschaften quadratischer Matrizen entsprechen Eigenschaften von Endomorphismen, die durch sie dargestellt werden.
- Orthogonale Matrizen
- Eine reelle Matrix
ist orthogonal, wenn die zugehörige lineare Abbildung das Standardskalarprodukt erhält, das heißt, wenn
- gilt. Diese Bedingung ist äquivalent dazu, dass
die Gleichung
- bzw.
- erfüllt.
- Diese Matrizen stellen Spiegelungen, Drehungen und Drehspiegelungen dar.
- Unitäre Matrizen
- Sie sind das komplexe Gegenstück zu den orthogonalen Matrizen. Eine
komplexe Matrix
ist unitär, wenn die zugehörige Transformation die Normierung erhält, das heißt, wenn
- gilt. Diese Bedingung ist äquivalent dazu, dass
die Gleichung
- erfüllt; dabei bezeichnet
die konjugiert-transponierte Matrix zu
- Fasst man den
-dimensionalen komplexen Vektorraum als
-dimensionalen reellen Vektorraum auf, so entsprechen die unitären Matrizen genau denjenigen orthogonalen Matrizen, die mit der Multiplikation mit
vertauschen.
- Projektionsmatrizen
- Eine Matrix ist eine Projektionsmatrix, falls
- gilt, sie also idempotent ist, das heißt, die mehrfache Anwendung einer Projektionsmatrix auf einen Vektor lässt das Resultat unverändert. Eine idempotente Matrix hat keinen vollen Rang, es sei denn, sie ist die Einheitsmatrix. Geometrisch entsprechen Projektionsmatrizen der Parallelprojektion entlang des Nullraumes der Matrix. Steht der Nullraum senkrecht auf dem Bildraum, so erhält man eine Orthogonalprojektion.
- Beispiel: Es sei
eine
-Matrix und damit selbst nicht invertierbar. Falls der Rang von
gleich
ist, dann ist
invertierbar und die
-Matrix
- idempotent. Diese Matrix wird beispielsweise in der Methode der kleinsten Quadrate verwendet.
- Nilpotente Matrizen
- Eine Matrix
heißt nilpotent, falls eine Potenz
(und damit auch jede höhere Potenz) die Nullmatrix ergibt.
Eigenschaften von Bilinearformen
Im Folgenden sind Eigenschaften von Matrizen aufgelistet, die Eigenschaften der zugehörigen Bilinearform
entsprechen. Trotzdem können diese Eigenschaften für die dargestellten Endomorphismen eine eigenständige Bedeutung besitzen.
- Symmetrische Matrizen
- Eine Matrix
heißt symmetrisch, wenn sie gleich ihrer transponierten Matrix ist:
- Anschaulich gesprochen sind die Einträge symmetrischer Matrizen symmetrisch zur Hauptdiagonalen.
- Beispiel:
- Symmetrische Matrizen entsprechen einerseits symmetrischen Bilinearformen:
- andererseits den selbstadjungierten linearen Abbildungen:
- Hermitesche Matrizen
- Hermitesche Matrizen sind das komplexe Analogon der symmetrischen Matrizen. Sie entsprechen den hermiteschen Sesquilinearformen und den selbstadjungierten Endomorphismen.
- Eine Matrix
ist hermitesch oder selbstadjungiert, wenn gilt:
- Schiefsymmetrische Matrizen
- Eine Matrix
heißt schiefsymmetrisch oder antisymmetrisch, wenn gilt:
- Um diese Bedingung zu erfüllen, müssen alle Einträge der Hauptdiagonale
den Wert Null haben; die restlichen Werte werden an der Hauptdiagonale
gespiegelt und mit
multipliziert.
- Beispiel:
- Schiefsymmetrische Matrizen entsprechen antisymmetrischen Bilinearformen:
- und antiselbstadjungierten Endomorphismen:
- Positiv definite Matrizen
- Eine reelle Matrix ist positiv definit, wenn die zugehörige Bilinearform
positiv definit ist, das heißt, wenn für alle Vektoren
gilt:
- Positiv definite Matrizen definieren verallgemeinerte Skalarprodukte. Hat die Bilinearform keine negativen Werte, heißt die Matrix positiv semidefinit. Analog kann eine Matrix negativ definit beziehungsweise negativ semidefinit heißen, wenn die obige Bilinearform nur negative beziehungsweise keine positiven Werte hat. Matrizen, die keine dieser Eigenschaften erfüllen, heißen indefinit.
Weitere Konstruktionen
Enthält eine Matrix komplexe Zahlen, erhält man die konjugierte Matrix, indem
man ihre Komponenten durch die konjugiert
komplexen Elemente ersetzt. Die adjungierte Matrix (auch hermitesch
konjugierte Matrix) einer Matrix
wird mit
bezeichnet und entspricht der transponierten Matrix, bei der zusätzlich alle
Elemente komplex konjugiert werden.
- Adjunkte oder komplementäre Matrix
Die komplementäre Matrix
einer quadratischen Matrix
setzt sich aus deren Unterdeterminanten zusammen, wobei eine Unterdeterminante
Minor genannt wird. Für die Ermittlung der Unterdeterminanten
werden die
-te
Zeile und
-te
Spalte von
gestrichen. Aus der resultierenden
-Matrix
wird dann die Determinante
berechnet. Die komplementäre Matrix hat dann die Einträge
Diese Matrix wird manchmal auch als Matrix der Kofaktoren bezeichnet.
- Man verwendet die komplementäre Matrix beispielsweise zur Berechnung der
Inversen einer Matrix
, denn nach dem Laplaceschen Entwicklungssatz gilt:
- Damit ist die Inverse
wenn
Eine Übergangs- oder stochastische Matrix ist eine Matrix, deren Einträge alle zwischen 0 und 1 liegen und deren Zeilen bzw. Spaltensummen 1 ergeben. Sie dienen in der Stochastik zur Charakterisierung zeitlich diskreter Markow-Ketten mit endlichem Zustandsraum. Ein Spezialfall hiervon sind die doppelt-stochastischen Matrizen.
Unendlichdimensionale Räume
Für unendlichdimensionale Vektorräume (sogar über Schiefkörpern) gilt,
dass jede lineare Abbildung
eindeutig durch die Bilder
der Elemente
einer Basis
bestimmt ist und diese beliebig gewählt werden und zu einer linearen Abbildung
auf ganz
fortgesetzt werden können. Ist nun
eine Basis von
,
so lässt sich
eindeutig als (endliche) Linearkombination von Basisvektoren schreiben,
d.h., es existieren eindeutige Koeffizienten
für
,
von denen nur endlich viele von null verschieden sind, sodass
.
Dementsprechend lässt sich jede lineare Abbildung als möglicherweise unendliche
Matrix auffassen, wobei jedoch in jeder Spalte (
„nummeriere“ die Spalten und die Spalte zu
bestehe dann aus den von den Elementen von
nummerierten Koordinaten
)
nur endlich viele Einträge von null verschieden sind, und umgekehrt. Die
entsprechend definierte Matrixmultiplikation entspricht wiederum der Komposition
linearer Abbildungen.
In der Funktionalanalysis betrachtet man topologische Vektorräume, d.h. Vektorräume, auf denen man von Konvergenz sprechen und dementsprechend unendliche Summen bilden kann. Auf solchen können Matrizen mit unendlich vielen von null verschiedenen Einträgen in einer Spalte unter Umständen als lineare Abbildungen verstanden werden, wobei auch andere Basis-Begriffe zugrunde liegen.
Einen speziellen Fall bilden Hilberträume.
Seien also
Hilberträume und
Orthonormalbasen
von
bzw.
.
Dann erhält man eine Matrixdarstellung eines linearen
Operators
(für lediglich dicht
definierte Operatoren funktioniert es ebenso, falls der Definitionsbereich
eine Orthonormalbasis besitzt, was im abzählbardimensionalen Fall stets
zutrifft), indem man die Matrixelemente
definiert; dabei ist
das Skalarprodukt im
betrachteten Hilbertraum (im komplexen Fall semilinear im ersten
Argument).
Dieses sogenannte Hilbert-Schmidt-Skalarprodukt lässt sich im unendlichdimensionalen Fall nur noch für eine bestimmte Teilklasse von linearen Operatoren, die sogenannten Hilbert-Schmidt-Operatoren, definieren, bei denen die Reihe, über die dieses Skalarprodukt definiert ist, stets konvergiert.
Literatur
- Günter Gramlich: Lineare Algebra. Fachbuchverlag Leipzig im Carl Hanser Verlag, München u. a. 2003, ISBN 3-446-22122-0.
- Klaus Jänich: Lineare Algebra. 11. Auflage. Springer, Berlin u. a. 2008, ISBN 978-3-540-75501-2.
- Karsten Schmidt, Götz Trenkler: Einführung in die Moderne Matrix-Algebra. Mit Anwendungen in der Statistik. 2., vollständig überarbeitete Auflage. Springer, Berlin u. a. 2006, ISBN 3-540-33007-0.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 19.09. 2021