Dyadisches Produkt
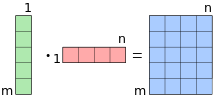
Das dyadische Produkt (kurz auch Dyade von griech. δύας, dýas „Zweiheit“) oder tensorielle Produkt ist in der Mathematik ein spezielles Produkt zweier Vektoren. Das Ergebnis eines dyadischen Produkts ist eine Matrix (oder ein Tensor zweiter Stufe) mit dem Rang eins. Das dyadische Produkt kann als Spezialfall eines Matrizenprodukts einer einspaltigen Matrix mit einer einzeiligen Matrix angesehen werden; es entspricht dann dem Kronecker-Produkt dieser beiden Matrizen. Um den Gegensatz zum inneren Produkt (Skalarprodukt) zu betonen, wird das dyadische Produkt gelegentlich auch äußeres Produkt genannt, wobei diese Bezeichnung aber nicht eindeutig ist, da sie auch für das Kreuzprodukt und das Dachprodukt verwendet wird.
Das Konzept des dyadischen Produkts geht auf den US-amerikanischen Physiker Josiah Willard Gibbs zurück, der es erstmals im Jahr 1881 im Rahmen seiner Vektoranalysis formulierte.
Definition
Das dyadische Produkt ist eine Verknüpfung
zweier reeller Vektoren
und
der Form
,
wobei das Ergebnis eine Matrix
ist. Jeder Eintrag
der Ergebnismatrix berechnet sich dabei aus den Vektoren
und
über
als das Produkt
der Elemente
und
.
Interpretiert man den ersten Vektor als einspaltige Matrix und den zweiten
Vektor als einzeilige Matrix, so lässt sich das dyadische Produkt mittels
als Matrizenprodukt
darstellen, wobei
der zu
transponierte
Vektor ist. Das dyadische Produkt kann so auch als Spezialfall des Kronecker-Produkts
einer einspaltigen mit einer einzeiligen Matrix angesehen werden.
Beispiele
Sind
und
,
dann ist das dyadische Produkt von
und
Jede Spalte dieser Matrix ist also ein Vielfaches
von
und jede Zeile ein Vielfaches von
.
Als triviale
Beispiele sind jede Nullmatrix
das dyadische Produkt von Nullvektoren
und jede Einsmatrix das dyadische
Produkt von Einsvektoren
entsprechend passender Größe:
und
Eigenschaften
Die folgenden Eigenschaften des dyadischen Produkts ergeben sich direkt aus den Eigenschaften der Matrizenmultiplikation.
Kommutativität
Das dyadische Produkt ist, wie zahlreiche Beispiele belegen, nicht kommutativ.
Für die Transponierte des dyadischen Produkts zweier Vektoren
und
gilt
.
Zwei Vektoren
und
sind damit genau dann vertauschbar, das heißt, es gilt
,
wenn die Ergebnismatrix symmetrisch
ist. Dies ist genau dann der Fall, wenn einer der beiden Vektoren ein Vielfaches
des anderen Vektors ist, das heißt, wenn es eine Zahl
gibt, sodass
oder
gilt. Ist einer der Vektoren ein Nullvektor, dann gilt insbesondere für alle
,
wobei die Ergebnismatrix dann die Nullmatrix ist.
Distributivität
Mit der Vektoraddition
ist das dyadische Produkt distributiv,
das heißt, es gilt für alle
und
sowie für alle
und
entsprechend
.
Weiter ist das dyadische Produkt verträglich mit der Skalarmultiplikation,
das heißt für
und
sowie
gilt
.
Dyadisches Produkt zweier Vektoren
Das dyadische Produkt zweier Vektoren
und
ergibt, sofern keiner der beiden Vektoren der Nullvektor ist, eine Rang-Eins-Matrix, das
heißt
.
Umgekehrt lässt sich jede Rang-Eins-Matrix als dyadisches Produkt zweier Vektoren darstellen. Für die Spektralnorm und die Frobeniusnorm eines dyadischen Produkts gilt
,
wobei
die euklidische
Norm des Vektors
ist. Neben der Nullmatrix sind Rang-Eins-Matrizen die einzigen Matrizen, für die
diese beiden Normen übereinstimmen.
Bezüge zu anderen Produkten
Skalarprodukt
Bildet man umgekehrt das Produkt aus einem Zeilenvektor mit einem
Spaltenvektor, so erhält man das Standardskalarprodukt
zweier Vektoren
gegeben durch
,
wobei das Ergebnis eine reelle Zahl ist. Das Standardskalarprodukt zweier Vektoren ist gleich der Spur (der Summe der Diagonalelemente) ihres dyadischen Produkts, also
.
Weiter ist die Matrix
genau dann nilpotent
(immer vom Grad 2), wenn die beiden Vektoren orthogonal
sind, das heißt
.
Wenn sich Zeilen- und Spaltenvektoren passender Größe abwechseln, können auch mehrere Vektoren miteinander multipliziert werden. Aufgrund der Assoziativität der Matrizenmultiplikation erhält man so die Identitäten
und
.
Ein Skalarprodukt
wird auch inneres Produkt genannt, weswegen das dyadische Produkt gelegentlich
auch als äußeres Produkt bezeichnet wird. Diese Dualität wird in der Bra-Ket-Notation der Quantenmechanik
genutzt, wo ein inneres Produkt durch
und ein äußeres Produkt durch
notiert wird.
Tensorprodukt
Der Vektorraum, der durch
dyadische Produkte von Vektoren
aufgespannt wird,
ist der Tensorproduktraum
.
Dieser Raum ist isomorph
zum Raum aller Matrizen .
Jede Matrix
lässt sich demnach als Linearkombination
dyadischer Produkte von Vektoren darstellen, das heißt
,
wobei ,
und
sind. Durch eine geeignete Wahl von Vektoren
und einer Rangschranke
lässt sich auf diese Weise auch eine Niedrigrang-Approximation
einer Matrix erreichen, wodurch numerische
Berechnungen bei sehr großen Matrizen beschleunigt werden können.
Verwendung
In vielen Anwendungen wird ein dyadisches Produkt nicht komponentenweise
ausgerechnet, sondern zunächst stehen gelassen und erst ausgewertet, wenn es mit
weiteren Termen multipliziert wird. Multipliziert man das dyadische Produkt
mit einem Vektor
,
erhält man einen Vektor, der parallel
zu
ist, da
gilt. Das dyadische Produkt eines Einheitsvektors
mit sich selbst ist ein Projektionsoperator,
denn das Matrix-Vektor-Produkt
projiziert einen gegebenen Vektor
orthogonal auf eine Ursprungsgerade
mit Richtungsvektor
.
Die Spiegelung
eines Vektors an einer Ursprungsebene
mit Einheits-Normalenvektor
ergibt sich entsprechend als
,
wobei
die Einheitsmatrix
ist. Solche Spiegelungen werden beispielsweise in der Householdertransformation
verwendet.
Koordinatenfreie Darstellung
In einer abstrakteren, koordinatenfreien Darstellung ist das dyadische
Produkt
zweier Vektoren
und
aus zwei Vektorräumen
und
ein Tensor zweiter Stufe
im Tensorproduktraum
.
Die verschiedenen Notationen verwenden teilweise Fettdruck für Vektoren oder
lassen das Zeichen
weg:
Nicht jeder Tensor zweiter Stufe ist ein dyadisches Produkt von zwei Vektoren, jedoch kann jeder Tensor zweiter Stufe als Summe dyadischer Produkte dargestellt werden. Ein Tensor, der dyadisches Produkt zweier Vektoren ist, heißt einfacher Tensor oder Dyade.
Anwendung findet diese Version des dyadischen Produkts in der Kontinuumsmechanik,
wo meist
identisch mit dem dreidimensionalen Vektorraum
der geometrischen Vektoren ist.
Ist
ein euklidischer
Vektorraum, so kann mit Hilfe des Skalarprodukts „·“ von
das innere Produkt zwischen Tensoren und Vektoren definiert werden. Es ordnet
jedem Tensor
und Vektoren
einen Vektor
zu. Für Dyaden
ist das innere Produkt wie folgt definiert:
Hierdurch kann jede Dyade und damit auch jeder Tensor
als lineare
Abbildung
aufgefasst werden. Der Tensorproduktraum
kann also mit dem Raum
der linearen Abbildungen von
nach
identifiziert werden. Dies wird im Folgenden getan.
Für das dyadische Produkt gelten die folgenden Rechenregeln. ,
,
und
,
seien euklidische Vektorräume. Dann gilt für alle
:
.
Zu beachten ist hier, dass die Skalarprodukte „·“ in den Gleichungen aus den
verschiedenen Vektorräumen stammen, was sich durch einen Index verdeutlicht
beispielsweise wie folgt schreibt: .
Das Skalarprodukt
zweier Tensoren aus
kann mit Vektoren
definiert werden:
Damit baut
einen euklidischen
Vektorraum auf, dessen Elemente Tensoren zweiter Stufe sind. Mit einer Basis
von
und
von
besitzt
eine Basis
bezüglich der jeder Tensor komponentenweise dargestellt werden kann:
worin
die Dimension von
und
die Dimension von
ist. Der Tensor ist von den verwendeten Basen unabhängig. Bei einem Basiswechsel
ändern sich daher die Komponenten
auf charakteristische Weise. Von Bedeutung sind Invarianten, die bei
solchen Basiswechseln ihren Wert nicht ändern, siehe z.B. Hauptinvariante.
Die Komponenten
können in einer Matrix angeordnet werden, wobei dann die verwendete Basis in
Erinnerung behalten werden muss. Gelegentlich wird z.B.
geschrieben. Ist der Definitionsbereich mit dem Bildbereich identisch, kann
bei Verwendung der Standardbasis
der Verweis auf die verwendete Basis weggelassen werden und der Tensor geht in
seine Matrixrepräsentation über, z.B.:
.
In Koordinatendarstellung ist das oben als Matrix definierte dyadische Produkt zweier Spaltenvektoren gerade diese Abbildungsmatrix des Tensors.
Literatur
- Gerd Fischer: Lineare Algebra. 14. Auflage. Vieweg, 2003, ISBN 3-528-03217-0.
- Rudolf Zurmühl: Matrizen und ihre Anwendungen. 7. Auflage. Springer, 1997, ISBN 3-540-61436-2.
- H. Altenbach: Kontinuumsmechanik. Springer Verlag, 2012, ISBN 978-3-642-24118-5.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 28.01. 2021