Ursprungsebene

Eine Ursprungsebene ist in der Mathematik eine Ebene, die den Koordinatenursprung enthält. Wichtige Ursprungsebenen sind die drei Koordinatenebenen in einem kartesischen Koordinatensystem. Ursprungsebenen weisen besonders kompakte Darstellungen als Ebenengleichung auf und zeichnen sich durch vergleichsweise einfache Formeln zur Schnitt- und Abstandsberechnung aus. Die Menge der Vektoren, die in einer Ursprungsebene liegen, bildet einen zweidimensionalen Untervektorraum des dreidimensionalen euklidischen Raums.
Definition
In der analytischen
Geometrie wird eine Ebene
als Teilmenge der Punkte des dreidimensionalen Raums aufgefasst,
wobei jeder Punkt durch seine Koordinaten
dargestellt wird. Eine Ursprungsebene ist nun dadurch ausgezeichnet, dass sie
durch den Koordinatenursprung
des gewählten kartesischen
Koordinatensystems verläuft. In Koordinatenform
wird eine Ursprungsebene dann durch die Ebenengleichung
beschrieben, wobei
und
reelle Parameter sind, die nicht alle gleich null sein dürfen.
Vektordarstellung
Ursprungsebenen können auch durch Vektorgleichungen dargestellt werden, wobei
jeder Punkt der Ebene durch seinen Ortsvektor
dargestellt wird. In Parameterform
wird eine Ursprungsebene dann durch die Gleichung
mit
beschrieben, wobei
und
zwei linear
unabhängige Vektoren der Ebene sind. Eine Ursprungsebene besteht damit aus
denjenigen Punkten, deren Ortsvektoren als Linearkombination
zweier gegebener Vektoren geschrieben werden können. In Normalenform wird eine
Ursprungsebene durch die Normalengleichung
charakterisiert, wobei
ein Normalenvektor
der Ebene ist und
das Skalarprodukt der beiden
Vektoren
und
darstellt. Eine Ursprungsebene besteht damit aus denjenigen Punkten, deren
Ortsvektoren senkrecht
auf einem gegebenen Vektor stehen.
Ist eine Ursprungsebene in Parameterform gegeben, so kann ein Normalenvektor der
Ebene durch das Kreuzprodukt
berechnet werden.
Beispiele
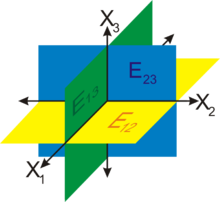
Wichtige Beispiele für Ursprungsebenen sind die drei Koordinatenebenen
bzw.
bzw.
bzw.
bzw.
bzw.
bzw.
Hierbei sind ,
und
die drei Einheitsvektoren.
Eigenschaften
Schnitt
Der Schnitt zweier verschiedener Ursprungsebenen ergibt immer eine Ursprungsgerade, das heißt eine Gerade mit der Geradengleichung
mit
,
wobei
ein Richtungsvektor der Gerade
ist. Besitzen die beiden Ursprungsebenen die Normalenvektoren
und
,
dann ergibt sich ein Richtungsvektor der Schnittgerade als das Kreuzprodukt
der beiden Normalenvektoren. Der Schnitt dreier Ursprungsebenen ergibt genau dann den Koordinatenursprung, wenn ihre Normalenvektoren linear unabhängig sind. Dabei sind drei Vektoren im Raum genau dann linear unabhängig, wenn sie nicht in der gleichen Ursprungsebene liegen.
Abstand eines Punkts
Der Abstand eines Punkts mit
Ortsvektor
von einer Ursprungsebene
mit Normalenvektor
beträgt
,
wobei
die Länge (euklidische
Norm) von
ist. Dieser Abstand entspricht gerade der Länge der Lotstrecke zwischen
dem Punkt und der Ebene. Der Ortsvektor des Lotfußpunkts
ist dann die Orthogonalprojektion
von
auf die Ursprungsebene und somit durch
gegeben.
Spiegelung eines Punkts
Man erhält die Spiegelung
eines Punkts mit Ortsvektor
an einer Ursprungsebene, indem man den Lotvektor
von dem Punkt auf die Ebene verdoppelt. Der bezüglich einer Ursprungsebene
gespiegelte Vektor
eines Vektors
ist damit durch
gegeben, wobei
wieder ein Normalenvektor der Ebene ist.
Vektorraumstruktur
Die Menge der Vektoren des dreidimensionalen Raums bildet einen Vektorraum, den euklidischen Raum. Die Menge der Vektoren, die in einer Ursprungsebene liegen, bildet dabei einen Untervektorraum des euklidischen Raums
.
Dieser Untervektorraum ist gerade die lineare
Hülle der beiden die Ursprungsebene aufspannenden Vektoren
und
,
beziehungsweise der Orthogonalraum
der linearen Hülle eines Normalenvektors
der Ebene. Die Ursprungsebenen sind dabei die einzigen zweidimensionalen
Untervektorräume des euklidischen Raums.
Zu jeder Ebene ,
die nicht den Ursprung enthält, existiert genau eine parallele
Ursprungsebene
.
Jede Ebene
kann damit als affiner
Unterraum des euklidischen Raums der Form
dargestellt werden, wobei
der Ortsvektor eines Punkts von
ist.
Verallgemeinerungen
Allgemeiner können Ebenen auch in höherdimensionalen Räumen betrachtet
werden. Eine Ursprungsebene ist dann ein zweidimensionaler Untervektorraum des
.
In Parameterform ist eine solche Ursprungsebene wie in drei Dimensionen durch
mit
gegeben, wobei
zwei linear unabhängige Vektoren sind. Die entsprechende Normalenform
mit
definiert allerdings für
keine Ebene mehr, sondern eine Hyperebene
der Dimension
,
die den Ursprung enthält.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 07.08. 2021