Projektiver Raum

Der projektive Raum ist ein Begriff aus dem mathematischen Teilgebiet
der Geometrie. Dieser Raum kann
aufgefasst werden als die Menge aller Geraden durch den Ursprung eines Vektorraums .
Ist
der reelle zweidimensionale Vektorraum
so nennt man ihn reelle
projektive Gerade und im Falle
heißt er reelle
projektive Ebene. Analog definiert man projektive Geraden und projektive
Ebenen über beliebigen Körpern als die Mengen der Ursprungsgeraden in einem
zwei- bzw. dreidimensionalen Vektorraum über dem jeweiligen Körper. Projektive
Ebenen können in der Inzidenzgeometrie auch axiomatisch charakterisiert werden,
dabei erhält man auch projektive Ebenen, die nicht den Geraden in einem
Vektorraum entsprechen.
Die Idee der projektiven Räume steht in Beziehung zur Zentralprojektion aus
der darstellenden
Geometrie und Kartenentwurfslehre,
beziehungsweise zur Art und Weise, wie das Auge oder eine Kamera eine
dreidimensionale Szene auf ein zweidimensionales Abbild projiziert. Alle Punkte,
die gemeinsam mit der Linse der Kamera auf einer Linie liegen, werden auf einen
gemeinsamen Punkt projiziert. In diesem Beispiel ist der zugrundeliegende
Vektorraum der ,
die Kameralinse ist der Ursprung und der projektive Raum entspricht den
Bildpunkten.
Definition
Der reell-projektive Raum
ist die Menge aller Geraden durch den Nullpunkt im
.
Formal definiert man dies wie folgt.
Auf
sei die Äquivalenzrelation
definiert. In Worten heißt dies, dass
genau dann äquivalent zu
ist, wenn es ein
gibt, so dass
gilt. Alle Punkte auf einer Ursprungsgeraden
– der Ursprung ist nicht enthalten – werden also miteinander identifiziert und
nicht mehr unterschieden.
Der Quotientenraum
mit der Quotiententopologie
wird reeller,
-dimensionaler
projektiver Raum genannt und mit
notiert.
Im Fall
spricht man von der projektiven
Geraden (auch: projektive Linie) und im Fall
von einer projektiven
Ebene.
Wählt man statt
den komplexen Vektorraum
,
so erhält man mit der analogen Definition mit
den komplex projektiven Raum der (komplexen) Dimension
als den Raum der komplex eindimensionalen Unterräume des
.
Die Koordinaten der Punkte des projektiven Raums, welche ja Äquivalenzklassen
von Punkten
sind, werden durch
notiert und heißen homogene
Koordinaten. (Entsprechend für den komplex-projektiven Raum.) Für
definiert die Abbildung
eine Bijektion zwischen
und
.
Allgemeiner können auch projektive Räume über beliebigen anderen Körpern (an
Stelle von
bzw.
)
konstruiert werden.
Ein allgemeinerer Begriff des projektiven Raumes wird in der synthetischen
Geometrie verwendet, vor allem für den Fall
die projektive
Ebene. Die Axiomatik dieses allgemeineren Begriffes wird im Hauptartikel Projektive
Geometrie dargestellt.
Projektive lineare Gruppe (Kollineationen)
Die projektive
lineare Gruppe
ist die Gruppe der invertierbaren projektiven Abbildungen, sie ist definiert als
Quotient von
unter der Äquivalenzrelation
.
Die Wirkung von
auf
gibt eine wohl-definierte Wirkung von
auf
.
Die den Elementen
entsprechenden Abbildungen
sind projektive, das heißt hier doppelverhältnistreue Kollineationen. Mit
anderen Worten:
- Sie bilden die Menge der projektiven Punkte bijektiv auf sich selbst ab.
- Sie bilden jede Gerade als Punktmenge auf eine Gerade ab (erhalten damit die Inzidenzstruktur).
- Das Doppelverhältnis von beliebigen 4 Punkten, die auf einer Geraden liegen, bleibt unverändert. Das unterscheidet Projektivitäten von bijektiven echt semilinearen Selbstabbildungen des Vektorraums.
Analog definiert man eine Wirkung von
auf
.
Im Fall der projektiven Gerade wirkt
auf
durch gebrochen-lineare Transformationen. Nach der Identifikation von
mit
(bzw.
mit
)
wirkt
bzw.
durch
.
Beispiel: Riemann’sche Zahlenkugel
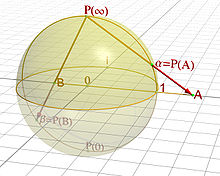
Die komplex-projektive Gerade ist nach obiger Definition gerade die Menge der
komplexen Geraden in ,
welche durch den Ursprung
gehen.
Die komplex-projektive Gerade kann man auch als die reell-zweidimensionale Sphäre beziehungsweise Riemann’sche Zahlenkugel
auffassen. Die Übereinstimmung mit obigen Begriffen ergibt sich wie folgt:
Bezeichne mit
den „Nordpol“. Betrachte die stereographische
Projektion
welche durch
gegeben ist. Anschaulich legt man durch
und den Nordpol eine (reelle) Gerade und wählt den Schnittpunkt dieser Geraden
mit der Äquatorebene als Bildpunkt der Abbildung, wobei der Nordpol mit
identifiziert wird. Die Korrespondenz zwischen
und
in homogenen Koordinaten ist dann
.
Eigenschaften
- Die reellen und komplexen projektiven Räume sind kompakte Mannigfaltigkeiten.
- Der projektive Raum ist ein Beispiel für eine nicht affine algebraische Varietät bzw. ein nicht affines Schema. Außerdem hat der projektive Raum die Struktur einer torischen Varietät. Im algebraisch-geometrischen Kontext kann man anstelle der reellen oder komplexen Zahlen jeden beliebigen Körper einsetzen.
- Untervarietäten des projektiven Raums werden als projektive Varietäten (veraltet auch als projektive Mannigfaltigkeiten) bezeichnet.
- Lokal nach dem projektiven Raum modellierte lokal-homogene Mannigfaltigkeiten werden als projektive Mannigfaltigkeiten bezeichnet.
Topologie
Die projektive Gerade
ist homöomorph
zum Kreis
.
Für
ist die Fundamentalgruppe
des projektiven Raums
die Gruppe Z/2Z,
die 2-fache Überlagerung
des
ist die Sphäre
.
Für ungerade n ist der
orientierbar,
für gerade n ist er nicht orientierbar.
Die projektive Ebene
ist eine nicht-orientierbare Fläche,
die sich nicht in den
einbetten
lässt. Es gibt aber Immersionen des
in den
,
zum Beispiel die sogenannte Boysche
Fläche.
Die komplex-projektive Gerade
ist homöomorph zur Sphäre
,
die quaternionisch-projektive Gerade
ist homöomorph zur
,
die Cayley-projektive Gerade
homöomorph zur
.
Alle komplex- oder quaternionisch-projektiven Räume sind einfach zusammenhängend.
Die Hopf-Faserungen
bilden (für )
jeweils die Einheitssphäre in
auf
ab, die Faser ist die Einheitssphäre in
.
Man erhält auf diese Weise Faserungen
.
Diese Faserungen haben Hopf-Invariante 1.
Projektive Teilräume und abgeleitete Räume
In diesem Abschnitt wird im Sinne der obigen allgemeineren Definition von
einem
dimensionalen projektiven Raum
über einem beliebigen Körper
ausgegangen, die Punkte des Raumes können also als eindimensionale Untervektorräume von
angesehen werden.
- Jedem
-dimensionalen Unterraum
von
ist ein
-dimensionaler projektiver Teilraum
von
zugeordnet. Man nennt
auch eine (verallgemeinerte, projektive) Ebene, für
Hyperebene, für
Gerade in
. Auch die leere Menge wird hier als projektiver Teilraum betrachtet, dem der Nullraum von
und als Dimension
zugeordnet wird.
- Die Schnittmenge von zwei projektiven Teilräumen ist wiederum ein projektiver Teilraum.
- Bildet man zu den Unterräumen, die zwei projektiven Räumen
und
zugeordnet sind, die lineare Hülle ihrer Vereinigungsmenge in
, so gehört zu diesem Untervektorraum wieder ein projektiver Teilraum, der Verbindungsraum
(auch als Summe
notiert) von
und
.
- Für Schnitt und Verbindung von projektiven Teilräumen gilt die projektive Dimensionsformel:
-
.
- Die Menge
aller Teilräume des projektiven Raumes
bildet bezüglich der Verknüpfungen „Schnitt“
und „Verbindung“
einen längenendlichen, modularen, komplementären Verband.
- Jedem projektiven Punkt kann über seine Koordinaten eine homogene
Koordinatengleichung zugeordnet werden, deren Lösungsmenge eine Hyperebene
beschreibt. Durch die so definierten Hyperebenenkoordinaten bilden die
Hyperebenen in
wiederum Punkte eines projektiven Raumes, des Dualraums
.(→ siehe dazu Projektives Koordinatensystem#Koordinatengleichungen und Hyperebenenkoordinaten).
- Allgemeiner bildet die Menge der Hyperebenen, die einen festen
-dimensionalen Teilraum
enthalten, einen projektiven Raum, den man als Bündel, im Spezialfall
als Büschel von Hyperebenen bezeichnet.
heißt Träger des Bündels oder Büschels.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 18.08. 2021