Doppelverhältnis

Das 3. Beispiel zeigt 4 harmonisch liegende Punkte, siehe harmonische Teilung.
Das Doppelverhältnis ist in der Geometrie im einfachsten Fall das
Verhältnis zweier Teilverhältnisse.
Wird zum Beispiel die Strecke
sowohl durch einen Punkt
als auch durch einen Punkt
in jeweils zwei Teilstrecken
und
bzw.
und
(s. erstes Beispiel) geteilt, so ist das Verhältnis
das (affine) Doppelverhältnis, in dem die Teilpunkte
die gegebene Strecke
teilen. Die große Bedeutung erhält das Doppelverhältnis als Invariante bei Zentralprojektionen,
denn das anschaulichere Teilverhältnis ist zwar invariant unter
Parallelprojektionen, aber nicht unter Zentralprojektionen. Eine
Verallgemeinerung führt zur Definition des Doppelverhältnisses für Punkte einer
projektiven Gerade (das heißt, einer affinen Geraden, der ein Fernpunkt
hinzugefügt wird).
Ein besonderer Fall liegt vor, wenn das Doppelverhältnis den Wert −1 annimmt.
In diesem Fall spricht man von einer harmonischen
Teilung der Strecke
durch das Punktepaar
und sagt,
liegen harmonisch.
Während man das Teilverhältnis dreier Punkte noch gut an der Lage der Punkte abschätzen kann, ist dies für das Doppelverhältnis fast unmöglich. Das Doppelverhältnis hat in der analytischen und projektiven Geometrie hauptsächlich theoretische Bedeutung (Invariante bei projektiven Kollineationen). In der Darstellenden Geometrie allerdings wird es (ohne Rechnung) zur Rekonstruktion ebener Figuren verwendet.
Affines Doppelverhältnis
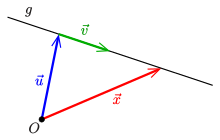
Eine Gerade im affinen
Raum
lässt sich mit zwei fest gewählten Vektoren
durch
parametrisieren. Für vier Punkte
einer Geraden
seien
die Parameter bezüglich der Parameterdarstellung
der Geraden
.
Dann heißt das Verhältnis der Teilverhältnisse
das affine Doppelverhältnis der Punkte .
Eigenschaften
Liegen beide Teilpunkte
zwischen
(innere Teilungen) oder beide außerhalb, so ist das Doppelverhältnis
positiv, in den anderen Fällen (ein Teilpunkt innen, der andere außen)
ist das Doppelverhältnis negativ.
Harmonischer Punkt
Ist das Doppelverhältnis ,
so sagt man
liegen harmonisch. Siehe Harmonische
Teilung.
Beispiele
Haben
die Parameter
,
so ist
.
- Für
ist das Doppelverhältnis
(siehe Bild in der Einleitung).
- Liegen
harmonisch, so gilt:
, d.h., das harmonische Mittel der Zahlen
ist
.
Doppelverhältnis
Das „normale“ Doppelverhältnis wird für vier Punkte auf einer projektiven Gerade erklärt.
Projektive Gerade
Eine projektive
Gerade über einem Körper
ist die Menge der eindimensionalen Unterräume
in einem zweidimensionalen
-Vektorraum.
Nach Wahl einer Basis
sind die Punkte der projektiven Geraden dann durch homogene Koordinaten
mit
gegeben, wobei der Punkt mit homogenen Koordinaten
dem eindimensionalen Unterraum
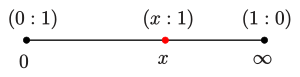
entspricht und demzufolge
für alle
ist. Man kann die projektive Gerade
auch mit
identifizieren, dabei werden homogene Koordinaten in inhomogene Koordinaten
übergeführt:
entspricht dem Punkt
und
dem Punkt
.
Das Doppelverhältnis
Für vier Punkte
einer projektiven Geraden
mit den zugehörigen homogenen Koordinaten
heißt
das Doppelverhältnis von .
Eigenschaften des Doppelverhältnisses:
(Vertauschen von
)
(Vertauschen von
)
- Das Doppelverhältnis ist gegenüber einem Basiswechsel invariant (siehe Regeln für Determinanten).
- Sind die vier Punkte vom Fernpunkt
verschieden, lassen sie sich mit homogenen Koordinaten so beschreiben, dass
ist. In diesem Fall ergibt sich das (affine) Doppelverhältnis (s.o.)

Invarianz des Doppelverhältnisses
In einer projektiven Koordinatenebene über einem Körper sind die projektiven
Kollineationen diejenigen Kollineationen, die von linearen Abbildungen erzeugt
werden. Da bei geeigneter Koordinatisierung vier kollineare Punkte
immer so beschrieben werden können, dass
ist und eine lineare Abbildung den Faktor
invariant lässt, bleibt damit auch das Doppelverhältnis
invariant.
In der Darstellenden Geometrie werden Geraden des Raumes mit einer Zentralprojektion in eine Bildtafel projiziert. So eine Zentralprojektion lässt sich zu einer projektiven Kollineation des Raumes fortsetzen und projektive Kollineationen lassen das Doppelverhältnis invariant. Also gilt:
- Das Doppelverhältnis bleibt bei einer Zentralprojektion invariant. (s. Bild)
Doppelverhältnis von 4 kopunktalen Geraden

Wegen der Invarianz des Doppelverhältnisses bei Zentralprojektion lässt es sich auch für vier in einer Ebene liegende kopunktale Geraden erklären:
- Das Doppelverhältnis von vier kopunktalen Geraden einer Ebene ist
das Doppelverhältnis der vier Punkte
einer die 4 Geraden schneidenden Geraden (s. Bild).
Da der Betrag einer (2 × 2)-Determinante gleich dem doppelten Flächeninhalt
des Dreiecks, das von den Spaltenvektoren aufgespannt wird, ist und der
Flächeninhalt eines Dreiecks durch
(
sind Seiten des Dreiecks und
der eingeschlossenen Winkel, siehe Dreiecksfläche)
ausgedrückt werden kann, lässt sich das Doppelverhältnis auch wie folgt
beschreiben:
(siehe Bild).
(Die Seitenlängen kürzen sich alle heraus!)
Projektive Geometrie
In einem projektiven Raum kann das Doppelverhältnis aus den projektiven Koordinaten der vier kollinearen Punkte berechnet werden, dabei ist es von der speziellen Wahl des Koordinatensystems unabhängig. Umgekehrt können projektive Koordinaten als Doppelverhältnisse aufgefasst werden. → Siehe dazu Projektives Koordinatensystem.
Das Doppelverhältnis ist eine Invariante jeder projektiven Abbildung, d.h., es behält bei Anwendung einer solchen Abbildung seinen Wert. Diese Eigenschaft kann als kennzeichnendes Merkmal der projektiven Geometrie angesehen werden. Siehe dazu: Erlanger Programm. Diese Zusammenhänge waren schon im Altertum bekannt und finden sich z.B. bei Pappos. Sie sind der entscheidende Grund dafür, dass der Begriff Doppelverhältnis überhaupt entwickelt wurde.
Doppelverhältnis und hyperbolischer Abstand
Die reelle projektive Gerade ist der Rand im Unendlichen der hyperbolischen Ebene. Der hyperbolische Abstand lässt sich aus dem Doppelverhältnis rekonstruieren wie folgt.
Für zwei Punkte
und
der hyperbolischen Ebene sei
die (eindeutig bestimmte) durch diese beiden Punkte verlaufende Geodätische und
seien deren Endpunkte im Unendlichen. Seien
die durch
bzw.
verlaufenden Horosphären
mit Mittelpunkt
und seien
die Mittelpunkte der beiden zu
und
tangentialen Horosphären. Dann kann der hyperbolische Abstand berechnet werden
durch
.
Umgekehrt kann das Doppelverhältnis aus dem hyperbolischen Abstand rekonstruiert werden durch die Formel
wobei die Konvergenz
entlang einer Geodätischen erfolgt.
Diese Formel erlaubt eine direkte Verallgemeinerung des Doppelverhältnisses für 4-Tupel von Punkten im Unendlichen eines beliebigen CAT(-1)-Raumes, insbesondere einer Hadamard-Mannigfaltigkeit negativer Schnittkrümmung.
Geschichte
Das Doppelverhältnis und seine Invarianz unter Projektivitäten wurde in der Antike von Pappos verwendet und um 1640 von Gérard Desargues wiederentdeckt. Es wurde zu einem Standardwerkzeug in der Blüte der projektiven Geometrie im 19. Jahrhundert. Arthur Cayley benutzte es 1859 in Sixth memoir on quantics zur Definition einer Metrik in der projektiven Geometrie. Felix Klein bemerkte 1871 in Ueber die sogenannte Nicht-Euclidische Geometrie, dass man auf diese Weise die hyperbolische Metrik der Kreisscheibe erhält.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 23.06. 2021