
Teilverhältnis

Unter dem Teilverhältnis versteht man in der Geometrie im einfachsten Fall
das Verhältnis zweier Teilstrecken einer gegebenen Strecke. Wird z.B. die
Strecke
durch einen Punkt
in zwei Teilstrecken
und
geteilt (s. erstes Beispiel), so ist die Zahl
das zugehörige Teilverhältnis. Man könnte allerdings auch den Kehrwert, der
durch Vertauschen von
und
entsteht, als Teilverhältnis erklären. Beim Umgang mit Teilverhältnissen ist
also unbedingt auf die Bezeichnung der Punkte zu achten.
Die große Bedeutung erhält das Teilverhältnis durch die Verallgemeinerung auf
beliebige Teilpunkte
auf der Geraden durch
.
Die große Bedeutung des Teilverhältnisses liegt in seiner Invarianz unter affinen Abbildungen (lineare Abbildungen und Translationen) und Parallelprojektionen. Bei projektiven Abbildungen und Zentralprojektionen bleibt das Teilverhältnis im Allgemeinen nicht invariant, aber das sogenannte Doppelverhältnis.
Definition
In der Literatur findet man die folgende Definition für drei Punkte in der euklidischen Ebene:
- Für drei verschiedene kollineare
Punkte
nennt man die Zahl
mit der Eigenschaft
-
- das Teilverhältnis, in dem der Punkt
das Punktepaar
teilt, und bezeichnet sie mit
oder
.
Der Fall
lässt sich mit einbeziehen und liefert
.
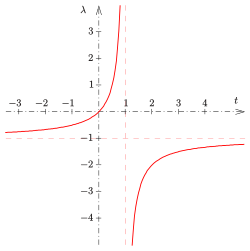
Das Teilverhältnis kann jede reelle Zahl außer −1 annehmen (s. u.).
Das Wort „teilt“ darf man nach der Ausdehnung auf beliebige Punkte
nicht zu wörtlich nehmen, denn nur, wenn
zwischen
liegt, teilt
die Strecke
.
Es gilt:
- Liegt
zwischen
und
, so ist
und man spricht von einer inneren Teilung.
- Liegt
außerhalb, so ist
und man spricht von einer äußeren Teilung. Falls
außerhalb auf der Seite von
liegt, so ist
. Falls
auf der Seite von
liegt, gilt
.
- Nähert sich
von innen
an, so strebt
gegen
, im anderen Fall (von außen) geht
gegen
.
- Falls
der Mittelpunkt der Strecke
ist, ergibt sich
.
Man beachte, dass eine Vertauschung von
das Teilverhältnis verändert (invertiert), außer im Fall, dass
der Mittelpunkt der Strecke ist.
Berechnung des Teilverhältnisses bzw. des Teilpunktes
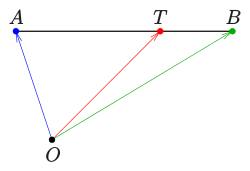
Der Punkt
der Geraden durch die Punkte
und
lässt sich durch
mit einem Parameter
beschreiben.
Aus
und
ergibt sich die Gleichung
und schließlich
.
Löst man die letzte Gleichung nach t auf, so erhält man
und damit zu vorgegebenem Teilverhältnis
den Teilpunkt
mit
Für
ist
und
der Mittelpunkt der Strecke
.
Bemerkung:
Falls die Punkte
durch ihre Parameter
bezüglich einer Parameterdarstellung
der zugrunde liegenden Gerade gegeben sind, ergibt sich für ihr Teilverhältnis
und für die Umkehrung
.
Zeichnerisches Ermitteln des Teilpunkts

Um den Teilpunkt zu finden, verwendet man eine Konstruktion nach dem zweiten Strahlensatz: Soll die Strecke [AB] im Verhältnis m:n geteilt werden, so zeichnet man durch A und durch B zwei parallele Geraden. Auf der Parallelen durch A trägt man m-mal, auf der Parallelen durch B n-mal die gleiche Strecke ab. Bei innerer Teilung muss das Abtragen in verschiedener Richtung, bei äußerer Teilung in gleicher Richtung erfolgen. Man zeichnet die Gerade durch die Endpunkte der abgetragenen Strecken. Ihr Schnittpunkt mit der Geraden AB ist der gesuchte Teilpunkt (S bzw. T).
Invarianz des Teilverhältnisses
Eine beliebige affine Abbildung der reellen Koordinatenebene lässt sich folgendermaßen darstellen:
, wobei
eine lineare Abbildung ist.
Also wird
auf
abgebildet. Hieraus ergibt sich
, die Invarianz des Teilverhältnisses.
Eine Parallelprojektion lässt sich als affine Abbildung oder, bei geeigneter Koordinatisierung, sogar als lineare Abbildung darstellen. Also ist das Teilverhältnis auch bei Parallelprojektion invariant.
Verallgemeinerung
Da zur Definition des Teilverhältnisses nur Zahlen und Vektoren verwendet
wurden, lässt sie sich wörtlich auf eine affine Koordinaten-Ebene über einem
beliebigen Körper
ausdehnen.( Die reellen Zahlen werden als Koordinatenbereich einfach durch einen
beliebigen Körper ersetzt.) Allerdings gelten die obigen Aussagen, die typische
Eigenschaften der reellen Zahlen (""
und "
")
verwenden, nicht mehr. Die Invarianz des Teilverhältnisses gilt auch in diesem
allgemeinen Fall.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 11.02. 2020