Geodäte

Kürzeste Verbindung (Geodäte) auf der Erdkugel

Eine Geodäte (Pl. Geodäten), auch Geodätische, geodätische Linie oder geodätischer Weg genannt, ist die lokal kürzeste Verbindungskurve zweier Punkte. Geodäten sind Lösungen einer gewöhnlichen Differentialgleichung zweiter Ordnung, der Geodätengleichung.

Lokale und globale Definition

Im euklidischen Raum sind Geodäten stets Geraden. Relevant ist der Begriff „Geodäte“ erst in gekrümmten Räumen (Mannigfaltigkeiten), wie zum Beispiel auf einer Kugeloberfläche oder anderen gekrümmten Flächen oder auch in der gekrümmten Raumzeit der allgemeinen Relativitätstheorie. Man findet die geodätischen Linien mit Hilfe der Variationsrechnung.

Die Einschränkung lokal in der Definition bedeutet, dass eine Geodäte nur dann die kürzeste Verbindung zwischen zwei Punkten zu sein braucht, wenn diese Punkte nahe genug beieinander liegen; sie muss aber nicht den global kürzesten Weg darstellen. Jenseits des Schnittortes können mehrere Geodäten unterschiedlicher Länge zum gleichen Punkt führen, was die globale Minimierung der Länge verhindert. Beispielsweise ist die kürzeste Verbindung zwischen zwei nicht-antipodalen Punkten auf einer Kugel stets Teil eines eindeutigen Großkreises, aber die beiden Teile, in die dieser Großkreis durch diese zwei Punkte unterteilt wird, sind beide Geodäten, obwohl nur einer der beiden die global kürzeste Verbindung darstellt.

Beispiele für Geodäten verschiedener Räume

Im $\mathbb {R} ^{n}$ mit euklidischer Metrik sind genau die geraden Strecken die Geodätischen.
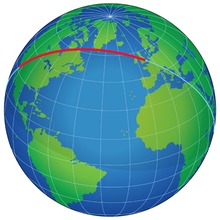
Eine Geodätische auf der Sphäre ist stets Teil eines Großkreises; daran orientieren sich transkontinentale Flug- und Schifffahrtsrouten (siehe Orthodrome). Alle geodätischen Linien (bzw. Großkreise) auf einer Kugel sind in sich geschlossen – das heißt, wenn man ihnen folgt, erreicht man irgendwann wieder den Ausgangspunkt. Auf Ellipsoid-Flächen dagegen gilt dies lediglich entlang der Meridiane und des Äquators (welche auf dem Ellipsoid einfache Spezialfälle der geodätischen Linie sind).
Im Sonderfall abwickelbarer Flächen (z.B. Kegel oder Zylinder) sind die Geodäten diejenigen Kurven, die bei der Abwicklung in die Ebene zu Geradenstücken werden.

Klassische Differentialgeometrie

Geodätische (rot) in einem zweidimensionalen, gekrümmten Raum, der in einen dreidimensionalen Raum eingebettet ist. (Modellierung der Gravitation über die Geodäten in der Relativitätstheorie)

In der klassischen Differentialgeometrie ist eine Geodätische ein Weg $\gamma \colon I\to S$ auf einer Fläche $S\subset \mathbb {R} ^{3}$ , bei dem überall die Hauptnormale mit der Flächennormale zusammenfällt. Diese Bedingung ist genau dann erfüllt, wenn in jedem Punkt die geodätische Krümmung gleich 0 ist.

Riemannsche Geometrie

In der riemannschen Geometrie ist eine Geodätische durch eine gewöhnliche Differentialgleichung charakterisiert. Sei eine riemannsche Mannigfaltigkeit. Eine Kurve $\gamma \colon I\to M$ heißt Geodäte, wenn sie die geodätische Differentialgleichung (Geodätengleichung)

$\nabla _{\dot {\gamma }}{\dot {\gamma }}=0$

erfüllt. Dabei bezeichnet $\nabla$ den Levi-Civita-Zusammenhang. Diese Gleichung bedeutet, dass das Geschwindigkeitsvektorfeld der Kurve längs der Kurve konstant ist. Dieser Definition liegt die Überlegung zu Grunde, dass die Geodätischen des $\mathbb {R} ^{n}$ genau die geraden Linien sind und deren zweite Ableitung konstant null ist.

Ist (U,x) eine Karte der Mannigfaltigkeit, so erhält man mit Hilfe der Christoffelsymbole $\Gamma _{kl}^{m}$ die lokale Darstellung

${\ddot {x}}^{m}+\Gamma _{kl}^{m}{\dot {x}}^{k}{\dot {x}}^{l}=0$

der geodätischen Differentialgleichung. Hier wird die Einsteinsche Summenkonvention verwendet. Die $x^{m}$ sind die Koordinatenfunktionen der Kurve $\gamma$ : Der Kurvenpunkt $\gamma (t)$ hat die Koordinaten $(x^{1}(t),\dots ,x^{n}(t))$ .

Aus der Theorie über gewöhnliche Differentialgleichungen lässt sich beweisen, dass es eine eindeutige Lösung der geodätischen Differentialgleichung mit den Anfangsbedingungen $\gamma (t_{0})=p$ und ${\dot {\gamma }}(t_{0})=V\in T_{p}M$ gibt. Und mit Hilfe der ersten Variation von $\gamma$ lässt sich zeigen, dass die bezüglich des riemannschen Abstands d(.,.) kürzesten Kurven die geodätische Differentialgleichung erfüllen. Umgekehrt kann man zeigen, dass jede Geodätische zumindest lokal eine kürzeste Verbindung ist. Das heißt, auf einer Geodätischen gibt es einen Punkt, ab der die Geodätische nicht mehr die kürzeste Verbindung ist. Ist die zugrundeliegende Mannigfaltigkeit nicht kompakt, so kann der Punkt auch unendlich sein. Fixiert man einen Punkt und betrachtet alle Geodätischen mit Einheitsgeschwindigkeit, die von diesem Punkt ausgehen, so heißt die Vereinigung aller Schnittpunkte der Schnittort. Eine Geodätische mit Einheitsgeschwindigkeit ist eine Geodätische $\gamma$ , für die $\|{\dot {\gamma }}\|=1$ gilt.

Im Allgemeinen muss eine Geodäte nur auf einem Zeitintervall $(-\epsilon ,\epsilon )$ für ein passendes $\epsilon >0$ definiert sein. Eine Riemannsche Mannigfaltigkeit heißt geodätisch vollständig, wenn für jeden Punkt $p\in M$ und jeden Tangentialvektor $v\in T_{p}M$ die Geodäte $\gamma$ mit $\gamma (0)=p$ und ${\dot {\gamma }}(0)=v$ auf ganz $\mathbb {R}$ definiert ist. Der Satz von Hopf-Rinow gibt verschiedene äquivalente Charakterisierungen geodätisch vollständiger Riemannscher Mannigfaltigkeiten.

Im Allgemeinen ist eine Geodäte (im oben definierten Sinn der Riemannschen Geometrie) nur lokal, aber nicht global minimierend. Das heißt, $\gamma$ muss nicht unbedingt die kürzeste Verbindung zwischen $\gamma (0)$ und $\gamma (t)$ für alle sein, es gibt aber ein $\delta >0$ , so dass $\gamma$ für alle $t\in \left[-\delta ,\delta \right]$ die kürzeste Verbindung zwischen $\gamma (0)$ und $\gamma (t)$ ist.

Eine Geodäte heißt minimierende Geodäte, wenn $\gamma$ für alle die kürzeste Verbindung zwischen $\gamma (0)$ und $\gamma (t)$ ist.

Metrische Räume

→ Hauptartikel: Geodätischer metrischer Raum

Sei (X,d) ein metrischer Raum. Für eine Kurve, das heißt eine stetige Abbildung $\gamma \colon \left[a,b\right]\rightarrow X$ , definiert man ihre Länge durch

$L(\gamma )=\sup _{a=t_{0}<t_{1}<\cdots <t_{n}=b}\sum _{i=0}^{n-1}d(\gamma (t_{i}),\gamma (t_{i+1}))$ .

Aus der Dreiecksungleichung folgt die Ungleichung $L(\gamma )\geq d(\gamma (a),\gamma (b))$ .

Als minimierende Geodäte in (X,d) bezeichnet man eine Kurve $\gamma \colon \left[a,b\right]\rightarrow X$ mit $L(\gamma )=d(\gamma (a),\gamma (b))$ , das heißt eine Kurve, deren Länge den Abstand ihrer Endpunkte realisiert. (Geodäten im Sinne der Riemannschen Geometrie müssen nicht immer minimierende Geodäten sein, sie sind es aber „lokal“.)

Ein metrischer Raum (X,d) heißt geodätischer metrischer Raum oder Längenraum, wenn sich je zwei Punkte durch eine minimierende Geodäte verbinden lassen. Vollständige Riemannsche Mannigfaltigkeiten sind Längenräume. Der $\mathbb {R} ^{2}\setminus \left\{(0,0)\right\}$ mit der euklidischen Metrik ist ein Beispiel für einen metrischen Raum, der kein Längenraum ist.

Basierend auf einem Artikel in:

Wikipedia.de