Projektives Koordinatensystem

Ein projektives Koordinatensystem erlaubt es, die Lage eines Punktes in einem projektiven Raum eindeutig durch die Angabe eines Koordinatenvektors zu beschreiben. Dadurch können in den mathematischen Gebieten der Geometrie und der linearen Algebra die strukturerhaltenden Abbildungen von projektiven Räumen (das sind die Kollineationen und vor allem die projektiven Abbildungen) durch koordinatenbezogene Abbildungsmatrizen dargestellt und die Räume mit Methoden der analytischen Geometrie untersucht werden.

Die Komponenten des Koordinatenvektors, der einen Punkt im projektiven Raum beschreibt, heißen projektive Koordinaten. Sie werden auch als homogene Koordinaten bezeichnet. (→ im Hauptartikel „Homogene Koordinaten“ wird auch erläutert, wie projektive Koordinaten zur Kennzeichnung von Elementen verwandter Strukturen wie affiner Räume verwendet werden können.)

In einem abstrakten projektiven Raum endlicher Dimension ist das Koordinatensystem durch n+2 geeignet gewählte Basispunkte bestimmt – die Punkte müssen in allgemeiner Lage gewählt sein und werden dann als projektive Basis bezeichnet. Der Bezug auf Basispunkte an Stelle einer Vektorraumbasis (Hamelbasis), die im Standardmodell völlig ausreicht, ermöglicht eine modellunabhängige geometrische Beschreibung des Bezugssystems und in der synthetischen Geometrie die Einführung vergleichbarer Koordinaten auch in allgemeineren Strukturen (insbesondere projektiven Inzidenzebenen), denen kein Vektorraum und damit kein Körper als Koordinatenbereich zugeordnet werden kann.

Projektive Koordinaten im Standardmodell

Es sei $KP^{n}$ der -dimensionale projektive Raum über dem Körper .

Die projektiven Punkte, die zu einer Vektorraumbasis ${\mathcal {B}}=({\vec {e}}_{0},{\vec {e}}_{1},\ldots ,{\vec {e}}_{n})$ des $K^{{n+1}}$ gehören, also die von diesen Basisvektoren erzeugten eindimensionalen Unterräume

$B_{j}=\lbrace r\cdot {\vec {e_{j}}}:\;r\in K\rbrace ;\quad 0\leq j\leq n$

bilden zusammen mit dem Einheitspunkt

$E=B_{{n+1}}=\lbrace r\cdot \left({\vec {e}}_{0}+{\vec {e}}_{1}+\cdots {\vec {e}}_{n}\right):\;r\in K\rbrace$

eine projektive Basis (auch: projektive Punktbasis) ${\mathcal {B}}_{p}=(B_{0},B_{1},\ldots ,B_{n},B_{{n+1}})$ des projektiven Raumes $KP^{n}$ .

Durch Schlitzen entlang der durch $B_{1},\ldots ,B_{n}$ verlaufenden projektiven Hyperebene erhält man einen affinen Raum ${\mathcal A}$ . In diesem sei der Nullpunkt. Wir betrachten für $i=1,\ldots,n$ den Schnittpunkt $E_{i}$ der Geraden $EB_{i}$ mit der Hyperebene durch $B_{0},\ldots ,B_{{i-1}},B_{{i+1}},\ldots ,B_{n}$ . Diese Punkte $\left\{E_{1},\ldots ,E_{n}\right\}$ bilden mit dem Nullpunkt eine affine Basis von ${\mathcal A}$ . Mit dieser Basis können wir affine Koordinaten $(x_{1},\ldots ,x_{n})$ in ${\mathcal A}$ definieren und die projektiven Koordinaten bezüglich der gewählten projektiven Basis sind dann per Definition $(1;x_{1};\ldots ;x_{n})$ .

Beispiel

Es wird der Raum $KP^{2}$ mit der Standardbasis

$B_{0}=\left[1:0:0\right],B_{1}=\left[0:1:0\right],B_{2}=\left[0:0:1\right],B_{3}=\left[1:1:1\right]$

betrachtet. Dann haben die projektiven Geraden

$B_{3}B_{1}=\left\{\left[1:1+s:1\right]\mid s\in K\right\}\cup \left\{B_{1}\right\}$ und $B_{0}B_{2}=\left\{\left[t:0:1-t\right]\mid t\in K\right\}$

den Schnittpunkt $E_{1}=\left[1:0:1\right]$ und die projektiven Geraden

$B_{3}B_{2}=\left\{\left[1:1:1+s\right]\mid s\in K\right\}\cup \left\{B_{2}\right\}$ und $B_{0}B_{1}=\left\{\left[t:1-t:0\right]\mid t\in K\right\}$

den Schnittpunkt $E_{2}=\left[1:1:0\right]$ . Die projektiven Koordinaten des Punktes $\left[x:y:z\right]$ sind dann $(1;{\tfrac {y}{x}};{\tfrac {z}{x}})$ für $x\not =0$ .

Projektive Koordinaten in der synthetischen Geometrie

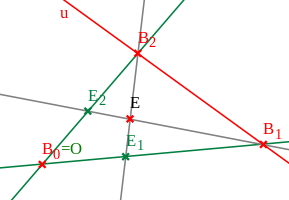
Eine projektive Punktbasis $(B_{0},B_{1},B_{2},E)$ (rot) bestimmt eine eindeutige affine Punktbasis $(O=B_{0},E_{1},E_{2})$ (grün), wobei die Verbindungsgerade $u=B_{1}B_{2}$ zur Ferngeraden wird.

In einer beliebigen, auch nichtdesargueschen projektiven Ebene können projektive Koordinaten nach Wahl einer projektiven Basis mit Hilfe affiner Koordinaten eingeführt werden.

In der projektiven Ebene muss zunächst eine rojektive Basis $(B_{0},B_{1},B_{2},E)$ gewählt worden sein, das heißt, keine drei der vier Punkte sollen auf einer gemeinsamen Geraden liegen. Der Punkt $B_{0}$ wird zum Ursprung $O=B_{0}$ des affinen Koordinatensystems, die Verbindungsgerade $B_{0}B_{1}$ zu seiner ersten, $B_{0}B_{2}$ zu seiner zweiten Koordinatenachse. Die zunächst noch projektiven Schnittpunkte $E_{1}=EB_{2}\cap OB_{1}$ und $E_{2}=EB_{1}\cap OB_{2}$ sind die Einheitspunkte auf diesen Achsen, somit ist (O,E_1,E_2) eine affine Punktbasis der affinen Ebene, die aus der projektiven durch Schlitzen längs der Gerade $u=B_{1}B_{2}$ entsteht. Diese Gerade wird zur Ferngerade der affinen Ebene, siehe dazu auch die Abbildung rechts.

Für jeden Punkt der geschlitzten Ebene können durch Koordinatenkonstruktion affine Koordinaten $(x_{1};x_{2})\in K^{2}$ bestimmt werden, wobei der Koordinatenbereich durch die erste Achse des affinen Koordinatensystems repräsentiert wird. → Die Koordinatenkonstruktion ist im Artikel Ternärkörper beschrieben.
Ein Punkt außerhalb von mit den affinen Koordinaten $(x_{1};x_{2})$ erhält die projektiven Koordinaten $(1;x_{1};x_{2})$ .
Ein Punkt auf der Ferngeraden erhält die projektiven Koordinaten $(0;x_{1};x_{2})$ , wobei $(x_{1};x_{2})$ die affinen Koordinaten des Punktes auf der Verbindungsgerade sind. (Aus der vorausgesetzten "allgemeinen Lage" folgt $O\not \in u$ und mithin $U\not =O$ .)

Die so bestimmten Koordinaten sind für Punkte außerhalb von eindeutig, für Punkte auf kann diese Eindeutigkeit durch zusätzliche Vereinbarungen erreicht werden. Sie sind im Allgemeinen nicht homogen: Im Koordinatenbereich , der ein Ternärkörper ist, lässt sich im Allgemeinen keine „Skalarmultiplikation“ definieren.

Anwendungen

Abbildungen

Wenn und projektive Räume der Dimension bzw. über einem festen Körper sind, dann gilt:

Jede projektive Abbildung $\pi$ von nach besitzt bezüglich fest gewählter projektiver Punktbasen in und eine Darstellung $\pi :\left[x_{0},\ldots ,x_{n}\right]^{T}\rightarrow \left[(A\cdot (x_{0},\ldots ,x_{n})^{T})\right]^{T}$ . Die Abbildungsmatrix hat Zeilen und Spalten und ist bis auf einen skalaren Faktor $r\in K\setminus \lbrace {0}\rbrace$ eindeutig bestimmt.
Wählt man zu jedem Punkt $B_{j}(0\leq j\leq n+1)$ einer projektiven Punktbasis von oder gleichwertig zu Punkten in allgemeiner Lage, jeweils einen beliebigen Bildpunkt $C_{j}\in Q$ , dann lässt sich dies eindeutig zu einer projektiven Abbildung $\pi :P\rightarrow Q$ fortsetzen, bei der also $\pi (B_{j})=C_{j}$ für jeden Basispunkt gilt.
Jede Projektivität $\pi$ auf besitzt bezüglich einer fest gewählten projektiven Punktbasis in eine Darstellung $\pi :\left[x_{0},\ldots ,x_{n}\right]^{T}\rightarrow \left[(A\cdot (x_{0},\ldots ,x_{n})^{T})\right]^{T}$ . Die quadratische, reguläre $(n+1)\times (n+1)$ Abbildungsmatrix ist bis auf einen skalaren Faktor $r\in K\setminus \lbrace {0}\rbrace$ eindeutig bestimmt.
Zu Urbildpunkten $B_{j}(0\leq j\leq n+1)$ in allgemeiner Lage und Bildpunkten $C_{j}(0\leq j\leq n+1)$ in allgemeiner Lage gibt es genau eine Projektivität $\pi$ auf , bei der $\pi (B_{j})=C_{j},(0\leq j\leq n+1)$ ist. Man sagt daher auch, die projektive lineare Gruppe $\operatorname {PGL}(n+1,K)$ operiert scharf einfach transitiv auf der Menge der -Tupel von Punkten in allgemeiner Lage.
Ist die Dimension $n\geq 2$ , dann lässt sich jede Kollineation $\kappa$ auf bezüglich einer fest gewählten projektiven Basis in als Komposition $\kappa =\pi \circ \sigma$ mit einer Projektivität $\pi$ und einem Automorphismus $\sigma$ des Körpers darstellen.

Doppelverhältnis

Das Doppelverhältnis von vier kollinearen Punkten P,Q,R,S in einem projektiven Raum ist das einfache Verhältnis der projektiven Koordinaten, die der Punkt hat, wenn die übrigen drei Punkte als Punktbasis der gemeinsamen Geraden gewählt werden. Dabei sind $B_{0}=R,\,B_{1}=S$ die Basispunkte und $E=B_{2}=Q$ der Einheitspunkt des Koordinatensystems. Hat nun bezüglich dieses Systems die Koordinatendarstellung $P=\left[p_{0};p_{1}\right]$ , dann gilt für das Doppelverhältnis: $t=\operatorname {DV}(PQRS)={\tfrac {p_{1}}{p_{0}}}$ . Dieser Zusammenhang ist einer der Gründe dafür, dass das Doppelverhältnis $t\in K\cup \lbrace \infty \rbrace$ auch gelegentlich als inhomogene projektive Koordinate von (bezüglich der anderen Punkte im Doppelverhältnis) bezeichnet wird.

Parametergleichungen

Die Verbindungsgerade von zwei verschiedenen Punkten $A=\left[a_{0};a_{1};\ldots a_{n}\right]$ und $B=\left[b_{0};b_{1};\ldots b_{n}\right]$ hat die homogene Parameterdarstellung

$\langle A,B\rangle :\;{\vec {x}}=\alpha \cdot {\begin{pmatrix}a_{0}\\a_{1}\\\vdots \\a_{n}\end{pmatrix}}+\beta \cdot {\begin{pmatrix}b_{0}\\b_{1}\\\vdots \\b_{n}\end{pmatrix}}$

Dabei sind dann ${\vec {x}}$ für $(\alpha ;\beta )\in K^{2}\setminus \lbrace 0\rbrace$ die projektiven Koordinaten eines Geradenpunktes $X=\left[{\vec {x}}^{{\,T}}\right]$

Allgemeiner ist der Verbindungsraum von Punkten $A_{j}=\left[{{\vec {a}}_{j}}^{{T}}\right];\;1\leq j\leq k$ , deren Koordinatenvektoren linear unabhängig sind, ein -dimensionaler Unterraum des projektiven Raumes mit der Parameterdarstellung

$\langle A_{1},A_{2},\ldots A_{k}\rangle :{\vec {x}}=\sum _{{j=1}}^{k}\alpha _{j}{\vec {a}}_{j};\quad (\alpha _{1},\alpha _{2},\ldots \alpha _{k})\in K^{k}\setminus \lbrace 0\rbrace .$

Koordinatengleichungen und Hyperebenenkoordinaten

Nach der Wahl einer projektiven Punktbasis ${\mathcal {B}}_{p}$ in einem -dimensionalen projektiven Raum $\mathcal{P}$ kann man jedem Punkt $P=\left[p_{0};p_{1};\ldots p_{n}\right]$ eindeutig die Koordinatengleichung $p_{0}\cdot x_{0}+p_{1}\cdot x_{1}+\cdots +p_{n}\cdot x_{n}=0\;$ zuordnen, deren Lösungsmenge, als Punktkoordinaten aufgefasst, einen n-1 -dimensionalen Unterraum von $\mathcal{P}$ , also eine Hyperebene beschreibt. Da die Gleichung homogen ist, ändert sich ihre Lösungsmenge nicht, wenn man jede Koordinate mit dem gleichen Skalar $r\in K^{*}$ multipliziert, die Hyperebene hängt also nur vom Punkt und dem gewählten projektiven Koordinatensystem ab. Man bezeichnet den Koordinatenvektor $P^{D}=\left[p_{0};p_{1};\ldots p_{n}\right]^{D}$ als Hyperebenenkoordinaten dieser Hyperebene. Jedem Punkt des Raumes wird so durch Dualisierung $P\rightarrow P^{D}$ eineindeutig eine Hyperebene zugeordnet.

Dualität in projektiven Räumen

Die duale Zuordnung von Punkten zu Hyperebenen kann zu einer Dualität im Verband der projektiven Teilräume eines Projektiven Raumes ausgebaut werden. Dabei gelten folgende Zuordnungen:

Begriff	Dualer Begriff
Punkt	Hyperebene
Gesamtraum	Leere Menge als -dimensionaler Teilraum
-dimensionaler Teilraum	-dimensionaler Teilraum
Schnitt $S\cap T$ von zwei Teilräumen	Verbindungsraum $S^{D}\vee T^{D}$ von zwei Teilräumen
Doppelverhältnis von vier kollinearen Punkten	Doppelverhältnis von vier Hyperebenen, die sich in einem -dimensionalen Teilraum schneiden

Die Zuordnung ist auch umgekehrt zu verstehen, da die Dualisierung involutorisch ist: Einer Hyperebene entspricht dual ein Punkt. Während die konkrete Dualisierung vom gewählten Koordinatensystem abhängt, sind allgemeine Sätze davon nicht betroffen.

Das Dualitätsprinzip der projektiven Geometrie beruht auf dem algebraischen Dualraum des endlichdimensionalen Koordinatenvektorraums $K^{{n+1}}$ , siehe dazu den Hauptartikel „Dualraum“. Anwendungsbeispiele in der ebenen Geometrie finden sich in „Dualität (Mathematik)“ im Abschnitt „Dualitätsprinzip der projektiven Geometrie und in Inzidenzstrukturen“.

Dreidimensionale Beispiele

In einem dreidimensionalen Raum $KP^{3}$ ist die Menge der Geraden (eine Gerade entspricht einem 2-dimensionalen Unterraum von K^4 ) zu sich selbst dual. Die konkrete Gerade

$g=\langle e_{0},e_{1}\rangle =\lbrace \left[r,s,0,0\right]:\;(r,s)\in K^{2}\setminus \lbrace 0\rbrace \rbrace$

ist dual zu

$g^{D}=\lbrace \left[x_{0},x_{1},x_{2},x_{3}\right]:(x_{0},x_{1},x_{2},x_{3})\in K^{4}\setminus \lbrace 0\rbrace ,x_{0}=x_{1}=0\rbrace =\langle e_{2},e_{3}\rangle$

Dies ist eine zu windschiefe Gerade! Die Aussage „Die Geraden und $g^{D}$ schneiden einander nicht.“ ist dual zu „Der Verbindungsraum von $g^{D}$ und ist der gesamte dreidimensionale Raum.“ Für zwei beliebige windschiefe Geraden und kann stets eine Punktbasis gewählt werden, bezüglich der $g^{D}=h$ gilt – man wählt zu jeder Geraden zwei linear unabhängige, erzeugende Vektoren und ergänzt diese vier Vektoren durch ihre Summe als Einheitspunkt. Also sind die Aussagen „Zwei Geraden schneiden einander nicht“ und „Zwei Geraden spannen den Raum auf“ zueinander duale Beschreibungen der Eigenschaft „windschief“.

Dagegen sind die Aussagen „ und schneiden sich in einem Punkt“ und „ und spannen eine Ebene auf“ äquivalent aber nicht dual zueinander, da die erste Aussage nicht für beliebige Paare von Geraden gilt und die dazu duale Aussage von anderen Geraden handelt!

Basierend auf einem Artikel in:

Wikipedia.de