Dualität (Mathematik)

Dualität als übergreifendes Prinzip

Dualität als Prinzip nutzt im allgemeinsten Sinne die Betrachtung eines Objektes von einer zweiten, dualen, Seite zum Zwecke des Erkenntnisgewinns. Dualität ist also eine enge Beziehung zwischen mathematischen oder naturwissenschaftlichen Objekten, die Ähnlichkeiten derart aufweisen, dass diese zur (vereinfachten) Lösung von Problemen genutzt werden können. Der Zweck dieses Vorgehens liegt darin, dass sich manche Probleme von der einen Betrachtungsweise aus leichter lösen lassen, andere von der zweiten (dualen) Betrachtungs- oder Herangehensweise. Ein vereinfaches Beispiel ist, dass sich einfache Rechenaufgaben lösen lassen, indem man Finger zur Hilfe nimmt, oder indem man Zahlen und Formeln algebraisch notiert oder auch grafisch, durch Zeichnen.

Dualität ist eines der wichtigsten erkenntnistheoretischen Prinzipien der Mathematik und Naturwissenschaften und nimmt in sehr vielen völlig unterschiedlichen Gebieten eine wichtige Rolle ein, in der Mathematik namentlich etwa in der Geometrie, Algebra und Analysis.

Ähnlich wie im Begriff Dualismus können bei der Dualität in der Mathematik und Naturwissenschaft oft Gegensätze zwischen dualen Objekten im den Betrachtungsfokus rücken, dies ist jedoch nicht zwingend.

Der oben verwendete Begriff der "engen Beziehung" ist mathematisch formal formuliert, eine Abbildung. Dualität ist also eine eins-zu-eins-Abbildung von mathematischen Begriffen, Theoremen oder Strukturen auf andere Begriffe, Theoreme und Strukturen. Oft, aber nicht immer hat die verwendete Abbildung dabei die Form einer Involution (Mathematik), einer selbstinversen Abbildung: Wenn B das Duale von A ist, ist dabei A wieder das Duale von B.

Ein Beispiel für zwei bekannte Gebiete mit einer tiefgreifenden Dualität sind die Mengenlehre und die Logik. Sätze etwa der Aussagenlogik lassen sich auch durch Mengen ausdrücken. Insbesondere entspricht dem logischen "Und" ( $<\wedge >$ ) in der Mengenlehre der Schnitt zweier Mengen ( $\cap$ ) sowie dem logischen "Oder" ( $\vee$ ) die Vereinigung zweier Mengen ( $\cup$ ). Logische Beweise lassen sich also durch solche in der Mengenlehre ersetzen, die in bestimmten Bereichen anschaulicher zugänglich ist.

Dualitäten müssen nicht perfekt sein, nicht immer sind duale Abbildungen vollständig oder die dualen Strukturen im Verhalten zu 100% übertragbar. Auch in der Mathematik gibt es dazu Beispiele. So gilt eine Dualität zwischen Punkten und Geraden nicht in der klassischen (Euklidischen) Geometrie, jedoch in der Projektiven Geometrie.

Im Prinzip ist es ausreichend, wenn trotz Unvollständigkeiten in der Dualität zwischen Strukturen nachgewiesen werden kann, dass diese für eine bestimmte Problemstellung nicht relevant sind. Erkenntnistheoretisch ergibt sich dadurch eine gewisse Verwandtschaft zur Analogie, die jedoch ungleich schwächer ist und naturwissenschaftlich allenfalls als Ideenquelle für weitere Untersuchungen dienen kann, etwa auch zur Untersuchung mathematischer Objekte, ob eine formale Dualität besteht.

Beispiele für Nichtmathematiker

Dualität durch logische Verneinung

Eines der einfachsten Beispiele der Dualität ist Umkehrung, die Inversion, etwa bei Anwendung des indirekten Beweises. Zu jeder Aussage gibt es einfach konstruierbar die logisch inverse Aussage.

Betrachten wir die Aussage "Alle Vögel können fliegen". Diese gilt es auf Wahrheit zu untersuchen. Diese direkt zu beweisen, hieße genau genommen, alle Vögel zu untersuchen, genauer, alle Tiere, die Biologen den Vögeln zuordnen. Der Mensch nimmt in seinem Alltag Unvollständigkeit in Kauf, in dem er diesen Satz (z.B. in jungen Jahren) zunächst "glaubt", wenn er ausreichend viele bestätigende Beispiele sowie kein Gegenbeispiel kennt. Der Fachbegriff hierfür wäre die (unvollständige) Induktion, eine nicht zuverlässige, vor allem streng logisch nicht zulässige Schlußform.

Zunächst wird der betrachtete Satz genauer umformuliert zu "Alle Vogelarten können fliegen", um z.B. Fälle von Verletztheit o.ä auszuschließen. Die logisch umgekehrte (inverse) Aussage hierzu ist: "Nicht alle Vogelarten können fliegen". Diesen kann man wiederum umformulieren zu "Es gibt eine Vogelart, die nicht fliegen kann".

Diese Aussage kann man als dual zu der ersten betrachten. Offensichtlich ist es viel einfacher, diese inverse Aussage zu beweisen, nämlich, indem man schlicht ein einziges Beispiel für einen solchen Vogel findet, der nicht fliegen kann, also ein Pinguin, ein Vogel Strauß oder auch ein Kakapos.

Praktischerweise ergibt die doppelte Verneinung wieder die Ursprungsaussage oder auf unser Beispiel angewandt: Wenn die inverse Aussage wahr ist, muss die Ursprungsaussage falsch sein. Die hier angewandte Methode ist ein sehr einfaches Beispiel zur mathematischen Methode des indirekten Beweises.

Man kann also eine Menge Aussagen als Aussagenraum betrachten und diesen in einen dualen Raum, hier den Raum der gegenteiligen Aussagen transformieren. an den Beispielen ersichtlich, lassen sich manche Fragestellungen eher im dualen Raum lösen, andere im originalen Raum.

Dualität als formale Abbildung

Grundlage der Dualität ist also eine mathematische Abbildung (Funktion)). Mit Hilfe dieser Abbildung kann man zu jedem mathematischen Objekt der jeweils betrachteten Klasse das duale Objekt konstruieren und zur Untersuchung von heranziehen. Dieses Objekt wird dann mit oder ähnlich bezeichnet, um die Abhängigkeit von zum Ausdruck zu bringen. Dazu gibt es ferner dieselbe, eine ähnliche oder eine umgekehrte Konstruktion, die auf angewendet werden kann, man erhält daraus ein mit X''=(X')' bezeichnetes Objekt. Häufig stehen und X'' in einer engen Beziehung, weshalb Informationen über enthalten muss. Man nennt dann das zu duale und X'' das biduale Objekt. In der zugehörigen mathematischen Dualitätstheorie untersucht man dann, wie Eigenschaften von zu Eigenschaften von übersetzt werden können und umgekehrt.

Bei den genannten Abbildungen in einen Dualraum ist es möglich, dass spezielle Fixpunkte entstehen, also Objekte, die zu sich selbst dual sind.

Dualität kann auch als Funktor (Mathematik) gesehen werden, der einem Raum mathematischer Objekte einen Dualraum zuordnet.

Dualität in der Geometrie

Dualität von Polytopen

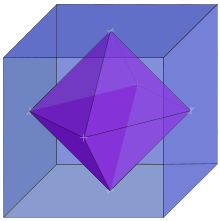
Das duale Polyeder zum Würfel ist das Oktaeder. Die Seitenmitten des einen Körpers bilden die Ecken des anderen.

Zwei Polytope (also Polygone, Polyeder usw.) und heißen kombinatorisch dual, wenn ihre Seitenverbände (die Inklusion ihrer Seiten, also Ecken, Kanten, Flächen usw.) antiisomorph sind. Dazu ein Beispiel: Wählt man die Mittelpunkte der Seitenflächen eines dreidimensionalen konvexen Polyeders als Ecken, und verbindet man zwei „neue“ Ecken, wenn die beiden entsprechenden Seitenflächen von eine gemeinsame Kante haben, d.h. man bildet die konvexe Hülle der „neuen“ Ecken, so erhält man ein duales Polyeder . Die Eckenzahl von ist gleich der Flächenzahl von und umgekehrt, die Kantenanzahlen sind gleich. Solche Dualität nennt man auch dimensionsumkehrend. Dabei gilt: Das Duale des Dualen ist das Original.

Bemerkung

Es gibt auch selbst-duale Körper, bei denen der duale dem Originalkörper ähnlich ist. Ein Beispiel ist das reguläre Tetraeder.

Dies sagt aber nichts darüber aus, ob die Polytope invariant unter den gleichen Symmetrieabbildungen sind. Ein Quadrat und ein beliebiges Viereck sind beispielsweise kombinatorisch dual, da an jeder Ecke zwei Kanten zusammentreffen und jede Kante zwei Ecken hat. In der Regel gehören zu den Symmetrieabbildungen des Vierecks keine Spiegelungen, für das Quadrat hingegen schon.

Zu jedem Polytop gibt es ein spezielles kombinatorisch duales Polytop, die so genannte Polare . Hierzu fasst man das Polytop als abgeschlossene Teilmenge eines euklidischen Vektorraums auf. Die Polare besteht dann aus allen Punkten , die für alle von die Ungleichung $\langle y,x\rangle \leq 1$ erfüllen. Unter der Voraussetzung, dass der geometrische Schwerpunkt von auf der Null liegt, haben und seine Polare dieselbe Symmetriegruppe. Das doppelt-duale Polyeder ist ähnlich zu und gleich diesem, wenn der Nullpunkt in seinem Inneren enthalten ist.

Für Beispiele siehe: Platonischer Körper, Archimedischer Körper

Dualitätsprinzip der projektiven Geometrie und in Inzidenzstrukturen

In der ebenen projektiven Geometrie gilt folgendes Dualitätsprinzip: Vertauscht man in einer wahren Aussage über Punkte und Geraden einer projektiven Ebene die Begriffe „Punkt“ und „Gerade“ und ersetzt man jeweils den Begriff „Verbindungsgerade zweier Punkte“ durch den Begriff „Schnittpunkt zweier Geraden“ und umgekehrt, so erhält man wieder eine wahre Aussage über die duale projektive Geometrie. Für desarguessche projektive Geometrien, also zum Beispiel alle zweidimensionalen projektiven Räume über Körpern, ist die duale projektive Geometrie bis auf Isomorphie identisch zur ursprünglichen Geometrie, also gilt in solchen projektiven Geometrien ein Satz genau dann, wenn der Satz gilt, bei dem die Begriffe „Punkt“ und „Gerade“ vertauscht sind.

Beispiele für Paare dualer Sätze sind der Satz von Desargues und dessen Umkehrung oder der Satz von Pascal und der Satz von Brianchon.

→ Die konkrete Konstruktion der Dualität als Isomorphismus auf einem Projektiven Raum hängt vom gewählten projektiven Koordinatensystem ab und wird daher im Hauptartikel Projektives Koordinatensystem dargestellt.

→ Eine Verallgemeinerung des Dualitätsprinzips in der ebenen projektiven Geometrie ist das Dualitätsprinzip für Inzidenzstrukturen.

Geometrisch dualer Graph

Eine ähnliche Definition kennt auch die Graphentheorie für planare Graphen. Ein zum Graphen G=(V,E) geometrisch dualer Graph G'=(V',E') entsteht, indem in jeder Fläche des Graphen neue Knoten hinzugefügt werden und für jede Kante $e\in E$ eine neue Kante erstellt wird, die die der beiden angrenzenden Flächen verbindet.

Ist der Graph nicht nur planar, sondern auch zusammenhängend, so gilt auch hier, dass die Anzahl der Knoten in der Anzahl der Flächen in entspricht, die Anzahl der Flächen in derjenigen der Knoten in und die Anzahl der Kanten bleibt konstant. Im zusammenhängenden Fall gibt es damit bijektive Abbildungen zwischen den Kantenmengen der beiden Graphen und jeweils den Mengen der Knoten und Flächen. Außerdem gilt, dass G''=G .

Dualraum eines Vektorraums

→ Hauptartikel: Dualraum

Ist ein Vektorraum über einem Körper , so ist der duale Vektorraum oder Dualraum $V^{*}$ der Vektorraum, dessen Elemente die linearen Abbildungen $V\to K$ sind. Ist endlichdimensional, so hat $V^{*}$ dieselbe Dimension wie , und $V^{{**}}$ ist kanonisch isomorph zu .

Im Fall eines Banachraumes besteht der Dualraum X^* aus den stetigen linearen Funktionalen. Ist unendlichdimensional, so ist der Bidualraum $X^{{**}}$ im Allgemeinen nicht kanonisch isomorph zu , es gibt jedoch eine kanonische Einbettung von in den Bidualraum $X^{{**}}$ . Diejenigen Räume, für die diese Einbettung surjektiv ist (und damit ein Isomorphismus), heißen reflexiv. Beispiele sind die Räume L^p für $1<p<\infty$ sowie alle Hilberträume.

Mengenlehre: Komplementbildung

Eine Dualität, die üblicherweise nicht mit diesem Wort bezeichnet wird, ist die Bildung des Komplementes einer Menge: Ist eine Grundmenge gegeben, so ist das Komplement einer Teilmenge $M\subseteq G$ die Menge $M^{\complement }=G\setminus M$ der Elemente von , die nicht in liegen. Das Komplement des Komplementes ist wieder selbst. Die Komplementbildung setzt Vereinigungsmenge und Schnittmenge zueinander in Beziehung: $(M_{1}\cup M_{2})^{\complement }=M_{1}^{\complement }\cap M_{2}^{\complement }$ (siehe de Morgansche Regeln).

Eine Verallgemeinerung dieses Beispiels stellt die Negation in einer beliebigen booleschen Algebra dar.

Nach dem Dualitätsprinzip für Verbände erhält man aus einer beliebigen wahren Aussage über Teilmengen einer Grundmenge wieder eine wahre Aussage, wenn man die Symbole $\cup$ (Vereinigungsmenge) und $\cap$ (Schnittmenge) sowie die Symbole $\emptyset$ (leere Menge) und (Grundmenge) vertauscht.

Siehe auch: Komplement (Mengenlehre), boolesche Algebra

Lagrange-Dualität in der Optimierung

In der mathematischen Optimierung wird die Lagrange-Dualität verwendet. Dabei kann man jedem Optimierungsproblem der Form

${\begin{aligned}{\text{Minimiere }}&f(x)&\\{\text{unter den Nebenbedingungen }}&g_{i}(x)\leq 0&i=1,\dots ,p\\&h_{j}(x)=0&j=1\dots ,q\\&x\in X&\end{aligned}}$ .

ein sogenanntes duales Problem

${\begin{aligned}{\text{maximiere }}&q(\lambda ,\mu )\\{\text{unter den Nebenbedingungen }}&\lambda \geq 0\end{aligned}}$

zuordnen. Dieses hat leichtere Nebenbedingungen als das primale Problem und ist ein konvexes Optimierungsproblem, dafür ist die Zielfunktion meist schwerer zu berechnen. Die Dualität in der Linearen Optimierung ist ein Spezialfall der Lagrange-Dualität. Die Lagrange-Dualität spielt eine wichtige Rolle für Optimalitätskriterien wie zum Beispiel die Karush-Kuhn-Tucker-Bedingungen oder Algorithmen wie Innere-Punkte-Verfahren.

Siehe auch

Der Begriff Dualität ist in der Mathematik weit verbreitet. Die folgende Aufstellung enthält eine Auswahl derartiger Konzepte, die zum Teil sehr fortgeschritten sind.

Dualität im Darstellungssatz für Boolesche Algebren
Duale Form von Differentialformen
Duale Kategorie
Poincaré-Dualität
Pontrjagin-Dualität

Basierend auf einem Artikel in:

Wikipedia.de