

Die konvexe Hülle einer Teilmenge ist die kleinste konvexe Menge, die die Ausgangsmenge enthält. Betrachtet wird dieses Objekt in unterschiedlichen mathematischen Disziplinen wie zum Beispiel in der konvexen Analysis.
Die konvexe Hülle einer Teilmenge
eines reellen oder komplexen Vektorraumes
ist definiert als der Schnitt aller konvexen
Obermengen von .
Sie ist selbst konvex und damit die kleinste konvexe Menge, die
enthält. Die Bildung der konvexen Hülle ist ein Hüllenoperator.
Die konvexe Hülle kann auch beschrieben werden als die Menge aller endlichen Konvexkombinationen:
Der Abschluss
der konvexen Hülle ist der Schnitt aller abgeschlossenen
Halbräume, die
ganz enthalten. Die konvexe Hülle zweier Punkte
ist ihre Verbindungsstrecke:
Die konvexe Hülle endlich vieler Punkte ist ein konvexes Polytop.
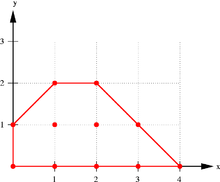
Die Ermittlung der konvexen Hülle von
Punkten im
hat als untere Schranke eine asymptotische Laufzeit von
;
der Beweis erfolgt durch Reduktion auf das Sortieren von
Zahlen. Liegen nur
der
Punkte auf dem Rand der konvexen Hülle, ist die Schranke bei
.
Es bieten sich mehrere Algorithmen zur Berechnung an:

