
Vektorraum
Ein Vektorraum oder linearer Raum ist eine algebraische Struktur, die in vielen Teilgebieten der Mathematik verwendet wird. Vektorräume bilden den zentralen Untersuchungsgegenstand der linearen Algebra. Die Elemente eines Vektorraums heißen Vektoren. Sie können addiert oder mit Skalaren (Zahlen) multipliziert werden, das Ergebnis ist wieder ein Vektor desselben Vektorraums. Entstanden ist der Begriff, indem diese Eigenschaften ausgehend von Vektoren des euklidischen Raumes abstrahiert wurden, sodass sie dann auf abstraktere Objekte wie Funktionen oder Matrizen übertragbar sind.
Die Skalare, mit denen man einen Vektor multiplizieren kann, stammen aus
einem Körper.
Deswegen ist ein Vektorraum immer ein Vektorraum über einem bestimmten
Körper. Sehr oft handelt es sich dabei um den Körper
der reellen Zahlen oder den
Körper
der komplexen Zahlen. Man
spricht dann von einem reellen Vektorraum bzw. einem komplexen
Vektorraum.
Eine Basis eines Vektorraums ist eine Menge von Vektoren, die es erlaubt, jeden Vektor durch eindeutige Koordinaten darzustellen. Die Anzahl der Basisvektoren in einer Basis wird Dimension des Vektorraums genannt. Sie ist unabhängig von der Wahl der Basis und kann auch unendlich sein. Die strukturellen Eigenschaften eines Vektorraums sind eindeutig durch den Körper, über dem er definiert ist, und seine Dimension bestimmt.
Eine Basis ermöglicht es, Rechnungen mit Vektoren über deren Koordinaten statt mit den Vektoren selbst auszuführen, was manche Anwendungen erleichtert.
Definition
Es seien
eine Menge,
ein Körper,
eine innere
zweistellige Verknüpfung, genannt Vektoraddition, und
eine äußere
zweistellige Verknüpfung, genannt Skalarmultiplikation.
Man nennt dann
einen Vektorraum über dem Körper
oder kurz
-Vektorraum,
wenn für alle
und
die folgenden Eigenschaften gelten:
Vektoraddition:
- V1:
(Assoziativgesetz)
- V2: Existenz eines neutralen
Elements
mit
- V3: Existenz eines zu
inversen Elements
mit
- V4:
(Kommutativgesetz)
Skalarmultiplikation:
- S1:
(Distributivgesetz)
- S2:
- S3:
- S4: Neutralität des Einselements
, also
Anmerkungen
- Die Axiome V1, V2 und V3 der Vektoraddition besagen, dass
eine Gruppe bildet, und Axiom V4, dass diese abelsch ist. Ihr neutrales Element
heißt Nullvektor.
- Ein Körper
ist eine abelsche Gruppe
mit neutralem Element (Nullelement)
und einer zweiten inneren zweistelligen Verknüpfung
sodass auch
eine abelsche Gruppe ist und die Distributivgesetze gelten. Wichtige Beispiele für Körper sind die reellen Zahlen
und die komplexen Zahlen
.
- Die Axiome S1 und S2 der Skalarmultiplikation werden ebenfalls als
Distributivgesetze bezeichnet, Axiom S3 auch als Assoziativgesetz.
Dabei ist jedoch zu beachten, dass bei Axiom S2 die Pluszeichen zwei
verschiedene Additionen (links die in
und rechts jene in
) bezeichnen und dass bei Axiom S3 die Skalarmultiplikation assoziativ mit der Multiplikation in
ist.
- Die Axiome S1 und S2 garantieren für die Skalarmultiplikation die Linksverträglichkeit
mit der Vektoraddition und die Rechtsverträglichkeit mit der Körper- und der
Vektoraddition. Axiome S3 und S4 stellen zudem sicher, dass die multiplikative
Gruppe
des Körpers auf
operiert.
- In diesem Artikel werden im Folgenden, wie in der Mathematik üblich,
sowohl die Addition im Körper
als auch die Addition im Vektorraum
mit demselben Zeichen
bezeichnet, obwohl es sich um unterschiedliche Verknüpfungen handelt. Für
wird
geschrieben. Genauso werden sowohl die Multiplikation im Körper als auch die skalare Multiplikation zwischen Körperelement und Vektorraumelement mit
bezeichnet. Bei beiden Multiplikationen ist es auch üblich, den Malpunkt wegzulassen. In der Praxis besteht keine Gefahr, die beiden Additionen oder die beiden Multiplikationen zu verwechseln. Die Verwendung der gleichen Symbole macht die Vektorraumaxiome besonders suggestiv. Zum Beispiel schreibt sich Axiom S1 als
und Axiom S3 als
.
- Mit den beiden Trägermengen
und
sind Vektorräume Beispiele für heterogene Algebren.
- Einen Vektorraum über dem Körper der komplexen bzw. reellen Zahlen bezeichnet man als komplexen bzw. reellen Vektorraum.
Erste Eigenschaften
Für alle
und
gelten folgende Aussagen:
.
.
- Die Gleichung
ist für alle
eindeutig lösbar; die Lösung ist
.
Beispiele
Euklidische Ebene
Ein anschaulicher Vektorraum ist die zweidimensionale Euklidische Ebene
(in rechtwinkligen kartesischen
Koordinatensystemen) mit den Pfeilklassen (Verschiebungen oder
Translationen) als Vektoren und den reellen Zahlen als Skalaren.
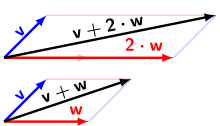
ist die Verschiebung um 2 Einheiten nach rechts und 3 Einheiten nach oben,
die Verschiebung um 3 Einheiten nach rechts und 5 Einheiten nach unten.
Die Summe zweier Verschiebungen ist wieder eine Verschiebung, und zwar diejenige Verschiebung, die man erhält, indem man die beiden Verschiebungen nacheinander ausführt:
, d.h. die Verschiebung um 5 Einheiten nach rechts und 2 Einheiten nach unten.
Der Nullvektor
entspricht der Verschiebung, die alle Punkte an ihrem Platz belässt, d.h.
der identischen Abbildung.
Durch die Streckung der Verschiebung
mit einem Skalar
aus der Menge der reellen Zahlen erhalten wir das Dreifache der Verschiebung:
.
Alles zu diesem Beispiel Gesagte gilt auch in der reellen affinen Ebene.
Koordinatenraum
Ist
ein Körper und
eine natürliche Zahl, so bildet das
-fache
kartesische
Produkt
die Menge aller -Tupel mit Einträgen
in
,
einen Vektorraum über
.
Die Addition und die skalare Multiplikation werden komponentenweise definiert;
für
,
setzt man:
und
Häufig werden die -Tupel
auch als Spaltenvektoren
notiert, das heißt, ihre Einträge werden untereinander geschrieben. Die
Vektorräume
bilden gewissermaßen die Standardbeispiele für endlichdimensionale Vektorräume.
Jeder
-dimensionale
-Vektorraum
ist isomorph zum Vektorraum
.
Mit Hilfe einer Basis kann jedes Element eines Vektorraums eindeutig durch ein
Element des
als Koordinatentupel dargestellt werden.
Funktionenräume
Grundsätzliches und Definition
Ist
ein Körper,
ein
-Vektorraum
und
eine beliebige Menge, so kann auf der Menge
aller Funktionen
eine Addition und eine skalare Multiplikation punktweise definiert werden: Für
und
sind die Funktionen
und
definiert durch
für alle
und
für alle
.
Mit dieser Addition und skalaren Multiplikation ist
ein
-Vektorraum.
Insbesondere gilt dies für
,
wenn also als Zielraum der Körper
selbst gewählt wird. Weitere Beispiele für Vektorräume erhält man als Untervektorräume dieser
Funktionenräume.
In vielen Anwendungen ist ,
der Körper der reellen Zahlen, oder
,
der Körper der komplexen Zahlen, und
ist eine Teilmenge von
,
,
oder
.
Beispiele sind etwa der Vektorraum aller Funktionen von
nach
und die Unterräume
aller stetigen
Funktionen und
aller
-mal
stetig differenzierbaren
Funktionen von
nach
.
Raum der linearen Funktionen
Ein einfaches Beispiel für einen Funktionenraum ist der zweidimensionale Raum der reellen linearen Funktionen, das heißt der Funktionen der Form
mit reellen Zahlen
und
.
Dies sind diejenigen Funktionen, deren Graph eine Gerade ist. Die Menge dieser
Funktionen ist ein Untervektorraum des Raums aller reellen Funktionen, denn die
Summe zweier linearer Funktionen ist wieder linear, und ein Vielfaches einer
linearen Funktion ist auch eine lineare Funktion.
Zum Beispiel ist die Summe der beiden linearen Funktionen
und
mit
,
,
die Funktion
mit
.
Das 3fache der linearen Funktion
ist die lineare Funktion
mit
.
Polynomräume
Die Menge
der Polynome mit Koeffizienten
aus einem Körper
bildet, mit der üblichen Addition und der üblichen Multiplikation mit einem
Körperelement, einen unendlichdimensionalen Vektorraum. Die Menge der Monome
ist eine Basis
dieses Vektorraums. Die Menge der Polynome, deren Grad durch ein
nach oben beschränkt ist, bildet einen Untervektorraum der Dimension
.
Beispielsweise bildet die Menge aller Polynome vom Grad kleiner gleich 4, also
aller Polynome der Form
,
einen 5-dimensionalen Vektorraum mit der Basis .
Bei unendlichen Körpern
kann man die (abstrakten) Polynome mit den zugehörigen Polynomfunktionen
identifizieren. Bei dieser Betrachtungsweise entsprechen die Polynomräume
Unterräumen des Raums aller Funktionen von
nach
.
Zum Beispiel entspricht der Raum aller reellen Polynome vom Grad
dem Raum der linearen Funktionen.
Körpererweiterungen
Ist
ein Oberkörper von
,
so ist
mit seiner Addition und der eingeschränkten Multiplikation
als skalare Multiplikation ein
-Vektorraum.
Die dazu nachzuweisenden Regeln ergeben sich unmittelbar aus den Körperaxiomen
für
.
Diese Beobachtung spielt eine wichtige Rolle in der Körpertheorie.
Beispielsweise ist
auf diese Weise ein zweidimensionaler
-Vektorraum;
eine Basis ist
.
Ebenso ist
ein unendlichdimensionaler
-Vektorraum,
bei dem eine Basis jedoch nicht konkret angegeben werden kann.
Lineare Abbildungen
Lineare Abbildungen sind die Funktionen
zwischen zwei Vektorräumen, die die Struktur des Vektorraums erhalten. Sie sind
die Homomorphismen
zwischen Vektorräumen im Sinne der universellen
Algebra. Eine Funktion
zwischen zwei Vektorräumen
und
über demselben Körper
heißt genau dann linear, wenn für alle
und alle
erfüllt sind. Das heißt,
ist kompatibel mit den Strukturen, die den Vektorraum konstituieren: der
Addition und der Skalarmultiplikation. Zwei Vektorräume heißen isomorph, wenn es eine
lineare Abbildung zwischen ihnen gibt, die bijektiv ist, also eine Umkehrfunktion besitzt.
Diese Umkehrfunktion ist dann automatisch ebenfalls linear. Isomorphe
Vektorräume unterscheiden sich nicht bezüglich ihrer Struktur als Vektorraum.
Basis eines Vektorraums
Für endlich viele
und
bezeichnet man die Summe
als Linearkombination
der Vektoren .
Dabei ist
selbst wieder ein Vektor aus dem Vektorraum
.
Ist
eine Teilmenge von
,
so wird die Menge aller Linearkombinationen von Vektoren aus
die lineare
Hülle von
genannt. Sie ist ein Untervektorraum von
,
und zwar der kleinste Untervektorraum, der
enthält.
Eine Teilmenge
eines Vektorraums
heißt linear abhängig, wenn sich der Nullvektor auf nicht-triviale Weise als
eine Linearkombination von Vektoren
ausdrücken lässt. „Nicht-trivial“ bedeutet, dass mindestens ein Skalar (ein
Koeffizient der Linearkombination) von null verschieden ist. Andernfalls heißt
linear
unabhängig.
Eine Teilmenge
eines Vektorraums
ist eine Basis
von
,
wenn
linear unabhängig ist und die lineare Hülle von
der ganze Vektorraum ist.
Unter Voraussetzung des Auswahlaxioms lässt sich mittels des Lemmas von Zorn beweisen, dass jeder Vektorraum eine Basis hat (er ist frei), wobei diese Aussage im Rahmen von Zermelo Fraenkel äquivalent zum Auswahlaxiom ist. Dies hat weitreichende Konsequenzen für die Struktur eines jeden Vektorraums: Zunächst einmal lässt sich zeigen, dass je zwei Basen eines Vektorraums dieselbe Kardinalität haben, sodass die Kardinalität einer beliebigen Basis eines Vektorraums eine eindeutige Kardinalzahl ist, die man als Dimension des Vektorraums bezeichnet. Zwei Vektorräume über demselben Körper sind nun genau dann isomorph, wenn sie dieselbe Dimension haben, denn aufgrund der Gleichmächtigkeit zweier Basen von zwei Vektorräumen existiert eine Bijektion zwischen ihnen. Diese lässt sich zu einer bijektiven linearen Abbildung, also einem Isomorphismus der beiden Vektorräume, fortsetzen. Ebenso lässt sich zeigen, dass beliebige lineare Abbildungen durch die Bilder von Elementen einer Basis festgelegt sind. Dies ermöglicht die Darstellung jedweder linearer Abbildungen zwischen endlichdimensionalen Vektorräumen als Matrix. Dies lässt sich auf unendlichdimensionale Vektorräume übertragen, wobei jedoch sichergestellt werden muss, dass jede verallgemeinerte „Spalte“ nur endlich viele von Null verschiedene Einträge enthält, damit jeder Basisvektor auf eine Linearkombinationen von Basisvektoren im Zielraum abgebildet wird.
Mittels des Basisbegriffs hat sich das Problem, ein Skelett
in der Kategorie
aller Vektorräume über einem gegebenen Körper zu finden, darauf reduziert, ein
Skelett in der Kategorie der Mengen zu finden, das durch die Klasse der Kardinalzahlen
gegeben ist. Ein jeder -dimensionale
Vektorraum lässt sich auch als die
-fache
direkte Summe des
zugrunde liegenden Körpers auffassen. Die direkten Summen eines Körpers bilden
also ein Skelett der Kategorie der Vektorräume über ihm.
Die Linearfaktoren der Darstellung eines Vektors in den Basisvektoren heißen Koordinaten des Vektors bezüglich der Basis und sind Elemente des zugrunde liegenden Körpers. Erst durch Einführung einer Basis werden jedem Vektor seine Koordinaten bezüglich der gewählten Basis zugeordnet. Dadurch wird das Rechnen erleichtert, insbesondere wenn man statt Vektoren in „abstrakten“ Vektorräumen ihre zugeordneten „anschaulichen“ Koordinatenvektoren verwenden kann.
Untervektorraum
Ein Untervektorraum (auch linearer Unterraum)
ist eine Teilmenge eines Vektorraums, die selbst wieder ein Vektorraum über
demselben Körper ist. Dabei werden die Vektorraumoperationen auf den
Untervektorraum vererbt. Ist
ein Vektorraum über einem Körper
,
so bildet eine Teilmenge
genau dann einen Untervektorraum, wenn die folgenden Bedingungen erfüllt
sind:
- Für alle
gilt
- Für alle
und
gilt
Die Menge
muss also abgeschlossen
bezüglich der Vektoraddition und der Skalarmultiplikation sein. Jeder Vektorraum
enthält zwei triviale Untervektorräume, nämlich zum einen sich selbst, zum
anderen den Nullvektorraum
,
der nur aus dem Nullvektor
besteht. Jeder Unterraum ist Bild
eines anderen Vektorraums unter einer linearen Abbildung in den Raum und Kern einer linearen
Abbildung in einen anderen Vektorraum. Aus einem Vektorraum und einem
Untervektorraum kann man durch Bildung von Äquivalenzklassen
einen weiteren Vektorraum, den Quotientenraum oder Faktorraum, bilden, was
maßgeblich mit der Eigenschaft eines Unterraums zusammenhängt, ein Kern zu sein,
siehe auch Homomorphiesatz.
Verknüpfung von Vektorräumen
Zwei oder mehrere Vektorräume können auf verschiedene Weisen miteinander verknüpft werden, sodass ein neuer Vektorraum entsteht.
Direkte Summe
Die direkte Summe zweier Vektorräume
über dem gleichen Körper besteht aus allen geordneten
Paaren von Vektoren, von denen die erste Komponente aus dem ersten Raum und
die zweite Komponente aus dem zweiten Raum stammt:
Auf dieser Menge von Paaren wird dann die Vektoraddition und die
Skalarmultiplikation komponentenweise definiert, wodurch wiederum ein Vektorraum
entsteht. Die Dimension von
ist dann gleich der Summe der Dimensionen von
und
.
Häufig werden die Elemente von
statt als Paar
auch als Summe
geschrieben. Die direkte Summe kann auch auf die Summe endlich vieler und sogar
unendlich vieler Vektorräume verallgemeinert werden, wobei im letzteren Fall nur
endlich viele Komponenten ungleich dem Nullvektor sein dürfen.
Direktes Produkt
Das direkte Produkt zweier Vektorräume
über dem gleichen Körper besteht, wie die direkte Summe, aus allen geordneten
Paaren von Vektoren der Form
.
Die Vektoraddition und die Skalarmultiplikation werden wieder
komponentenweise definiert und die Dimension von
ist wieder gleich der Summe der Dimensionen von
und
.
Bei dem direkten Produkt unendlich vieler Vektorräume dürfen jedoch auch
unendlich viele Komponenten ungleich dem Nullvektor sein, wodurch es sich in
diesem Fall von der direkten Summe unterscheidet.
Tensorprodukt
Das Tensorprodukt zweier Vektorräume
über dem gleichen Körper wird durch
notiert. Die Elemente des Tensorproduktraums haben dabei die bilineare Darstellung
,
wobei
Skalare sind,
eine Basis von
ist und
eine Basis von
ist. Ist
oder
unendlichdimensional, dürfen hierbei wieder nur endlich viele Summanden ungleich
null sein. Die Dimension von
ist dann gleich dem Produkt der Dimensionen von
und
.
Auch das Tensorprodukt kann auf mehrere Vektorräume verallgemeinert werden.
Vektorräume mit zusätzlicher Struktur
In vielen Anwendungsbereichen in der Mathematik, etwa der Geometrie oder Analysis, ist die Struktur eines Vektorraums nicht hinreichend, etwa erlauben Vektorräume an sich keine Grenzwertprozesse, und man betrachtet daher Vektorräume mit bestimmten zusätzlich auf ihnen definierten Strukturen, die mit der Vektorraumstruktur in gewissen Sinnen kompatibel sind. Beispiele:
- Euklidischer Vektorraum
- Als euklidischer Vektorraum wird (meist) ein reeller Vektorraum mit Skalarprodukt bezeichnet. Er ist ein Spezialfall eines Prähilbertraums (siehe dort für abweichende Nomenklatur).
- Normierter Raum
- Ein normierter Raum ist ein Vektorraum, in dem Vektoren eine Länge (Norm) besitzen. Diese ist eine nichtnegative reelle Zahl und erfüllt die Dreiecksungleichung.
- Prähilbertraum
- Ein Prähilbertraum ist ein reeller oder komplexer Vektorraum, auf dem ein inneres Produkt (Skalarprodukt bzw. positiv definite hermitesche Form) definiert ist. In einem solchen Raum kann man Begriffe wie Länge und Winkel definieren.
- Topologischer Vektorraum
- Ein topologischer
Vektorraum über einem topologischen
Körper
ist ein topologischer Raum
mit einer kompatiblen
-Vektorraumstruktur, d.h., die Vektorraumoperationen
und
sind stetig.
- Unitärer Vektorraum
- Als unitärer Vektorraum wird (meist) ein komplexer Vektorraum mit positiv definiter hermitescher Form ("Skalarprodukt") bezeichnet. Er ist ein Spezialfall des Prähilbertraums.
Bei all diesen Beispielen handelt es sich um topologische Vektorräume. In topologischen Vektorräumen sind die analytischen Konzepte der Konvergenz, der gleichmäßigen Konvergenz und der Vollständigkeit anwendbar. Ein vollständiger normierter Vektorraum heißt Banachraum, ein vollständiger Prähilbertraum heißt Hilbertraum.
Verallgemeinerungen
- Wenn man an Stelle eines Körpers
einen kommutativen Ring zugrunde legt, erhält man einen Modul. Moduln sind eine gemeinsame Verallgemeinerung der Begriffe abelsche Gruppe (für den Ring der ganzen Zahlen) und Vektorraum (für Körper).
- Einige Autoren verzichten in der Definition von Körpern auf das
Kommutativgesetz der Multiplikation und nennen Moduln über Schiefkörpern
ebenfalls Vektorräume. Folgt man dieser Vorgehensweise, so müssen
-Linksvektorräume und
-Rechtsvektorräume unterschieden werden, wenn der Schiefkörper nicht kommutativ ist. [1] Die oben gegebene Definition des Vektorraums ergibt dabei einen
-Linksvektorraum, da die Skalare im Produkt auf der linken Seite stehen.
-Rechtsvektorräume werden analog mit der spiegelbildlich erklärten Skalarmultiplikation definiert. Viele fundamentale Ergebnisse gelten völlig analog auch für Vektorräume über Schiefkörpern, etwa die Existenz einer Basis.
- Wenn man an Stelle eines Körpers
einen Halbkörper zugrunde legt, erhält man einen Halbvektorraum.
- Eine andere Verallgemeinerung von Vektorräumen sind Vektorbündel; sie bestehen aus je einem Vektorraum für jeden Punkt eines topologischen Basisraums.
Anmerkungen
- ↑ Die Situation ist vergleichbar mit der von Links- und Rechts-Moduln über einem (im Allgemeinen) nicht-kommutativen Ring.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 23.10. 2019