Freier Modul

Im mathematischen Teilgebiet der Algebra ist ein freier Modul ein Modul, der eine Basis besitzt. Damit ist der Begriff des freien Moduls eine Verallgemeinerung der Begriffe Vektorraum oder freie abelsche Gruppe.

Definition

Eine Familie $B:=\{b_{i}\mid i\in I\}$ von Elementen eines Moduls (oder allgemeiner eines Linksmoduls) über einem Ring heißt linear unabhängig oder frei, wenn für jede endliche Indexmenge $\textstyle J\subseteq I$ und alle $\textstyle r_{i}\in R$ gilt:

$\sum_{i\in J} r_i \cdot b_i = 0 \;\Rightarrow\; \forall i\in J\colon r_i=0.$

Erzeugen die $\{b_{i}\mid i\in I\}$ zugleich den Modul , so heißt eine Basis (von ) und der Modul heißt der freie -Modul über oder auch einfach frei.

Anmerkungen

Erste Beispiele und Gegenbeispiele

Jeder Ring ist über sich selbst frei. Das heißt $R_{R}$ ist freier Rechtsmodul. Entsprechend ist $_{R}R$ ein freier Linksmodul.
Ist $1<n\in \mathbb{N}$ , so ist der $\mathbb {Z}$ -Modul $\mathbb{Z } /n\mathbb{Z }$ nicht frei. Der $\mathbb {Z}$ -Modul $\Q$ ist torsionsfrei, aber nicht frei (freie Moduln sind immer torsionsfrei).
Ist eine natürliche Zahl, so ist $R^n =\left\{\begin{pmatrix} r_1,\dots, r_n\end{pmatrix}\mid r_1,\dots r_n \in R\right\}$ ein freier Modul. Eine Basis ist die Familie $(e_{i}\mid i\in \{1,\dots ,n\})$ . Dabei ist die -te Komponente von $e_{i}$ gleich , alle anderen Komponenten sind $0$ . Dieses Beispiel ordnet sich folgender Situation unter: Ist eine beliebige Menge, und $(F_{i}|i\in I)$ eine Familie von Moduln, so ist das Koprodukt $\bigoplus _{{i\in I}}F_{i}$ genau dann frei, wenn alle $F_{i}$ frei sind. Insbesondere ist $R^{{(I)}}$ frei.
Das Produkt einer Familie von freien Moduln ist im Allgemeinen nicht frei. So ist beispielsweise $\mathbb{Z } ^{{\mathbb{N} }}$ nicht frei.
Der Polynomring $\textstyle R[X]$ über dem Ring ist ein freier Modul mit Basis $(X^{i}|i\in \mathbb{N} )$ .
Die Menge der positiven rationalen Zahlen $\mathbb{Q} ^{{+}}$ ist bezüglich der Multiplikation eine kommutative Gruppe. Wegen der eindeutigen Primfaktorzerlegung lässt sich jedes $r\in \mathbb{Q} ^{{+}}$ eindeutig schreiben $r=p_{1}^{{z_{1}}}\cdots p_{n}^{{z_{n}}}$ mit Primzahlen $p_{1},\dots ,p_{n}$ . Es ist also $\mathbb{Q} ^{{+}}$ eine freie abelsche Gruppe mit abzählbarer Basis.
Der Ring ist genau dann ein Schiefkörper, wenn jeder Modul über diesem Ring frei ist.

Der Rang eines freien Moduls

Viele der Sätze über Basen von Vektorräumen gelten bei freien Moduln nicht mehr:

Ist $\textstyle V$ ein Vektorraum über dem Körper mit einer Basis von $\textstyle n$ Elementen, so ist jedes System von $\textstyle n$ freien Elementen auch ein Erzeugendensystem, also eine Basis. Über Ringen gilt das im Allgemeinen nicht: So ist beispielsweise im $\mathbb {Z}$ -Modul $\mathbb {Z}$ die Menge $\textstyle \{2\}$ frei, aber keine Basis.
Ist ein Vektorraum, so sind je zwei Basen gleich mächtig. Dies gilt noch bei kommutativen Ringen. Ist also der Ring kommutativ und $R^{n}\cong R^{m}$ , so ist .
Es gilt allgemeiner: Ist $\rho \colon R\rightarrow S$ ein Homomorphismus von Ringen und ist ein IBN-Ring, so auch . Gibt es also beispielsweise von einen Ringhomomorphismus nach einem noetherschen Ring , so ist ein IBN-Ring.

Eigenschaften freier Moduln

Allgemeine Eigenschaften

Ist $(m_{i}|i\in I)$ eine Familie von Elementen aus dem Modul , so gibt es genau einen Homomorphismus $R^{(I)}= \bigoplus_{i \in I}R e_i \rightarrow M$ mit $f(e_{i})=m_{i}$ . Dabei ist $(e_{i}|i\in I)$ eine Basis (im Zweifel die kanonische) von $R^{{(I)}}$ . Erzeugt die Familie $(m_{i}|i\in I)$ den Modul , so ist ein Epimorphismus. Jeder Modul ist also epimorphes Bild eines freien Moduls.
Ist ein freier Modul und $f\colon M\rightarrow F$ ein Epimorphismus, so ist $\operatorname {Kern}(f)$ direkter Summand in . Es gibt ein $g\colon F\rightarrow M$ mit $f\circ g={\mathbf {1}}_{F}$ .
Die Aussage 1. kann allgemeiner und zugleich genauer ausgedrückt werden. Zu jeder Menge gehört der freie Modul ${\mathbf {F}}(X):=R^{{(X)}}$ und die kanonische injektive Abbildung $\Phi (X)\colon X\ni x\mapsto e_{x}\in R^{{(X)}}$ . Ist eine weitere Menge und $\alpha \colon X\rightarrow Y$ eine Abbildung zwischen den Mengen, so gibt es zu der Familie $(e_{{\alpha (x)}}|x\in X)$ genau einen Homomorphismus ${\mathbf {F}}(\alpha )\colon {\mathbf {F}}(X)\rightarrow {\mathbf {F}}(Y)$ , so dass ${\mathbf {F}}(\alpha )\circ \Phi (X)=\Phi (Y)\circ \alpha$ gilt. Das heißt folgendes Diagramm ist kommutativ:
Sind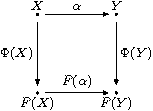 $\alpha \colon X\rightarrow Y\,\beta \colon Y\rightarrow Z$ Abbildungen, so ist ${\mathbf {F}}(\alpha \circ \beta )={\mathbf {F}}(\alpha )\circ {\mathbf {F}}(\beta )$ . In der Sprache der Kategorientheorie lässt sich das so ausdrücken: $\mathbf{F}$ ist ein treuer Funktor von der Kategorie der Mengen in die Kategorie der freien Moduln. $\Phi$ ist ein funktorieller Monomorphismus zwischen dem Identitätsfunktor und dem Funktor $\mathbf{F}$ .
Wie in 3. gehört zu jedem Modul der freie Modul $F(M) = R^{(M)}=\bigoplus_{m \in M}R e_m$ . Dazu gehört der eindeutig bestimmte Epimorphismus $\Psi (M):F(M)\ni e_{m}\mapsto m\in M$ . Für alle $\alpha \colon M\rightarrow N$ ist $\Psi (N)\circ F(\alpha )=\alpha \circ \Psi (N)$ . Es ist $\Psi$ ein funktorieller Epimorphismus zwischen dem Funktor $\mathbf{F}$ und dem Identitätsfunktor.

Freie Moduln über besondere Ringen

Über Hauptidealringen ist jeder Untermodul eines freien Moduls wieder frei.
Über lokalen Ringen sind alle direkte Summanden von freien Moduln (das sind projektive Moduln) frei.

Konstruktion

Zu jeder Menge und jedem Ring gibt es den freien -Linksmodul über . Sein Träger ist die Menge der formalen Linearkombinationen von -Elementen, kodiert etwa als $FS:=\{v\colon S\to R\mid \{s\in S\mid v(s)\neq 0\}{\text{ endlich}}\}$ . Addition und Skalarmultiplikation erfolgen dabei punktweise:

		$\colon$	$FS\times FS\to FS$
	$\cdot$	$\colon$	$R\times FS\to FS$	$(r\cdot v)(s):=r\cdot v(s)$

Die Elemente von sind hierbei keine Elemente von . Wenn eine 1=:e (oder auch nur eine Links-Erzeugende mit $\mathbb{Z } e+Re=R$ ) hat, so dass lassen sie sich aber einbetten mittels

	$\eta _{S}$	$\colon$	$S\to FS$	$\eta _{S}(s):$	$S\to R$
					$t\mapsto {\begin{cases}e&s=t\\0&{\text{sonst.}}\end{cases}}$

Der freie -Rechtsmodul ist der freie $R^{{\text{op}}}$ -Linksmodul, wobei $R^{{\text{op}}}$ den Gegenring von bezeichnet.

Abschwächungen

Das folgende Diagramm setzt die Freiheit eines Moduls über einem kommutativen Ring mit den Eigenschaften projektiv, flach und torsionsfrei in Beziehung:

Moduleigenschaften kommutative Algebra.svg

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de