
Homogene Koordinaten

In der projektiven Geometrie werden homogene Koordinaten verwendet, um Punkte in einem projektiven Raum durch Zahlenwerte darzustellen und damit geometrische Probleme einer rechnerischen Bearbeitung zugänglich zu machen. Im Vergleich zu den normalerweise verwendeten (inhomogenen) Koordinaten, die jeden Punkt eindeutig identifizieren, haben homogene Koordinaten die Eigenschaft, dass sie für einen vorgegebenen Punkt nicht eindeutig bestimmt sind. Der Vorteil homogener Koordinaten liegt in der einheitlichen Darstellung der Elemente eines projektiven Raums, bei der Fernelemente keine Sonderrolle mehr spielen. Zudem lassen sich durch die Verwendung homogener Koordinaten alle Kollineationen, und damit auch Parallelverschiebungen, einheitlich durch lineare Abbildungen und damit durch Matrizen beschreiben. Aus diesem Grund spielen homogene Koordinaten im dreidimensionalen Raum eine wichtige Rolle in der Computergrafik.
Projektive Koordinatensysteme
Homogene Koordinaten

Homogene Koordinaten lassen sich am besten am Beispiel der reellen projektiven Ebene verstehen. Die projektive Gerade und höherdimensionale projektive Räume werden analog mit Koordinaten versehen. Im homogenen Modell der reellen projektiven Ebene entspricht
- ein Punkt der projektiven Ebene einer Ursprungsgerade im dreidimensionalen Raum und
- eine Gerade der projektiven Ebene einer Ursprungsebene im dreidimensionalen Raum.
Ein Punkt liegt dann auf einer Gerade, falls die zum Punkt gehörige
Ursprungsgerade in der zur Gerade gehörenden Ursprungsebene liegt (siehe Bild).
Ein Punkt
der projektiven Ebene kann damit durch einen beliebigen Punkt
der zugehörigen Ursprungsgerade beschrieben werden. Man schreibt dann
und nennt
homogene Koordinaten des Punktes
.
Offensichtlich gilt
für jede Zahl .
Eine Gerade der projektiven Ebene wird dann durch eine (homogene) Ebenengleichung
beschrieben. In diesem Modell überzeugt man sich leicht von den grundlegenden
Inzidenzeigenschaften einer projektiven Ebene:
- Zu je zwei Punkten gibt es genau eine Verbindungsgerade, die beide Punkte enthält.
- Je zwei Geraden besitzen genau einen Schnittpunkt.
Inhomogene Koordinaten
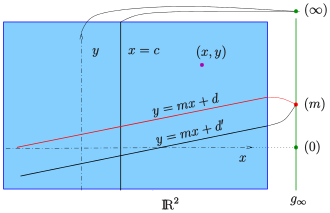
Beim inhomogenen Modell der reellen projektiven Ebene geht man von der Anschauungsebene aus und ergänzt die Punktmenge durch Fernpunkte so, dass sich je zwei Geraden, also auch parallele Geraden, in genau einem Punkt schneiden.
Nach Einführung von kartesischen Koordinaten fügt man jeder Gerade
mit der Steigung
üblicherweise den Fernpunkt
hinzu. Die Geraden
(Parallelen zur y-Achse) erhalten den Fernpunkt
(siehe Bild). Da auch je zwei Fernpunkte durch eine Gerade verbunden sein
müssen, fasst man alle Fernpunkte zur Ferngerade
zusammen. Man prüft leicht nach, dass die neue Inzidenzstruktur (erweiterte
Anschauungsebene) die wesentlichen Eigenschaften einer projektiven Ebene
erfüllt:
- Je zwei Punkte haben genau eine Verbindungsgerade.
- Je zwei Geraden haben genau einen Schnittpunkt.
Isomorphie

Um zu zeigen, dass das homogene und das inhomogene Modell der reellen
projektiven Ebene isomorph sind, wird das inhomogene Modell derart in den
dreidimensionalen Raum eingebettet, dass die Punkte der Anschauungsebene die
Gleichung
erfüllen:
.
Damit wird dem Punkt
des inhomogenen Modells der Punkt
des homogenen Modells zugeordnet. Ein Punkt
wird dabei auf denjenigen Punkt
abgebildet, dessen homogene Koordinaten die Gleichung
erfüllen. Also kann man dem allen inhomogenen Geraden
gemeinsamen Fernpunkt
die allen Ursprungsebenen
gemeinsame Ursprungsgerade
zuordnen (siehe Bild).
Der große Vorteil homogener Koordinaten gegenüber den anschaulicheren inhomogenen Koordinaten liegt in der homogenen Darstellung der Punkte und Geraden. Fernpunkte und Ferngerade spielen formal keine Sonderrolle mehr und alle Kollineationen, einschließlich der Translationen, lassen sich einheitlich durch lineare Abbildungen (Matrizen) beschreiben. Letzteres spielt insbesondere in der Computergrafik eine große Rolle.
Zusammenfassung:
Umkehrung:
, falls
, falls
Zuordnung der Geraden:
Die Einbettung wird in der Literatur nicht einheitlich dargestellt. So können
die homogenen Koordinaten auch mit
bezeichnet sein oder die Ferngerade die Gleichung
erfüllen.
Allgemeine Definition
Jeder Punkt in einem -dimensionalen
projektiven
Raum kann durch
Koordinaten beschrieben werden. Der projektive Raum
über dem Körper
ist definiert als der Faktorraum
des Koordinatenraums
ohne dem Nullvektor
bezüglich der Äquivalenzrelation
.
Die homogenen Koordinaten eines Punkts
des projektiven Raums sind dann
,
wobei
ein beliebiges Element der entsprechenden Äquivalenzklasse
ist. Homogene Koordinaten werden häufig durch
oder
notiert, wobei die Doppelpunkte andeuten sollen, dass die Darstellung nur bis auf Multiplikation mit einer Konstante eindeutig ist.
Projektive Transformationen
Im zweidimensionalen Raum
Im Folgenden werden Beispiele und schließlich alle affinen Abbildungen
zunächst im inhomogenen Modell zu Projektivitäten fortgesetzt und dann im
homogenen Modell durch Matrizen beschrieben. Es ist aber darauf zu achten, dass
die jeweiligen Matrizen (im homogenen Modell) nicht eindeutig bestimmt sind.
Denn nicht nur die Einheitsmatrix ,
sondern jedes vielfache
(Skalierungsmatrix im
)
lässt jede Ursprungsgerade (projektiver Punkt) invariant. Man kann also die
Matrix einer Projektivität mit einer beliebigen Skalierungsmatrix
multiplizieren, ohne dass sich die zugehörige Projektivität ändert.
| a): |
|
| b): |
|
| c): |
Die Fortsetzungen der Affinitäten liefern nur solche Kollineationen, die die Ferngerade als ganzes fest lassen. Die zugehörigen Matrizen im homogenen Modell zeichnen sich dadurch aus, dass sie in den ersten beiden Spalten an der 3. Stelle eine 0 haben. Es treten also noch nicht alle Matrizen auf. Aber es gilt:
- Jede reguläre 3×3-Matrix (Determinante nicht 0) induziert eine
Kollineation der projektiven Ebene, die man Projektivität nennt. Die
Menge der Projektivitäten bilden die Gruppe
(projektive lineare Gruppe).
Z.B.: Die Matrix
induziert eine Projektivität, die im inhomogenen Modell die Ferngerade
mit der y-Achse vertauscht und den Punkt
mit dem Punkt
.
(Die Punkte
sind Fixpunkte.) Sie ist also keine Fortsetzung einer Affinität.
Will man eine beliebige Projektivität im inhomogenen Modell darstellen, so ist dies nur mit gebrochen linearen Ausdrücken möglich. Hier zeigt sich die Stärke des homogenen Modells. Es kommt mit linearen Ausdrücken aus.
Im dreidimensionalen Raum
Homogene Koordinaten können analog zum ebenen Fall auch im 3 dimensionalen projektiven Raum eingeführt werden. Es gibt dann 4 homogene Koordinaten und die Abbildungsmatrizen der Projektivitäten sind 4×4-Matrizen. In der Computergrafik werden nicht nur Transformationen des Raums in homogenen Koordinaten durch 4×4-Matrizen dargestellt sondern auch Projektionen des Raumes auf eine Ebene. Da bei solchen Projektionen die Dimension verkleinert wird (von 3 auf 2) haben die zugehörigen Matrizen die Determinante 0. Hier zwei Beispiele von Projektionsmatrizen:
Die erste Matrix beschreibt die Zentralprojektion vom Augpunkt
aus auf die x-y-Ebene. Die zweite Matrix bewirkt eine
Orthogonalprojektion auf die x-y-Ebene.
| Zentralprojektion: | = | |||
| Orthogonale Projektion: | = |
Anwendungen

Homogene Koordinaten werden innerhalb der Geometrie benutzt um
- Kegelschnitte zu untersuchen (siehe projektive Kegelschnitte),
- Kollineationen von projektiven Geraden, Ebenen und Räume zu untersuchen (projektive lineare Gruppe).
In der Computergrafik werden homogene Koordinaten verwendet um
- Transformationen von Objekten durchzuführen,
- rationale Bézier- und B-Spline-Kurven und -Flächen einzuführen und zu untersuchen.
In der Robotik lassen sich hintereinanderliegende Achsen durch Verkettung ihrer zugehörigen homogenen Matrizen beschreiben. Hierfür wird als Standardverfahren die Denavit-Hartenberg-Transformation angewandt.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 27.10. 2020