
Ebenengleichung
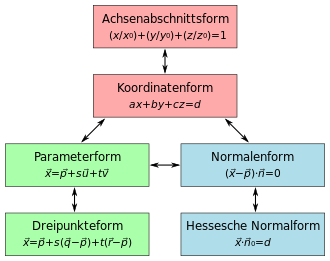
Eine Ebenengleichung ist in der Mathematik eine Gleichung, die eine Ebene im dreidimensionalen Raum beschreibt. Eine Ebene besteht dabei aus denjenigen Punkten in einem kartesischen Koordinatensystem, deren Koordinatenvektoren die Ebenengleichung erfüllen.
Stehen die einzelnen Koordinaten der Ebenenpunkte in einer Gleichungsbeziehung, spricht man von einer Koordinatengleichung, zu denen die Koordinatenform und die Achsenabschnittsform gehören. Stehen die Ortsvektoren der Ebenenpunkte in der Gleichung, handelt es sich um eine Vektorgleichung, zu denen die Parameterform und die Dreipunkteform gehören. Enthält die Gleichung einen Normalenvektor der Ebene, so spricht man von einer Normalengleichung, zu denen die Normalenform und die Hessesche Normalform gehören.
Durch Vektorgleichungen können auch Ebenen in höherdimensionalen Räumen dargestellt werden, während Koordinatengleichungen und Normalengleichungen in diesem Fall Hyperebenen beschreiben.
Koordinatengleichungen
In der analytischen
Geometrie wird jeder Punkt
im dreidimensionalen
Raum mit Hilfe eines kartesischen
Koordinatensystems durch ein Koordinatentupel
identifiziert. Eine Gleichung
mit den Unbekannten
,
und
beschreibt dann eine Menge
von Punkten im Raum, und zwar diejenigen Punkte, deren Koordinaten die Gleichung
erfüllen. Ebenen sind nun dadurch ausgezeichnet, dass es sich bei einer solchen
Gleichung um eine lineare
Gleichung handelt. Zur Notation
von Ebenen werden verschiedene Schreibweisen verwendet. Die vor allem in der Schulmathematik
gebräuchliche Schreibweise
bedeutet, dass die Ebene
aus denjenigen Punkten besteht, deren Koordinaten
die Ebenengleichung
erfüllen. Die in der höheren
Mathematik verwendete Mengenschreibweise lautet entsprechend
.
Für Ebenengleichungen gibt es nun unterschiedliche Darstellungsformen, je nachdem welche Kenngrößen der Ebene vorgeschrieben sind.
Koordinatenform

Bei der Koordinatenform wird eine Ebene durch vier reelle Zahlen ,
,
und
beschrieben. Eine Ebene besteht dann aus denjenigen Punkten, deren Koordinaten
die Gleichung
erfüllen. Hierbei muss mindestens eine der drei Zahlen
ungleich null sein. Die Koordinatenform entspricht der Normalenform (siehe
unten) nach Ausmultiplizieren, wobei
,
und
die Komponenten des (nicht notwendigerweise normierten) Normalenvektors
sind und
gesetzt wird. Der Abstand der Ebene vom Koordinatenursprung ist dann durch
gegeben. Ist der Normalenvektor normiert, dann beträgt der Abstand gerade
.
Achsenabschnittsform

Bei der Achsenabschnittsform wird eine Ebene, die keine Ursprungsebene ist,
durch drei Achsenabschnitte ,
und
beschrieben. Eine Ebene besteht dann aus denjenigen Punkten, deren Koordinaten
die Gleichung
erfüllen. Hierbei sind ,
und
die Schnittpunkte der Ebene mit den drei Koordinatenachsen,
die auch als Spurpunkte bezeichnet werden.
Die Schnittgeraden der Ebene
mit den drei Koordinatenebenen
heißen Spurgeraden und bilden das
Spurdreieck.
Verläuft eine Ebene parallel zu einer oder zwei Koordinatenachsen, dann fällt
der jeweilige Spurpunkt und damit auch der entsprechende Term in der
Achsenabschnittsform weg. Die Achsenabschnittsform kann aus der Koordinatenform
mittels Division durch
errechnet werden.
Vektorgleichungen
Ebenen werden häufig auch mit Hilfe von Vektoren
beschrieben. Eine Ebene besteht dann aus der Menge von Punkten, deren Ortsvektoren die
Ebenengleichung erfüllen. Der Ortsvektor eines Punkts
wird üblicherweise als Spaltenvektor
notiert. Vektorgleichungen sind dann komponentenweise zu verstehen, das heißt jede Komponente des Vektors muss die Gleichung erfüllen. Dabei wird jeder Punkt der Ebene in Abhängigkeit von zwei reellen Parametern beschrieben. Auf diese Weise erhält man eine Parameterdarstellung der Ebene.
Parameterform
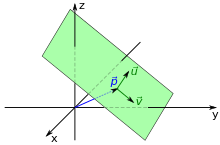
Bei der Parameterform oder Punktrichtungsform wird eine Ebene durch einen Stützvektor
und zwei Richtungsvektoren
und
beschrieben. Eine Ebene besteht dann aus denjenigen Punkten im Raum, deren
Ortsvektoren
die Gleichung
mit
erfüllen. Der Stützvektor ist dabei der Ortsvektor eines beliebigen Punkts in
der Ebene, der auch als Stützpunkt oder Aufpunkt bezeichnet wird. Die beiden
Richtungsvektoren, auch Spannvektoren genannt, müssen in der Ebene liegen und
ungleich dem Nullvektor
sein. Sie dürfen auch nicht kollinear
sein, das heißt
darf kein Vielfaches von
sein und umgekehrt. Die Richtungsvektoren spannen ein affines Koordinatensystem
auf, wobei
die affinen
Koordinaten eines Punkts der Ebene sind. Jedem Wertepaar dieser Parameter
entspricht dann genau ein Punkt der Ebene.
Dreipunkteform

Bei der Dreipunkteform wird eine Ebene durch die Ortsvektoren ,
und
dreier Punkte der Ebene beschrieben. Eine Ebene besteht dann aus denjenigen
Punkten im Raum, deren Ortsvektoren
die Gleichung
mit
erfüllen. Die drei Punkte dürfen dabei nicht alle auf einer Geraden liegen. Auch hier
entspricht jedem Wertepaar der Parameter
genau ein Punkt der Ebene. Aus der Dreipunkteform erhält man die
Punktrichtungsform, indem man einen der drei Punkte als Aufpunkt auswählt und
als Richtungsvektoren die Verbindungsvektoren
von diesem Punkt zu den anderen beiden Punkten wählt. Eine verwandte Darstellung
einer Ebene mit Hilfe dreier Ebenenpunkte verwendet baryzentrische
Koordinaten.
Normalengleichungen
Bei den Normalenformen einer Ebenengleichung werden die Punkte der Ebene durch eine skalare Gleichung mit Hilfe eines Normalenvektors der Ebene charakterisiert. Hierzu wird das Skalarprodukt zweier Vektoren verwendet, das durch
definiert wird. Auf diese Weise erhält man eine implizite Darstellung der Ebene.
Normalenform

Bei der Normalenform wird eine Ebene durch einen Stützvektor
und einen Normalenvektor
beschrieben. Eine Ebene besteht dann aus denjenigen Punkten im Raum, deren
Ortsvektoren
die Gleichung
erfüllen. Das Skalarprodukt zweier Vektoren (ungleich dem Nullvektor) ist
genau dann gleich null, wenn die beiden Vektoren senkrecht
aufeinander stehen. In der Normalenform besteht eine Ebene demnach aus
denjenigen Punkten im Raum, für die der Differenzvektor aus Ortsvektor und
Stützvektor senkrecht zum Normalenvektor der Ebene steht. Aus zwei Spannvektoren
der Ebene
und
lässt sich ein Normalenvektor der Ebene über das Kreuzprodukt
ermitteln.
Hessesche Normalform
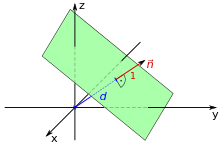
Bei der hesseschen Normalform wird eine Ebene durch einen normierten und
orientierten Normalenvektor
und den Abstand vom Koordinatenursprung
beschrieben. Eine Ebene besteht dann aus denjenigen Punkten im Raum, deren
Ortsvektoren
die Gleichung
erfüllen. Der Normalenvektor muss hierbei die Länge
eins haben und vom Koordinatenursprung in Richtung der Ebene zeigen. Man erhält
die hessesche Normalform aus der Normalenform durch Normierung und Orientierung
des Normalenvektors sowie durch anschließende Wahl von .
Die hessesche Normalform erlaubt eine effiziente Berechnung des Abstands eines beliebigen
Punkts im Raum zu der Ebene, denn das Skalarprodukt
entspricht gerade der Länge der Orthogonalprojektion
eines beliebigen Vektors
auf die Ursprungsgerade
mit Richtungsvektor
.
Verallgemeinerungen
Auch in höherdimensionalen Räumen können Ebenen betrachtet werden. Eine Ebene
ist dann eine lineare
2-Mannigfaltigkeit im -dimensionalen
euklidischen
Raum
.
Die Parameterform und die Dreipunkteform behalten ihre Darstellung, wobei
lediglich mit
-komponentigen
statt dreikomponentigen Vektoren gerechnet wird. Durch die impliziten Formen
wird allerdings in höherdimensionalen Räumen keine Ebene mehr beschrieben,
sondern eine Hyperebene
der Dimension
.
Jede Ebene kann jedoch als Schnitt von
Hyperebenen mit linear
unabhängigen Normalenvektoren dargestellt werden und muss demnach ebenso
viele Koordinatengleichungen gleichzeitig erfüllen.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 16.01. 2022