
Überlagerung (Topologie)
Überlagerungen werden im mathematischen Teilgebiet der Topologie untersucht. Eine Überlagerung eines topologischen Raums besteht aus einem weiteren topologischen Raum, dem Überlagerungsraum, und einer stetigen Abbildung, die aus dem Überlagerungsraum in den Ausgangsraum abbildet und bestimmte Eigenschaften besitzt.
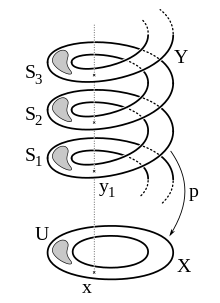
Anschaulich kann man sich eine Überlagerung so vorstellen, dass man den Ausgangsraum auf dem Überlagerungsraum abrollt beziehungsweise den Ausgangsraum mit dem Überlagerungsraum einwickelt.
Definition
Sei
ein topologischer
Raum. Eine Überlagerung von
ist ein topologischer Raum
zusammen mit einer stetigen
surjektiven
Abbildung
so dass es zu jedem Punkt
in
eine Umgebung
gibt, für die das Urbild
unter
aus einer Vereinigung paarweise
disjunkter offener Mengen
besteht, die jeweils mittels p homöomorph
auf
abgebildet werden.
Oft wird der Begriff der Überlagerung sowohl für den Überlagerungsraum
als auch für die Überlagerungsabbildung
benutzt. Für ein
in
heißt
die Faser von
.
Sie besteht aus endlich oder unendlich vielen diskreten Punkten. Im ersten Fall
spricht man von einer endlichen Überlagerung.
Man sagt, die Elemente der Faser liegen über .
Die offenen Mengen
heißen Blätter.
Beispiele
Betrachte den Einheitskreis
in
.
Die reelle Gerade
ist dann eine Überlagerung mit der Überlagerungsabbildung
.
Die Gerade wird also unendlich oft um den Kreis gewickelt. Die Blätter über
einem Intervall des Kreises sind Intervalle auf der Zahlengeraden, die sich mit
Periode
wiederholen. Jede Faser hat unendlich viele Elemente (
).
Die Isomorphie zwischen der Fundamentalgruppe
von
und der additiven Gruppe
über den ganzen Zahlen lässt sich mit Hilfe dieser Überlagerung sehr anschaulich
beweisen.
Die komplexe Ebene ohne den Ursprung, ,
wird von sich selbst überlagert durch die Abbildung
.
Jede Faser hat hier
Elemente.
Ein Beispiel aus der Quantenmechanik
betrifft die Gruppe SO(3)
der Drehungen des dreidimensionalen reellen Raumes .
Zu ihr gehört als „zweifache“ Überlagerung die SU(2), also die Gruppe der
"komplexen Drehungen" des
,
die sogenannte Spinorgruppe. Im Gegensatz zur
SO(3) ist sie einfach
zusammenhängend.
Eigenschaften
Jede Überlagerung ist ein lokaler
Homöomorphismus, das heißt die Einschränkung
der Überlagerungsabbildung
auf eine kleine Umgebung ist ein Homöomorphismus auf eine offene Teilmenge.
Daher besitzen
und
die gleichen lokalen Eigenschaften:
- falls
eine Mannigfaltigkeit ist, so auch jede zusammenhängende Überlagerung von
.
- falls
eine Riemannsche Fläche ist, so ist dies auch jede Überlagerung von
und
ist dann holomorph.
- falls
eine Lie-Gruppe ist, so auch jede Überlagerung von
, und
ist dann ein Lie-Gruppen-Homomorphismus.
- falls
ein CW-Komplex ist, so auch jede Überlagerung von
.
Für jede Zusammenhangskomponente
von
ist die Anzahl der Elemente einer Faser über einem Punkt (und damit die Anzahl
der Blätter über einer Umgebung) stets gleich. Hat jede Faser
Elemente, so spricht man von einer
-fachen
Überlagerung.
Es gilt die Hochhebungseigenschaft: Ist
eine Überlagerung,
ein Weg
in
und
ein Punkt über dem Startpunkt
(d.h.
),
dann gibt es einen eindeutigen Weg
in
über
(d.h.
)
mit Anfangspunkt
.
Wege in
lassen sich also bei Vorgabe eines Startpunkts aus der Faser eindeutig nach
hochheben.
Sind
und
zwei Punkte in
,
die durch einen Weg verbunden sind, so vermittelt der Weg durch die
Hochhebungseigenschaft eine bijektive
Abbildung zwischen den Fasern über
und
.
Universelle Überlagerung
Eine Überlagerung
heißt universelle Überlagerung, falls
einfach zusammenhängend ist.
In der Regel gibt es über einem topologischen Raum
viele verschiedene Überlagerungen. Ist zum Beispiel
Überlagerung von
und
Überlagerung von
,
so ist auch
eine Überlagerung von
.
Der Name „universelle Überlagerung“ kommt daher, dass sie auch
Überlagerung jeder anderen zusammenhängenden Überlagerung von
ist.
Aus der beschriebenen universellen Eigenschaft folgt, dass die universelle Überlagerung bis auf einen Homöomorphismus eindeutig bestimmt ist (zwei universelle Überlagerungen sind nämlich wegen dieser Eigenschaft jeweils die Überlagerung von der anderen, woraus folgt, dass sie homöomorph sein müssen).
Ist
zusammenhängend,
lokal
wegzusammenhängend und semilokal
einfach zusammenhängend, so besitzt
eine universelle Überlagerung. Man kann die universelle Überlagerung
konstruieren, indem man einen Punkt
in
fixiert und zu jedem Punkt
in
die Menge der Homotopieklassen
von Wegen von
nach
betrachtet. Die Topologie erhält man lokal, da
eine Umgebung hat, deren Schleifen global zusammenziehbar sind und auf der daher
die besagten Homotopieklassen überall gleich sein müssen, sodass man das
Kreuzprodukt der Umgebung mit der (diskret topologisierten) Menge der
Homotopieklassen mit der Produkttopologie versehen kann. Unter den genannten
Voraussetzungen ist dieses Konstrukt dann eine universelle Überlagerung.
Die universelle Überlagerung von
wird meist mit
bezeichnet.
Das obige Beispiel
ist eine universelle Überlagerung. Ein anderes Beispiel ist die universelle
Überlagerung des projektiven
Raumes durch die Sphäre
für n > 1.
Die Gruppe der Decktransformationen, reguläre Überlagerungen
Eine Decktransformation einer Überlagerung
ist ein Homöomorphismus
,
der mit der Projektion
verträglich ist, d.h.
.
Die Menge aller Decktransformationen der Überlagerung bildet eine Gruppe mit der Verknüpfung
der Hintereinanderausführung.
Die Decktransformationsgruppe wird mit
bezeichnet.
Aus der Verträglichkeit mit der Projektion folgt, dass jede
Decktransformation einen Punkt aus
wieder auf einen Punkt in der gleichen Faser abbildet. Da die
Decktransformationen darüber hinaus Homöomorphismen, also bijektiv, sind, werden
die Elemente einer Faser permutiert.
Dies definiert eine Gruppenoperation
der Decktransformationsgruppe auf jeder Faser.
Falls
eine Überlagerungsabbildung und
(und damit auch
)
zusammenhängend und lokal wegzusammenhängend ist, so ist die Operation von
auf jeder Faser frei.
Falls die Operation auch transitiv
auf einer Faser ist, so ist sie dies auf allen Fasern. In diesem Fall nennt man
die Überlagerung normal, regulär oder auch galoissch. Dies
ist genau dann der Fall, wenn die charakteristische Untergruppe
ein Normalteiler
ist, was den Namen erklärt.
Zum Beispiel ist jede universelle Überlagerung regulär. Ebenso das Beispiel
.
Hier bestehen die Decktransformationen aus Multiplikationen mit
-ten
Einheitswurzeln,
die Gruppe ist also isomorph zur zyklischen Gruppe der
Ordnung
.
Die Gruppe der Decktransformationen der universellen Überlagerung ist
isomorph zur Fundamentalgruppe des Basisraums; die universelle Überlagerung von
ist ein
-Prinzipalbündel.
Klassifikation
besitze eine universelle Überlagerung
,
und
sei ein Punkt von
.
Die beiden folgenden Konstruktionen liefern eine Äquivalenz von
Kategorien zwischen der Kategorie der Überlagerungen von
und der Kategorie der Mengen mit
-Operation:
- Einer Überlagerung
wird die Faser
zugeordnet.
- Einer Menge
wird das assoziierte Bündel
zugeordnet; es ist ein Faserbündel mit diskreter Faser, also eine Überlagerung.
Zusammenhängenden Überlagerungen entsprechen Mengen mit transitiver
-Operation,
und bis auf Isomorphie sind diese durch Untergruppen von
klassifiziert. Einer zusammenhängenden Überlagerung
entspricht dabei die Untergruppe
.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 25.01. 2021