Homotopie

In der Topologie ist eine Homotopie (von griechisch ὁμός homos ‚gleich‘ und τόπος tópos ‚Ort‘, ‚Platz‘) eine stetige Deformation zwischen zwei Abbildungen von einem topologischen Raum in einen anderen, beispielsweise die Deformation einer Kurve in eine andere Kurve. Eine Anwendung von Homotopie ist die Definition der Homotopiegruppen, welche wichtige Invarianten in der algebraischen Topologie sind.
Der Begriff „Homotopie“ bezeichnet sowohl die Eigenschaft zweier Abbildungen, zueinander homotop (präferiert) zu sein, als auch die Abbildung („stetige Deformation“), die diese Eigenschaft vermittelt.
Definition
Eine Homotopie zwischen zwei stetigen Abbildungen
ist eine stetige Abbildung
mit der Eigenschaft
und
wobei
das Einheitsintervall ist. Der erste Parameter entspricht also dem der
ursprünglichen Abbildungen und der zweite gibt den Grad der Deformation an.
Besonders anschaulich wird die Definition, wenn man sich den zweiten Parameter
als „Zeit“ vorstellt (vgl. Bild).
Man sagt,
sei homotop zu
und schreibt
.
Homotopie ist eine Äquivalenzrelation
auf der Menge der stetigen Abbildungen
,
die zugehörigen Äquivalenzklassen heißen Homotopieklassen, die Menge
dieser Klassen wird häufig mit
bezeichnet.
Eine stetige Abbildung
heißt nullhomotop, wenn sie homotop zu einer konstanten Abbildung ist.
Beispiel
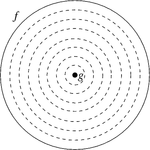
Sei
der Einheitskreis in der Ebene und
die ganze Ebene. Die Abbildung
sei die Einbettung von
in
,
und
sei die Abbildung, die ganz
auf den Ursprung abbildet, also
.
Dann sind
und
zueinander homotop. Denn
mit
ist stetig und erfüllt
und
.
Relative Homotopie
Ist
eine Teilmenge von
,
und stimmen zwei stetige Abbildungen
auf
überein, so heißen
und
homotop relativ zu
,
wenn es eine Homotopie
gibt, für die
für jedes
unabhängig von
ist.
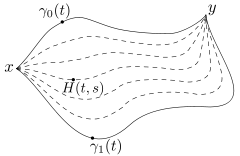
Ein wichtiger Spezialfall ist die Homotopie von Wegen relativ der Endpunkte:
Ein Weg ist eine stetige Abbildung ;
dabei ist
das Einheitsintervall. Zwei Wege heißen homotop relativ der Endpunkte,
wenn sie homotop relativ
sind, d.h. wenn die Homotopie die Anfangs- und Endpunkte festhält. (Sonst
wären Wege in der gleichen Wegzusammenhangskomponente
immer homotop.) Sind also
und
zwei Wege in
mit
und
,
so ist eine Homotopie relativ der Endpunkte zwischen ihnen eine stetige
Abbildung
mit ,
,
und
.
Ein Weg heißt nullhomotop genau dann, wenn er homotop zum konstanten Weg
ist.
Der andere häufig auftretende Fall ist die Homotopie von Abbildungen zwischen
punktierten
Räumen. Sind
und
punktierte Räume, so sind zwei stetige Abbildungen
homotop als Abbildungen von punktierten Räumen, wenn sie relativ
homotop sind.
Beispiel: Die Fundamentalgruppe
Die Menge der Homotopieklassen von Abbildungen punktierter Räume von
nach
ist die Fundamentalgruppe
von
zum Basispunkt
.
Ist zum Beispiel
ein Kreis mit einem beliebigen ausgewählten Punkt
,
dann ist der Weg, der durch einmaliges Umrunden des Kreises beschrieben wird,
nicht homotop zum Weg, den man durch Stillstehen am Ausgangspunkt
erhält.
Homotopieäquivalenz
Seien
und
zwei topologische Räume und sind
und
stetige Abbildungen. Dann sind die Verknüpfungen
und
jeweils stetige Abbildungen von
bzw.
auf sich selbst, und man kann versuchen, diese zur Identität auf X bzw. Y zu
homotopieren.
Falls es solche
und
gibt, dass
homotop zu
und
homotop zu
ist, so nennt man
und
homotopieäquivalent oder vom gleichen Homotopietyp. Die
Abbildungen
und
heißen dann Homotopieäquivalenzen.
Homotopieäquivalente Räume haben die meisten topologischen Eigenschaften
gemeinsam. Falls
und
homotopieäquivalent sind, so gilt
- falls
wegzusammenhängend, so auch
.
- falls
und
wegzusammenhängend, so sind die Fundamentalgruppen und die höheren Homotopiegruppen isomorph.
- die Homologie-
und Kohomologiegruppen von
und
sind gleich.
und
sind Deformationsretrakte eines topologischen Raums
.
Isotopie
Definition
Wenn zwei gegebene homotope Abbildungen
und
zu einer bestimmten Regularitätsklasse
gehören oder andere zusätzliche Eigenschaften besitzen, kann man sich fragen, ob
die beiden innerhalb dieser Klasse durch einen Weg miteinander verbunden werden
können. Dies führt zum Konzept der Isotopie. Eine Isotopie ist eine
Homotopie
wie oben, wobei alle Zwischenabbildungen
(für festes t) ebenfalls die geforderten Zusatzeigenschaften besitzen
sollen. Die zugehörigen Äquivalenzklassen heißen Isotopieklassen.
Beispiele
Zwei Homöomorphismen
sind also isotop, wenn eine Homotopie existiert, so dass alle
Homöomorphismen sind. Zwei Diffeomorphismen
sind isotop, wenn alle
selbst Diffeomorphismen sind. (Man bezeichnet sie dann auch als
diffeotop.) Zwei Einbettungen
sind isotop, wenn alle
Einbettungen sind.
Unterschied zur Homotopie
Zu verlangen, dass zwei Abbildungen isotop sind, kann tatsächlich eine
stärkere Anforderung sein, als zu verlangen, dass sie homotop sind. Zum Beispiel
ist der Homöomorphismus der Einheitskreisscheibe
in ,
der durch
definiert ist, dasselbe wie eine 180-Grad-Drehung um den Nullpunkt, darum sind
die Identitätsabbildung und
isotop, denn sie können durch Drehungen miteinander verbunden werden. Im
Gegensatz dazu ist die Abbildung auf dem Intervall
in
,
definiert durch
nicht isotop zur Identität. Das liegt daran, dass jede Homotopie der
beiden Abbildungen zu einem bestimmten Zeitpunkt die beiden Endpunkte
miteinander vertauschen muss; zu diesem Zeitpunkt werden sie auf denselben Punkt
abgebildet und die entsprechende Abbildung ist kein Homöomorphismus. Hingegen
ist
homotop zur Identität, zum Beispiel durch die Homotopie
,
gegeben durch
.
Anwendungen
In der Geometrischen Topologie werden Isotopien benutzt, um Äquivalenzrelationen herzustellen.
Zum Beispiel in der Knotentheorie
– wann sind zwei Knoten
und
als gleich zu betrachten? Die intuitive Idee, den einen Knoten in den anderen zu
deformieren, führt dazu, dass man einen Weg von Homöomorphismen verlangt: Eine
Isotopie, die mit der Identität des dreidimensionalen
Raumes beginnt und bei einem Homöomorphismus h endet, so dass
h den Knoten
in den Knoten
überführt. Eine solche Isotopie des umgebenden Raumes wird ambiente
Isotopie
oder Umgebungsisotopie genannt.
Eine andere wichtige Anwendung ist die Definition der Abbildungsklassengruppe Mod(M) einer Mannigfaltigkeit M. Man betrachtet Diffeomorphismen von M „bis auf Isotopie“, das heißt, dass Mod(M) die (diskrete) Gruppe der Diffeomorphismen von M ist, modulo der Gruppe der Diffeomorphismen, die isotop zur Identität sind.
Homotopie kann in der numerischen Mathematik für eine robuste Initialisierung zur Lösung von differential-algebraischen Gleichungen eingesetzt werden (siehe Homotopieverfahren).
Kettenhomotopie
Zwei Kettenhomomorphismen
zwischen Kettenkomplexen
und
heißen kettenhomotop, wenn es einen Homomorphismus
mit
gibt.
Wenn
homotope Abbildungen zwischen topologischen Räumen sind, dann sind die
induzierten Abbildungen der singulären
Kettenkomplexe
kettenhomotop.
Punktierte Homotopie
Zwei punktierte Abbildungen
heißen homotop, wenn es eine stetige Abbildung
mit
und
für alle
für alle
gibt. Die Menge der Homotopieklassen punktierter Abbildungen wird mit
bezeichnet.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 02.01. 2022