
Numerische Mathematik
Die numerische Mathematik, auch kurz Numerik genannt, beschäftigt sich als Teilgebiet der Mathematik mit der Konstruktion und Analyse von Algorithmen für kontinuierliche mathematische Probleme. Hauptanwendung ist dabei die näherungsweise Berechnung von Lösungen durch Approximationsalgorithmen mit Hilfe von Computern.
Je nach persönlicher Auffassung ist die numerische Lösung von Differenzialgleichungen eines der wichtigsten Teilgebiete der Numerik. Diese Differenzialgleichungen beschreiben viele Bereiche unserer Umwelt wie technische, wirtschaftliche, biologische oder organisatorische Vorgänge. Für die numerische Lösung bieten sich einfache aber auch aufwendigere Verfahren an.
Ein Praxisbeispiel der Numerik mit einer einfachen diskreten Lösung einer nichtlinearen Differenzialgleichung erläutert die Grundlagen und zeigt den geringen mathematischen Aufwand.
Überblick
Interesse an solchen Algorithmen besteht meist aus einem der folgenden Gründe:
- Es gibt zu dem Problem keine explizite Lösungsdarstellung (so zum Beispiel bei den Navier-Stokes-Gleichungen oder dem Dreikörperproblem) oder
- die Lösungsdarstellung existiert, ist jedoch nicht geeignet, die Lösung schnell zu berechnen, oder liegt in einer Form vor, in der Rechenfehler sich stark bemerkbar machen (zum Beispiel bei vielen Potenzreihen).
Unterschieden werden zwei Typen von Verfahren: Einmal direkte, die nach endlich vielen exakten Rechenschritten die exakte Lösung eines Problems liefern, und auf der anderen Seite Näherungsverfahren, die nur Approximationen liefern. Ein direktes Verfahren ist beispielsweise das gaußsche Eliminationsverfahren, welches die Lösung eines linearen Gleichungssystems liefert. Näherungsverfahren sind unter anderem Quadraturformeln, die den Wert eines Integrals näherungsweise berechnen, oder auch das Newton-Verfahren, das iterativ bessere Approximationen an eine Nullstelle einer Funktion liefert.
Da in Anwendungen die Lösungen nur auf endliche Genauigkeit benötigt werden, kann ein iteratives Verfahren auch bei der Existenz eines direkten Verfahrens sinnvoller sein, wenn es in kürzerer Zeit eine hinreichende Genauigkeit liefert.
Unterschiedliche Verfahren werden nach Laufzeit, Stabilität und Robustheit verglichen. Gelegentlich existieren jedoch auch (abweichend von rein numerischen Verfahren) seminumerische Verfahren, die zur Lösung bestimmter Problemklassen besser geeignet sind als unspezialisierte numerische Lösungen.
Geschichte
Der Wunsch, mathematische Gleichungen zahlenmäßig (auch näherungsweise) lösen
zu können, besteht seit der Antike.
Die alten Griechen kannten bereits Probleme, die sie nur näherungsweise lösen
konnten, wie die Berechnung von Flächen (Integralrechnung)
oder der Kreiszahl .
In diesem Sinne kann Archimedes,
der für beide Probleme Algorithmen lieferte, als der erste bedeutende Numeriker
bezeichnet werden.
Die Namen klassischer Verfahren zeigen deutlich, dass der algorithmische und approximative Zugang zu mathematischen Problemen immer wichtig war, um rein theoretische Aussagen fruchtbar nutzen zu können. Konzepte wie Konvergenzgeschwindigkeit oder Stabilität waren auch beim Rechnen per Hand sehr wichtig. So lässt beispielsweise eine hohe Konvergenzgeschwindigkeit darauf hoffen, schnell mit der Berechnung fertig zu werden. Und schon Gauß bemerkte, dass sich seine Rechenfehler beim gaußschen Eliminationsverfahren manchmal desaströs auf die Lösung auswirkten und sie so komplett unbrauchbar machten. Er zog deswegen das Gauß-Seidel-Verfahren vor, bei dem man Fehler durch das Ausführen eines weiteren Iterationsschrittes leicht ausgleichen konnte.
Um das monotone Durchführen von Algorithmen zu erleichtern, wurden im 19. Jahrhundert mechanische Rechenmaschinen entwickelt, und schließlich in den 1930er-Jahren der erste Computer von Konrad Zuse. Der Zweite Weltkrieg beschleunigte die Entwicklung dramatisch und insbesondere John von Neumann trieb im Rahmen des Manhattan Projects sowohl mathematisch als auch technisch die Numerik voran. Die Zeit des Kalten Krieges war vor allem von militärischen Anwendungen wie Wiedereintrittsproblemen geprägt, doch die Steigerung der Rechnerleistung seit den 1980er-Jahren hat zivile Anwendungen in den Vordergrund treten lassen. Ferner hat sich der Bedarf nach schnellen Algorithmen mit dem Geschwindigkeitszuwachs entsprechend verstärkt. Für viele Probleme hat die Forschung dies leisten können, und so hat sich die Geschwindigkeit der Algorithmen seit Mitte der 1980er-Jahre um etwa dieselbe Größenordnung verbessert wie die CPU-Leistungen. Heutzutage sind numerische Verfahren, zum Beispiel die Finite-Elemente-Methode, in jedem technischen oder wissenschaftlichen Bereich präsent und Alltagswerkzeug.
Fehleranalyse
Ein Aspekt bei der Analyse der Algorithmen in der Numerik ist die Fehleranalyse. Bei einer numerischen Berechnung kommen verschiedene Typen von Fehlern zum Tragen: Beim Rechnen mit Gleitkommazahlen treten unvermeidlich Rundungsfehler auf. Diese Fehler lassen sich zwar zum Beispiel durch eine Erhöhung der Stellenzahl verkleinern, ganz beseitigen kann man sie aber nicht, da jeder Computer prinzipiell nur mit endlich vielen Stellen rechnen kann.
Wie das Problem auf Störungen in den Anfangsdaten reagiert, wird mit der Kondition gemessen. Hat ein Problem eine große Kondition, so hängt die Lösung des Problems empfindlich von den Anfangsdaten ab, was eine numerische Lösung erschwert, insbesondere da Rundungsfehler als Störung der Anfangsdaten aufgefasst werden können.
Das numerische Verfahren ersetzt ferner das kontinuierliche mathematische Problem durch ein diskretes, also endliches Problem. Dabei tritt bereits der sogenannte Diskretisierungsfehler auf, der im Rahmen der Konsistenzanalyse abgeschätzt und bewertet wird. Dies ist notwendig, da ein numerisches Verfahren im Regelfall nicht die exakte Lösung liefert.
Wie sich solche Fehler beim Weiterrechnen vergrößern, wird mit Hilfe der Stabilitätsanalyse bewertet.
Konsistenz und Stabilität des Algorithmus führen im Regelfall zu Konvergenz (siehe dazu: Grenzwert (Funktion)).
Numerische Verfahren
Für viele mathematische Probleme, wie zum Beispiel die Optimierung oder das Lösen von partiellen Differentialgleichungen, existieren eine Vielzahl numerischer Verfahren und Algorithmen.
Grundlagen einfacher Berechnungsmethoden zur numerischen Lösung gewöhnlicher Differenzialgleichungen
Die Lösung von Differenzialgleichungen (Abkürzung DGL) höherer Ordnung, die z.B. dynamische Vorgänge beschreiben, sind mit steigender Ordnung nur mit großem Aufwand lösbar. Die Lösung entspricht einer Funktion mit kontinuierlichem Verlauf.
Wird der Differentialquotient einer DGL durch einen Differenzenquotienten
ersetzt, entsteht eine Differenzengleichung.
Die Lösung der abhängigen Variable des ursprünglichen kontinuierlichen Verlaufs
ändert sich in eine rekursive diskrete
Folge von nummerierten Folgegliedern
.
Neben dem numerischen Verfahren mit Differenzengleichungen (Einschrittverfahren) stehen auch mehrere andere Verfahren zur besseren Approximation an den analytischen Verlauf einer Funktion zur Verfügung. Dazu gehören z.B. das Trapezflächenverfahrens (Heun-Verfahren), Runge-Kutta-Verfahren, das Mehrschrittverfahren (Adams-Bashforth-Verfahren) und andere Verfahren.
Grund der aufwendigeren Approximationsverfahren durch Verwendung komplizierter diskreter Gleichungen ist die erzielbare höhere Genauigkeit und damit Reduzierung der Folgeglieder.
Euler-Streckenzug-Verfahren
Der Mathematiker Leonhard Euler hat bereits im Jahr 1768 eine Methode als einfaches Einschritt-Streckenzugverfahren zur numerischen Lösung von Anfangswertproblemen bei DGL gewöhnlichen Differenzialgleichungen veröffentlicht. Als Beispiel für den Algorithmus des expliziten Eulerverfahrens gilt die Rechenvorschrift:
Eine Differenzengleichung nach "Euler-Vorwärts" entsteht, wenn an Stelle der
Funktion
der oben dargestellten Berechnungsvorschrift die rechte Seite einer DGL
(explizite Darstellung) eingesetzt wird. Die Methode „Euler-Vorwärts“ und die im
nachfolgenden Abschnitt dargestellte Methode der Differenzengleichung nach dem
„Vorwärts-Differenzenquotient“ sind identisch. Hier ist
die unabhängige diskrete Variable.
Anmerkung:
Einfaches Differenzenverfahren
Das Differenzenverfahren erlaubt mit Hilfe von Differenzenquotienten eine DGL unmittelbar in Differenzengleichungen zu überführen und damit DGL-en zu lösen bzw. das Verhalten von dynamischen Systemen zu simulieren.
Die einfachste Form der Differenzengleichung bezieht sich auf den Vorwärts-
oder den Rückwärts-Differenzenquotienten, die je nach Anwendung verschiedene
Vorteile haben, z.B. bei Differenzengleichungen höherer Ordnung (bei DGL
mit konjugiert komplexen Polen) auch beide Arten verwendet werden können. Durch
Einsetzen des Differenzenquotienten entsprechender Ordnung in die DGL entsteht
automatisch das rekursive Verhalten der Differenzengleichung, bei der sich je
nach Ordnung
jedes aktuelle Folgeglied
sich auf ein oder mehrere zurückliegende Folgeglieder bezieht.
Eine Differenzengleichung ist eine numerisch lösbare rekursive
Berechnungsvorschrift für eine diskret
definierte Folge
von fortlaufend nummerierten Folgegliedern bzw. Stützstellen
im Abstand eines meist konstanten Intervalls
oder bei zeitabhängigen Systemen
.
Die Folgeglieder
werden im Abstand
zugeordnet. Die Größe
bedeutet die fortlaufende Indizierung der Folgeglieder. Die Parameter der
Eingangs- und Ausgangsgrößen, die Indizierung k und die Schrittweite
lassen sich mit jeder Programmierungssprache berechnen und vorzugsweise
tabellarisch darstellen.
Numerische Genauigkeit des Differenzenverfahrens
Mit kleiner werdender Schrittweite
steigt linear die Genauigkeit der berechneten Folgeglieder
und damit die Zahl der Folgeglieder. Zur Erzielung einer großen Genauigkeit der
Folgeglieder
kann die Zahl der Folgeglieder nicht beliebig hoch betrieben werden, weil sich
je nach Rechengenauigkeit des Computers unvermeidbare Rundungsfehler zu jedem
Folgeglied aufaddieren können.
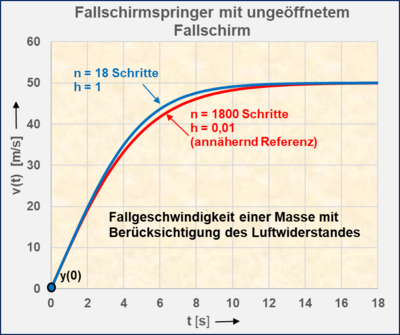
Berechnungsbeispiel für einen Fallschirmspringer bei ungeöffnetem Fallschirm
Die nichtlineare Differenzialgleichung für den senkrechten Fall mit Luftwiderstand lautet:
Daten:
| Reibungskoeffizient: | Masse: | Erdbeschleunigung: | Schrittweite: |
| c = 0,32 kg/m | m = 80 kg | g = 10 m/s² | 1 s und 0,01 s |
Gesucht: Differenzengleichung, Geschwindigkeit
der Masse
.
Differenzengleichung (Vorwärtsdifferenzenquotient):
Anfangswert:
Entwicklung der Folgeglieder der Differenzengleichung bei einer
Schrittweite von
[s]:
-
k Zeit
[s]Fallgeschwindigkeit 0 0 (Anfangswert)
1 1 = 10
2 2 3 3 18 18
Die Ergebnisse der Folgegleichungen ergeben Stützstellen mit asymptotischem
Verlauf. Die Fallgeschwindigkeit nimmt ab
nicht mehr zu.
Die Fallstrecke nach der Fallzeit 13 s beträgt etwa 478 m (mit h = 0,01 s gerechnet).
Diskretes Systemverhalten zusammenhängender dynamische Systeme
- In technischen Bereichen können mehrere dynamische Systeme hintereinander wirken und mehrere Systemeingänge und -Ausgänge aufweisen.
- Bei entkoppelten Mehrfachsystemen können bei hintereinander liegenden Systemen die nummerierten Folgegliedern addiert werden. Haben alle Signaleingänge eines Systems den Wert Null, wird die gespeicherte Energie des Systems mit allen Ausgängen gegen Null abklingen.
- Weist eine DGL 2. Ordnung konjugiert komplexe Pole auf (Schwingungssystem), kann sie nicht in 2 unabhängige Systeme 1. Ordnung überführt werden. Nach der Zustandsraumdarstellung kann sie über die Regelungsnormalform in 2 verkoppelte DGL-en 1. Ordnung überführt werden. Sie werden in zwei Zustandsgleichungen zusammengefasst:
-
und
.
- Ausgehend von einer DGL höherer Ordnung erzeugt man über Zustandsgrößen ein äquivalentes Differenzialgleichungssystem.
- Bei zusammenwirkenden dynamischen Systemen können auch die linearen Wertefolgen mit den Wertefolgen nichtlinearer Systeme addiert werden, d.h. Systeme, die nicht mit DGL-en beschrieben werden können (z.B. Totzeit, Nichtlinearität als Tabelle).
Ausführliche Behandlung des Differenzenverfahrens:
Siehe
Differenzengleichung
(Differenzenverfahren)
Aufstellung der Differenzenquotienten:
Siehe
Differenzenquotient
Literatur
- Wolfgang Dahmen, Arnold Reusken: Numerik für Ingenieure und Naturwissenschaftler. Springer, Berlin u. a. 2006, ISBN 3-540-25544-3.
- Peter Deuflhard, Andreas Hohmann: Numerische Mathematik. Band 1: Eine algorithmisch orientierte Einführung. 3., überarbeitete und erweiterte Auflage. de Gruyter, Berlin u. a. 2002, ISBN 3-11-017182-1.
- Martin Hanke-Bourgeois: Grundlagen der Numerischen Mathematik und des wissenschaftlichen Rechnens. Teubner, Stuttgart u. a, 2002, ISBN 3-519-00356-2.
- Martin Hermann: Numerische Mathematik. Band 1: Algebraische Probleme. 4., überarbeitete und erweiterte Auflage. Walter de Gruyter Verlag Berlin, Boston, 2020, ISBN 978-3-11-065665-7.
- Martin Hermann: Numerische Mathematik. Band 2: Analytische Probleme. 4., überarbeitete und erweiterte Auflage. Walter de Gruyter Verlag Berlin, Boston, 2020, ISBN 978-3-11-065765-4.
- Thomas Huckle, Stefan Schneider: Numerik für Informatiker. Springer, Berlin u. a. 2002, ISBN 3-540-42387-7.
- Hans R. Schwarz, Norbert Köckler: Numerische Mathematik. 8. Auflage. Teubner, Stuttgart 2011, ISBN 978-3-8348-1551-4.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 08.12. 2025