Newtonverfahren
Das Newtonverfahren, auch Newton-Raphson-Verfahren (benannt
nach Sir Isaac
Newton 1669 und Joseph
Raphson 1690), ist in der Mathematik
ein häufig verwendeter Approximationsalgorithmus
zur numerischen
Lösung von nichtlinearen
Gleichungen und Gleichungssystemen. Im Falle einer Gleichung mit einer
Variablen lassen sich zu einer gegebenen stetig
differenzierbaren
Funktion
Näherungswerte zu Lösungen der Gleichung
,
d.h. Näherungen der Nullstellen
dieser Funktion finden. Die grundlegende Idee dieses Verfahrens ist, die
Funktion in einem Ausgangspunkt zu linearisieren, d.h. ihre Tangente zu bestimmen, und die
Nullstelle der Tangente als verbesserte Näherung der Nullstelle der Funktion zu
verwenden. Die erhaltene Näherung dient als Ausgangspunkt für einen weiteren
Verbesserungsschritt. Diese Iteration
erfolgt, bis die Änderung in der Näherungslösung eine festgesetzte Schranke
unterschritten hat. Das Iterationsverfahren konvergiert im günstigsten Fall
asymptotisch mit quadratischer Konvergenzordnung,
die Zahl der korrekten Dezimalstellen verdoppelt sich dann in jedem Schritt.
Formal ausgedrückt, wird ausgehend von einem Startwert
die Iteration
wiederholt, bis eine hinreichende Genauigkeit erzielt wird.
Newtonverfahren für reelle Funktionen einer Veränderlichen
Historisches über das Newton-Verfahren
Isaac Newton verfasste im Zeitraum 1664 bis 1671 die Arbeit „Methodus
fluxionum et serierum infinitarum“ (latein. für: Von der Methode der
Fluxionen und unendlichen Folgen). Darin erklärt er einen neuen Algorithmus
zum Lösen einer polynomialen Gleichung am Beispiel .
Dazu kann man leicht den Punkt
als erste Näherung raten. Newton machte den Ansatz
mit einem als „klein“ angenommenen
und setzte diesen in die Gleichung ein:
Nach den binomischen Formeln gilt
-
.
Da
„klein“ sein soll, können die Terme höherer Ordnung gegenüber den linearen und
konstanten vernachlässigt werden, womit
bzw.
übrig bleibt. Wir können nun dieses Vorgehen wiederholen und
ansetzen, in die zweite Gleichung einsetzen, höhere Terme weglassen und
erhalten.
Joseph Raphson beschrieb 1690 in der Arbeit „Analysis Aequationum universalis“ diesen Rechenprozess formal und illustrierte den Formalismus an der allgemeinen Gleichung dritten Grades, wobei er die nachfolgende Iterationsvorschrift fand.
Die abstrakte Form des Verfahrens mit Benutzung der Ableitung
stammt von Thomas
Simpson.
Konstruktion am Graphen
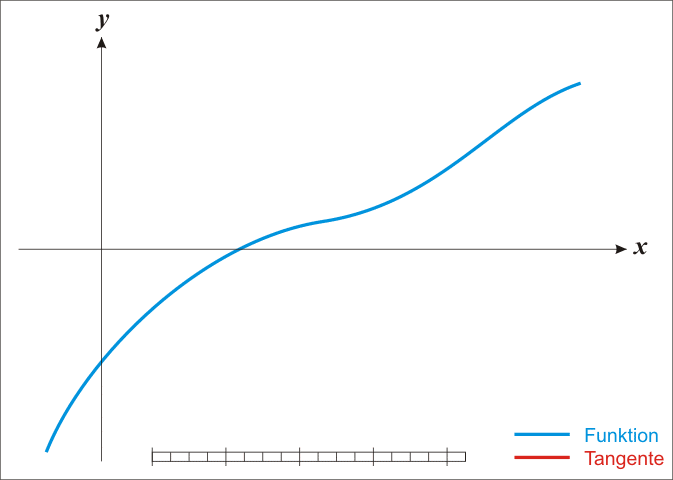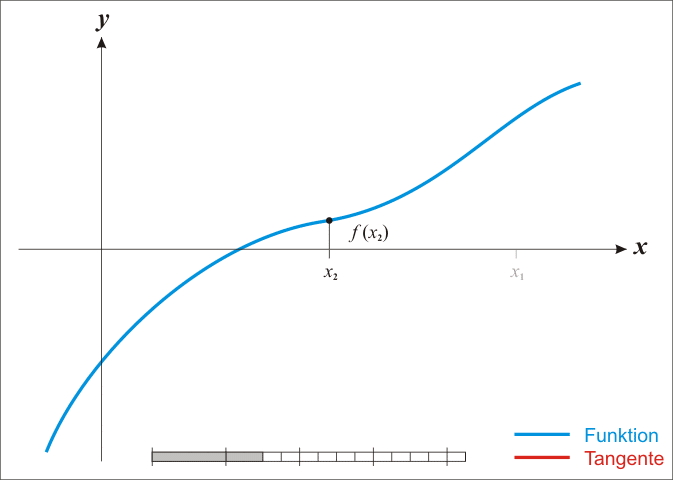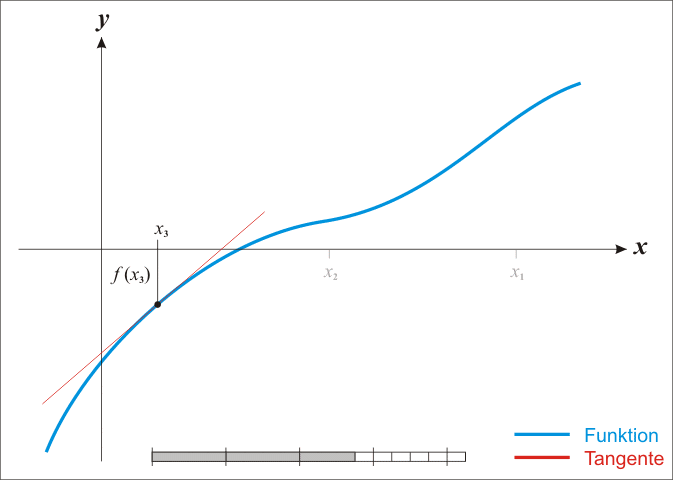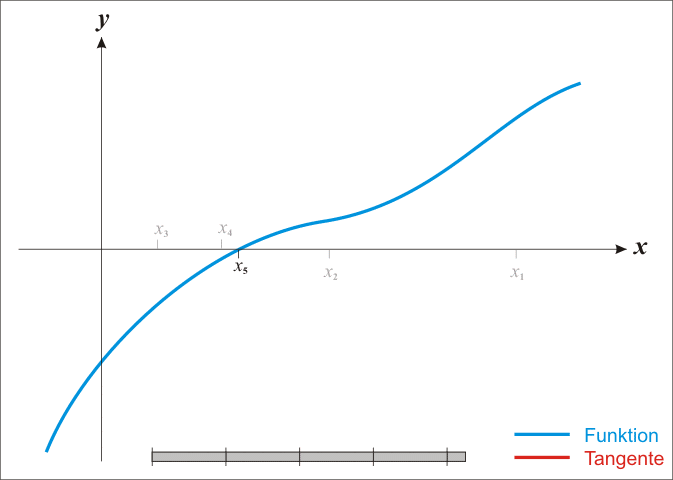
Anschaulich gelangt man wie folgt zu diesem Verfahren: Sei
eine stetig differenzierbare
reelle Funktion, von der wir eine Stelle
im Definitionsbereich
mit „kleinem“ Funktionswert kennen. Wir wollen einen Punkt
nahe
finden, der eine verbesserte Näherung der Nullstelle darstellt. Dazu
linearisieren wir die Funktion
an der Stelle
,
d.h. wir ersetzen sie durch ihre Tangente
im Punkt
mit Anstieg
.
Die Tangente ist durch die Funktion
gegeben. Setzen wir
ein, so erhalten wir
.
Wir wählen als
die einzige Nullstelle dieser linearen Funktion,
.
Wenden wir diese Konstruktion mehrfach an, so erhalten wir aus einer ersten
Stelle
eine unendliche Folge
von Stellen
,
die durch die Rekursionsvorschrift
definiert ist. Diese Vorschrift wird auch als Newtoniteration bezeichnet, die
Funktion
als Newtonoperator. Die Newtoniteration ist ein spezieller Fall einer Fixpunktiteration,
falls die Folge gegen
konvergiert,
so gilt
und daher
.
Die Kunst der Anwendung des Newtonverfahrens besteht darin, geeignete
Startwerte
zu finden. Je mehr über die Funktion
bekannt ist, desto kleiner lässt sich die notwendige Menge von Startwerten
gestalten.
Viele nichtlineare Gleichungen haben mehrere Lösungen, so hat ein Polynom -ten
Grades bis zu
Nullstellen. Will man alle Nullstellen in einem bestimmten Bereich
ermitteln, so muss zu jeder Nullstelle ein passender Startwert in
gefunden werden, für den die Newtoniteration konvergiert. Dazu könnte man
z.B. per Bisektion
genügend kleine isolierende Intervalle zu jeder Nullstelle bestimmen.
Erstes Beispiel
Die Quadratwurzel einer Zahl
ist die positive Nullstelle der Funktion
.
Diese Funktion hat die Ableitung
,
die Newtoniteration erfolgt also nach der Vorschrift
Der Vorteil dieser Vorschrift gegenüber dem Wurzelziehen nach Heron (siehe
unten) ist, dass es divisionsfrei ist, sobald einmal der Kehrwert von
bestimmt wurde. Als Startwert wurde in der Tabelle
gewählt. Die Iterierten wurden an der ersten ungenauen Stelle abgeschnitten. Es
ist zu erkennen, dass nach wenigen Schritten die Anzahl gültiger Stellen schnell
wächst.
| n | |||
| 0 | |||
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| 7 | |||
| 8 |
Betrachten wir die Differenz
zum Grenzwert im
-ten
Schritt, so kann mittels der binomischen Formeln die Differenz im
-ten
Schritt zweimal abgespalten werden:
Nach der Ungleichung
vom arithmetischen und geometrischen Mittel gilt ,
so dass der zweite Faktor sinnvoll durch
beschränkt werden kann. Ist die Differenz im
-ten
Schritt eine kleine Zahl, so ist die Differenz im
-ten
Schritt proportional zum Quadrat davon, also wesentlich kleiner. So entsteht
durch Quadrieren eines Fehlers
eine Fehlerabschätzung proportional zu
.
Deshalb spricht man davon, dass sich die Anzahl der gültigen Stellen in jedem
Schritt der Newtoniteration ungefähr verdoppelt.
Konvergenzbetrachtungen

Das Newtonverfahren ist ein sogenanntes lokal konvergentes Verfahren. Konvergenz der in der Newtoniteration erzeugten Folge zu einer Nullstelle ist also nur garantiert, wenn der Startwert, d.h. das 0-te Glied der Folge, schon „ausreichend nahe“ an der Nullstelle liegt. Ist der Startwert zu weit entfernt, ist das Konvergenzverhalten nicht festgelegt, das heißt, es ist sowohl eine Divergenz der Folge möglich als auch eine Oszillation (bei der sich endlich viele Funktionswerte abwechseln) oder eine Konvergenz gegen eine andere Nullstelle der betrachteten Funktion.
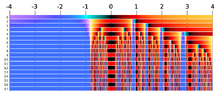
Ist der Startwert
so gewählt, dass das Newtonverfahren konvergiert, so ist die Konvergenz
allerdings quadratisch, also mit der Konvergenzordnung
2 (falls die Ableitung an der Nullstelle nicht verschwindet). Die Menge der
Startpunkte, für die das Newtonverfahren gegen eine bestimmte Nullstelle
konvergiert, bildet den Einzugsbereich dieser Nullstelle. Färbt man für eine Polynomfunktion, mit reellen
oder komplexen Koeffizienten, die Einzugsbereiche verschiedener Nullstellen in
der komplexen Ebene unterschiedlich ein, so ergibt sich ein Newtonfraktal. In diesem
ist zu erkennen, dass die Einzugsbereiche Bassins, d.h. Kreisscheiben um
die Nullstellen enthalten, aus welchen heraus die Newtoniteration stabil gegen
die Nullstelle im Zentrum konvergiert. Aber es ist auch zu erkennen, dass die
Ränder der Einzugsbereiche „ausgefranst“ sind, sie haben sogar eine fraktale Struktur. Geringe
Abweichungen im Startpunkt können also zu unterschiedlichen Nullstellen führen.
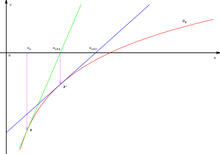
Falls es jedoch im Intervall
genau eine Nullstelle gibt, in
durchweg
sowie
gilt und der Startwert
links von der Nullstelle
gewählt wird, dann konvergiert die Folge im Newtonverfahren stets, und zwar
streng monoton wachsend (siehe Abbildung unten bzw. die Tabelle oben ab
).
Beispiele für Nicht-Konvergenz
- Oszillierendes Verhalten ergibt sich u.a. für das Polynom
mit
. Der Punkt
mit
und
wird durch den Newtonoperator auf den Punkt
abgebildet, der Punkt
wiederum, mit
und
, wird auf
abgebildet, so dass die Newtoniteration mit einem dieser Punkte als Startwert eine periodische Folge ergibt, diese beiden Punkte wechseln sich zyklisch ab. Dieser Zyklus ist stabil, er bildet einen Attraktor der Newtoniteration. Das bedeutet, um beide Punkte gibt es Umgebungen, so dass Startpunkte aus diesen Umgebungen gegen den Zyklus konvergieren und somit je einen der Punkte 0 und 1 als Grenzwert der Teilfolge mit geradem Index und der mit ungeradem Index haben.
- Divergenz bzw. beliebig weites Entfernen vom Startpunkt ergibt sich für
mit
und
. Es gibt eine Stelle
mit
d.h.
Man überzeugt sich, dass dann
gilt. Dieses Verhalten ist nicht stabil, denn bei leichter Variation des Anfangswertes, wie sie zum Beispiel durch die numerische Berechnung entsteht, entfernt sich die Newtoniteration immer weiter von der idealen divergierenden Folge. Selbst bei schließlicher Konvergenz wird die gefundene Nullstelle sehr weit vom Startwert entfernt sein.
Lokale quadratische Konvergenz
Sei
eine zweimal stetig differenzierbare reelle Funktion und
eine einfache Nullstelle von
,
in welcher die Ableitung somit keine Nullstelle hat. Das bedeutet, dass der
Graph der Funktion transversal, d.h. nicht-berührend, die
-Achse
schneidet. Sei
ein Punkt nahe bei
.
Dann kann die Taylorformel zweiten Grades (mit Lagrange-Restglied)
liegt zwischen
und
,
nach der Differenz
umgestellt werden,
.
Es wird nun so umgestellt, dass der Newtonoperator auf der rechten Seite erscheint,
.
Seien
ein Intervall um
ohne Nullstelle der Ableitung
und
sowie
Schranken der Ableitungen von
.
Dann folgt für alle
die Abschätzung
.
Mit
sei der konstante Faktor bezeichnet. In jedem Schritt
der Newtoniteration wird die Größe
kleiner sein als das Quadrat derselben Größe im vorhergehenden Schritt,
.
Nach vollständiger
Induktion ergibt sich
.
Kann also für den Startpunkt der Iteration die Abschätzung
garantiert werden, z.B. indem die Intervalllänge von
kleiner als
ist, so konvergiert die Folge
der Newtoniteration gegen die Nullstelle
,
denn die Folge
und damit
ist nach der angegebenen Abschätzung eine Nullfolge.
Die Verkürzung des Intervalls kann durch einige Iterationen eines langsameren
Verfahrens zur Nullstelleneinschränkung erreicht werden, z.B. des Bisektionsverfahrens
oder der Regula
falsi.
Die aus dieser Abschätzungen folgende Konvergenzgeschwindigkeit
wird als quadratisch bezeichnet, die (logarithmische) Genauigkeit bzw.
Anzahl gültiger Stellen verdoppelt sich in jedem Schritt. Die Abschätzung des
Abstands
zur Nullstelle wird oft linear in
angegeben, so gilt z.B.
, falls die Länge des Intervalls
kleiner als
ist. Dies ergibt eine Abschätzung der gültigen Stellen im Binärsystem.
, falls die Länge des Intervalls
kleiner als
ist, d.h. nahe genug an der Nullstelle ergibt sich eine Verdopplung der gültigen Dezimalstellen in jedem Schritt.
Lokale quadratische Konvergenz bei mehrfacher Nullstelle durch Modifikation
Für den Fall, dass
bei
eine mehrfache Nullstelle endlichen Grades besitzt, lässt sich ebenfalls die
Konvergenzgeschwindigkeit abschätzen und durch eine geringfügige Modifikation
wieder quadratische Konvergenz erzwingen.
Hat
bei
eine
-fache
Nullstelle, lässt sich
schreiben als
mit
.
Dann ist nach der Produktregel
und damit der Ausdruck
.
Setzt man dies nun in die Iteration ein, so erhält man
und daraus nach beidseitiger Subtraktion von
den Iterationsfehler
.
Wenn nun der Ausdruck
sehr klein geworden ist, wird der Summand
im Nenner viel kleiner als
,
so dass sich die hintere Klammer in
immer mehr dem Wert
nähert. Für die einfache Nullstelle mit
hat man einen kleinen Wert
,
der fast 0 wird, so dass
wird. Für
wird
ungefähr 0,5, so dass sich der Abstand zur Nullstelle von Schritt zu Schritt nur
etwa halbiert und man nach etwa 10 Schritten die Genauigkeit nur in weiteren
drei Dezimalstellen erhöht hat. Bei
wird
etwa 0,67, so dass erst nach etwa 16 Schritten die Genauigkeit um weitere drei
Dezimalstellen steigt usw.
Man kann daher am Konvergenzverhalten die Vielfachheit der Nullstelle abschätzen, falls man sie nicht aus anderen Gründen weiß, und – wie nun noch beschrieben – das Verfahren optimieren.
Bei einer -fachen
Nullstelle modifiziert man das newtonsche Näherungsverfahren mit einem Faktor
:
(Newtonverfahren bei
-facher Nullstelle)
Damit wird dann
zu
Ist nun
wieder sehr klein, so wird im Nenner der Summand
viel kleiner als
, und man erhält
,
wobei der rechte Faktor wegen
gegen einen festen Wert konvergiert. Wie man sieht, liegt nun auch hier
quadratische Konvergenz vor.
Ein Beispiel zeigt das Konvergenzverhalten sehr schön. Die Funktion
hat die einfache Nullstelle
.
Die linke Spalte der Tabelle zeigt die rasche Konvergenz für den Startwert 1,
nach 4 Schritten lässt sich die Genauigkeit nicht mehr steigern, beim Fehler
verdoppelt sich die Anzahl der Nullen hinterm Komma (mindestens). Quadriert man
nun die Funktion (mittlere Spalte), wird die Nullstelle eine doppelte, und nun
zeigt sich das oben erläuterte Verhalten, dass sich ohne Modifikation der Fehler
in jedem Schritt nur etwa halbiert. Modifiziert man dann diesen Fall mit dem
Faktor
,
so stellt sich dasselbe Verhalten wie bei der einfachen Nullstelle ein (rechte
Spalte).
| n | Fehler | Fehler | Fehler | |||
| 0 | ||||||
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 | ||||||
| 7 | ||||||
| 8 | ||||||
| 9 | ||||||
| 10 |
Das Newtonverfahren für komplexe Zahlen
Für komplexe
Zahlen
schreibt man die Formel entsprechend:
mit der holomorphen
Funktion .
Die Zerlegung in Real- und Imaginärteil ergibt
Die komplexe Ableitung ist unabhängig von der Richtung der Ableitung an der
Stelle
d.h. es gilt
Daher gelten die Cauchy-Riemann'schen Differentialgleichungen
und
Die komplexe Gleichung (1) kann in Real- und Imaginärteil zerlegt werden:
.
Mit Hilfe (2) folgt hieraus
Die geometrische Bedeutung dieser Gleichung sieht man wie folgt. Man bestimmt
das Minimum vom Betrag .
Das Minimum wird für
angenommen. Dies kann mit dem Gradientenverfahren,
d.h. mit der Methode des steilsten Abstiegs bestimmt werden.
Man führt die Bezeichnung
ein. Die Formel für diese Methode lautet mit dem Vektor
:
Dies ist mit der Formel (1) identisch.
Bemerkungen
- Der lokale Konvergenzbeweis kann auch auf die gleiche Weise im
mehrdimensionalen Fall geführt werden, allerdings ist er dann technisch etwas
schwieriger, da mit zwei- und dreistufigen Tensoren für die erste bzw. zweite
Ableitung gearbeitet wird. Im Wesentlichen ist die Konstante K durch
zu ersetzen, mit geeigneten induzierten Operatornormen.
- Der lokale Konvergenzbeweis setzt voraus, dass ein eine Nullstelle enthaltendes Intervall bekannt ist. Aus seinem Beweis ergibt sich aber keine Möglichkeit, dies schnell zu testen. Ein Konvergenzbeweis, der auch hierfür ein Kriterium liefert, wurde zuerst von Leonid Kantorowitsch geführt und ist als Satz von Kantorowitsch bekannt.
- Um einen geeigneten Startpunkt zu finden, verwendet man gelegentlich andere („gröbere“) Verfahren. Beispielsweise kann man mit dem Gradientenverfahren eine ungefähre Lösung ermitteln und diese dann mit dem Newtonverfahren verfeinern.
- Bei unbekanntem Startpunkt kann man mittels einer Homotopie die Funktion
, von der man eine Nullstelle sucht, zu einer einfacheren Funktion
deformieren, von der (mindestens) eine Nullstelle bekannt ist. Man durchläuft dann die Deformation rückwärts in Form einer endlichen Folge sich nur „wenig“ unterscheidender Funktionen. Von der ersten Funktion
kennt man eine Nullstelle. Als Startwert der Newtoniteration zur gerade aktuellen Funktion der Folge verwendet man die Näherung einer Nullstelle der in der Folge vorhergehenden Funktion. Zum genauen Vorgehen siehe Homotopieverfahren.
-
- Als Beispiel mag die „Flutungshomotopie“ dienen: mit einem willkürlichen
bilden wir die Ausgangsfunktion
mit bekannter Nullstelle
. Wir haben den „Wasserspiegel“ vom „Nullpegel“ auf die Höhe
geflutet. Nun senken wir schrittweise den Wasserstand,
,
,
. In jedem Schritt wird eine Näherung
einer Nullstelle bestimmt, wobei
gesetzt wird. Es ist
und somit
eine der gesuchten Näherungslösungen.
- Als Beispiel mag die „Flutungshomotopie“ dienen: mit einem willkürlichen
Abbruchkriterien
Mögliche Abbruchkriterien bezüglich einer Restgröße (zum Beispiel Rechner-Arithmetik) sind:
Wobei
die Qualität der „Nullstelle“ bestimmt. In beiden Fällen kann es vorkommen, dass
das Abbruchkriterium zu einem „schlechten“ Zeitpunkt erfüllt ist.
Weitere Anwendungsbeispiele
Lösen eines Optimierungsproblems
Das Newtonverfahren kann verwendet werden, um einen Extremwert einer Funktion
zu finden. Dafür sucht man mit dem Verfahren nach einem Kritischen
Punkt, d.h. nach einer Nullstelle in der ersten Ableitung der
Funktion. Der Iterationsschritt sieht demnach wie folgt aus:
Für eine Funktion
mit mehreren Eingangsvariablen
verwendet man analog die Jacobimatrix
und die inverse Hessematrix
(siehe auch Das
Newtonverfahren im Mehrdimensionalen):
Berechnung der Quadratwurzel
Ein Spezialfall des newtonschen Näherungsverfahrens ist das babylonische Wurzelziehen, auch bekannt als Heronverfahren nach Heron von Alexandria:
Wendet man die Iterationsformel zur Nullstellenbestimmung auf die Funktion
an, so erhält man wegen der Ableitungsfunktion
für die Lösung
das Näherungsverfahren
.
Dieses Verfahren konvergiert für jedes
und für jeden beliebigen Anfangswert
.
Berechnung der Kubikwurzel
Wendet man die Iterationsformel zur Nullstellenbestimmung auf die Funktion
an, so erhält man wegen der Ableitungsfunktion
für die Lösung
das Näherungsverfahren
.
Für negative Radikanden empfiehlt sich die Umrechnung mit .
Dieses Verfahren konvergiert für
und Anfangswert
,
wenn
und
gleiches Vorzeichen haben.
Schnittpunkt zweier Funktionen
Auf ähnliche Weise lässt sich auch der -Wert
des Schnittpunktes zweier Funktionen
und
bestimmen:
Da man die beiden Funktionen zur Lösung des Problems gleichsetzt, lässt sich immer durch Umformung folgende Form, auf die das newtonsche Näherungsverfahren angewendet werden kann, bestimmen:
Gemischt-goniometrische Funktion
Gesucht sei die positive Lösung
der Gleichung
.
Das Problem kann umformuliert werden als
.
Gesucht werden also Nullstellen von
.
Wir haben nun .
Da
für alle
gilt und
für
,
wissen wir, dass die Nullstelle zwischen 0 und 1 liegt. Wir starten die
Iteration mit dem Wert
.
Damit sind die ersten zwölf Ziffern der Nullstelle bekannt.
Das Newton-Verfahren im Mehrdimensionalen
Das Newtonverfahren kann auch benutzt werden, um Nullstellen von
mehrdimensionalen Funktionen
zu bestimmen. Ein konkreter Anwendungsfall ist die Kombination mit der Gaußschen
Fehlerquadratmethode im Gauß-Newton-Verfahren.
Für den allgemeinen Fall ist der Ausgangspunkt eine Taylorentwicklung
der Funktion
:
wobei
die Jacobimatrix,
also die Matrix der partiellen
Ableitungen von
,
ist:
Anstatt nach Nullstellen der nicht-linearen Funktion
zu suchen, sucht man nach Nullstellen der linearen Anpassung von
im Punkt
:
Für
und
inspiriert dies das Newtonverfahren:
Da das Lösen von
über die Berechnung der Inversen
einer Matrix und anschließender Multiplikation mit
aufwendiger und numerisch ungünstiger ist, wird stattdessen das lineare
Gleichungssystem
gelöst. Danach erhält man
aus:
Zum Lösen des Systems existieren verschiedene Lösungsverfahren. Ist die Jacobimatrix in der Nullstelle invertierbar und in einer Umgebung der Nullstelle lipschitzstetig, so konvergiert das Verfahren lokal quadratisch.
Varianten des Newtonverfahrens
Das größte Problem bei der Anwendung des Newtonverfahrens liegt darin, dass
man die erste Ableitung der Funktion benötigt. Deren Berechnung ist meist
aufwendig, und in vielen Anwendungen ist eine Funktion auch nicht analytisch
gegeben, sondern beispielsweise nur durch ein Computerprogramm. Im Eindimensionalen ist dann die Regula falsi vorzuziehen,
bei der die Sekante und nicht die Tangente benutzt wird. Im Mehrdimensionalen
muss man andere Alternativen suchen. Hier ist das Problem auch dramatischer, da
die Ableitung eine Matrix mit
Einträgen ist, der Aufwand der Berechnung steigt also quadratisch mit der
Dimension.
Vereinfachtes Newtonverfahren
Statt die Ableitung in jedem Newton-Schritt auszurechnen, ist es auch möglich, sie nur in jedem n-ten Schritt zu berechnen. Dies senkt die Kosten für einen Iterationsschritt drastisch, der Preis ist ein Verlust an Konvergenzgeschwindigkeit. Die Konvergenz ist dann nicht mehr quadratisch, es kann aber weiterhin superlineare Konvergenz erreicht werden.
Inexaktes Newtonverfahren
Eine ähnliche Idee besteht darin, in jedem Schritt eine Approximation der Ableitung zu berechnen, beispielsweise über finite Differenzen. Eine quantitative Konvergenzaussage ist in diesem Fall schwierig, als Faustregel lässt sich jedoch sagen, dass, je schlechter die Approximation der Ableitung ist, desto schlechter die Konvergenz wird. Ein Beispiel für ein solches Verfahren ist das Sekantenverfahren.
Newton-Krylow-Verfahren
Für die numerische Lösung nichtlinearer partieller Differentialgleichungen bietet sich prinzipiell das Newtonverfahren als Grundlöser an. Die entsprechende Jacobimatrix ist immer dünnbesetzt, und daher bieten sich Krylow-Unterraum-Verfahren zur Lösung der linearen Gleichungssysteme an. Man spricht dann von Newton-Krylow-Verfahren. Im Krylowverfahren selbst tritt die Jacobimatrix nur in Matrix-Vektorprodukten auf, welche als Richtungsableitungen interpretiert werden können. Approximiert man diese durch finite Differenzen, so erhält man matrixfreie Verfahren.
Literatur
- P. Deuflhard, A. Hohmann: Numerische Mathematik I. Eine algorithmisch orientierte Einführung. 3. überarbeitete und erweiterte Auflage. De Gruyter, Berlin, New York 2002, ISBN 3-11-017182-1.
- M. Hermann: Numerische Mathematik, Band 1: Algebraische Probleme. 4., überarbeitete und erweiterte Auflage. Walter de Gruyter Verlag, Berlin und Boston 2020, ISBN 978-3-11-065665-7.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 13.07. 2022