Holomorphe Funktion

Ein rechteckiges Gitter wird mit der holomorphen Funktion in sein Abbild überführt

Holomorphie (von gr. ὅλος holos, „ganz“ und μορφή morphe, „Form“) ist eine Eigenschaft von bestimmten komplexwertigen Funktionen, die in der Funktionentheorie (einem Teilgebiet der Mathematik) behandelt werden. Eine Funktion $f\colon U\to {\mathbb {C}}$ mit einer offenen Menge $U\subseteq \mathbb {C}$ heißt holomorph, falls sie in jedem Punkt von komplex differenzierbar ist. Insbesondere in älterer Literatur werden solche Funktionen auch regulär genannt.

Auch wenn die Definition analog zur reellen Differenzierbarkeit ist, zeigt sich in der Funktionentheorie, dass die Holomorphie eine sehr starke Eigenschaft ist. Sie produziert nämlich eine Vielzahl von Phänomenen, die im Reellen kein Pendant besitzen. Beispielsweise ist jede holomorphe Funktion beliebig oft (stetig) differenzierbar und lässt sich lokal in jedem Punkt in eine Potenzreihe entwickeln.

Definitionen

Es sei $U\subseteq \mathbb {C}$ eine offene Teilmenge der komplexen Ebene und $z_{0}\in U$ ein Punkt dieser Teilmenge. Eine Funktion $f\colon U\to {\mathbb {C}}$ heißt komplex differenzierbar im Punkt $z_{0}$ , falls der Grenzwert

$\lim _{h\to 0}{\frac {f(z_{0}+h)-f(z_{0})}{h}}$

existiert. Man bezeichnet ihn dann als $f'(z_{0})$ .

Die Funktion heißt holomorph im Punkt $z_{0}$ , falls eine Umgebung von $z_{0}$ existiert, in der komplex differenzierbar ist. Ist auf ganz holomorph, so nennt man holomorph. Ist weiter $U={\mathbb {C}}$ , so nennt man eine ganze Funktion.

Erläuterungen

Zusammenhang zwischen komplexer und reeller Differenzierbarkeit

$\mathbb {C}$ ist in natürlicher Weise ein zweidimensionaler reeller Vektorraum mit der kanonischen Basis $\{1,i\}$ und so kann man eine Funktion $f\colon U\to {\mathbb {C}}$ auf einer offenen Menge $U\subseteq \mathbb {C}$ auch auf ihre totale Differenzierbarkeit im Sinne der mehrdimensionalen reellen Analysis untersuchen. Bekanntlich heißt (total) differenzierbar in $z_{0}$ , falls eine $\mathbb {R}$ -lineare Abbildung existiert, sodass

$f(z_{0}+h)=f(z_{0})+L(h)+r(h)$

gilt, wobei eine Funktion mit

$\lim _{h\to 0}{\frac {r(h)}{|h|}}=0$

ist. Nun sieht man, dass die Funktion genau dann in $z_{0}$ komplex differenzierbar ist, wenn sie dort total differenzierbar ist und sogar $\mathbb {C}$ -linear ist. Letzteres ist eine starke Bedingung. Sie bedeutet, dass die Darstellungsmatrix von bezüglich der kanonischen Basis $\{1,i\}$ die Form

${\begin{pmatrix}a&-b\\b&a\end{pmatrix}}$

hat.

Cauchy-Riemannsche Differentialgleichungen

→ Hauptartikel: Cauchy-Riemannsche partielle Differentialgleichungen

Zerlegt man nun eine Funktion $f\left(x+iy\right)=u\left(x,y\right)+i\,v\left(x,y\right)$ in ihren Real- und Imaginärteil mit reellen Funktionen u,v , so hat die totale Ableitung als Darstellungsmatrix die Jacobi-Matrix

${\begin{pmatrix}{\frac {\partial u}{\partial x}}&{\frac {\partial u}{\partial y}}\\{\frac {\partial v}{\partial x}}&{\frac {\partial v}{\partial y}}\end{pmatrix}}.$

Folglich ist die Funktion genau dann komplex differenzierbar, wenn sie reell differenzierbar ist und für u,v die Cauchy-Riemannschen Differentialgleichungen

${\frac {\partial u}{\partial x}}={\frac {\partial v}{\partial y}}$

$\displaystyle {\frac {\partial u}{\partial y}}=-{\frac {\partial v}{\partial x}}$

erfüllt sind.

Äquivalente Eigenschaften holomorpher Funktionen einer Variablen

In einer Umgebung einer komplexen Zahl sind folgende Eigenschaften komplexer Funktionen gleichwertig:

Die Funktion ist einmal komplex differenzierbar.
Die Funktion ist beliebig oft komplex differenzierbar.
Real- und Imaginärteil erfüllen die Cauchy-Riemannschen Differentialgleichungen und sind zumindest einmal stetig reell-differenzierbar.
Die Funktion lässt sich in eine komplexe Potenzreihe entwickeln.
Die Funktion ist stetig und das Wegintegral der Funktion über einen beliebigen geschlossenen zusammenziehbaren Weg verschwindet.
Die Funktionswerte im Inneren einer Kreisscheibe lassen sich aus den Funktionswerten am Rand mit Hilfe der cauchyschen Integralformel ermitteln.
Die Funktion ist reell differenzierbar und es gilt
$\quad {\frac {\partial f}{\partial {\bar {z}}}}=0,$
wobei ${\tfrac {\partial }{\partial {\bar z}}}$ der Cauchy-Riemann-Operator ist, der durch ${\tfrac {\partial }{\partial {\bar {z}}}}:={\tfrac {1}{2}}\left({\tfrac {\partial }{\partial x}}+i{\tfrac {\partial }{\partial y}}\right)$ definiert ist.

Beispiele

Ganze Funktionen

Ganze Funktionen sind auf ganz $\mathbb {C}$ holomorph. Beispiele dafür sind

jedes Polynom $\textstyle z\mapsto \sum _{{j=0}}^{n}a_{j}z^{j}$ mit Koeffizienten $a_{j}\in {\mathbb {C}}$ ,
die Exponentialfunktion $\exp$ ,
die trigonometrischen Funktionen $\sin$ und $\cos$ ,
die hyperbolischen Funktionen $\sinh$ und $\cosh$ .

Holomorphe, nichtganze Funktionen

Gebrochen rationale Funktionen sind holomorph außer an den Nullstellen ihres Nennerpolynoms. Dort besitzen sie isolierte Singularitäten. Wenn diese nicht hebbar sind, handelt es sich um Polstellen, sodass dann Beispiele für meromorphe Funktionen vorliegen.
Die Logarithmusfunktion $\log$ lässt sich in allen Punkten aus $\mathbb {C} \setminus {]{-\infty },0]}$ in eine Potenzreihe entwickeln und ist somit auf der Menge $\mathbb {C} \setminus {]{-\infty },0]}$ holomorph.

Nirgends holomorphe Funktionen

In keinem $z\in\mathbb{C}$ komplex differenzierbar und damit auch nirgendwo holomorph sind beispielsweise

die Betragsfunktion $z\mapsto |z|$ ,
die Projektionen auf den Realteil $z\mapsto {\mathrm {Re}}(z)$ beziehungsweise auf den Imaginärteil $z\mapsto {\mathrm {Im}}(z)$ ,
die komplexe Konjugation $z\mapsto \overline {z}$ .

Die Funktion $z\mapsto |z|^{2}$ ist nur an der Stelle z=0 komplex differenzierbar, aber dort nicht holomorph, da sie nicht in einer ganzen Umgebung von $0$ komplex differenzierbar ist.

Eigenschaften

Sind $f,g\colon U\to \mathbb {C}$ an einer Stelle $z \in U$ komplex differenzierbar, so auch f+g , f-g und $f\cdot g$ . Das gilt auch für ${\tfrac {f}{g}}$ , wenn keine Nullstelle von ist. Es gelten ferner Summen-, Produkt-, Quotienten- und Kettenregel.

Es folgt eine Auflistung fundamentaler Eigenschaften holomorpher Funktionen, die alle keine Entsprechung in der reellen Theorie besitzen. In der Folge sei $U\subseteq \mathbb {C}$ ein Gebiet und $f\colon U\to \mathbb {C}$ holomorph.

Cauchyscher Integralsatz

→ Hauptartikel: Cauchyscher Integralsatz

Ist $U\subseteq \mathbb {C}$ einfach zusammenhängend und $\gamma$ ein Zyklus in , so gilt der cauchysche Integralsatz

$\int _{\gamma }f(z)\,\mathrm {d} z=0.$

Der Satz gilt also insbesondere dann, wenn ein Sterngebiet und $\gamma$ ein geschlossener Weg ist.

Cauchysche Integralformel

→ Hauptartikel: Cauchysche Integralformel

Sei $D:=U_{r}(a)$ die offene Kreisscheibe mit Radius um den Punkt $a\in U$ . Liegt der Abschluss von noch ganz in , so gilt für alle $z\in D$ und $k\in \mathbb{N} _{0}$ die cauchysche Integralformel

$f^{{(k)}}(z)={\frac {k!}{2\pi i}}\int _{{\partial D}}{\frac {f(\zeta )}{(\zeta -z)^{{k+1}}}}{\mathrm d}\zeta .$

Der Wert der Funktion (und jeder ihrer Ableitungen) eines Punktes in einem Gebiet hängt also nur von den Funktionswerten am Rand dieses Gebietes ab.

Holomorphie und Analytizität

Eine Folgerung aus der cauchyschen Integralformel ist, dass in der komplexen Ebene der Begriff der Analytizität äquivalent zur Holomorphie ist: Jede in $z_{0}$ holomorphe Funktion ist in $z_{0}$ analytisch. Umgekehrt lässt sich jede in $z_{0}$ analytische Funktion zu einer in $z_{0}$ holomorphen Funktion fortsetzen.

Da Potenzreihen beliebig oft komplex differenzierbar sind (und zwar durch gliedweise Differentiation), erhält man insbesondere, dass holomorphe Funktionen beliebig oft differenzierbar und alle ihre Ableitungen wiederum holomorphe Funktionen sind. Hieran erkennt man schon deutliche Unterschiede zur reellen Differentialrechnung.

Identitätssatz

Es zeigt sich, dass eine holomorphe Funktion schon durch sehr wenig Information eindeutig bestimmt ist. Der Identitätssatz besagt, dass zwei holomorphe Funktionen auf einem Gebiet $G\subseteq \mathbb {C}$ bereits dann auf ganz identisch sind, wenn sie auf einer geeigneten echten Teilmenge $M\subset G$ übereinstimmen. Dabei muss die Übereinstimmungsmenge noch nicht einmal ein kontinuierlicher Weg sein: Es reicht aus, dass einen Häufungspunkt in besitzt. Diskrete Teilmengen reichen hierfür hingegen nicht aus.

Weiteres

Der Satz von Liouville besagt, dass jede beschränkte ganze Funktion konstant ist. Eine einfache Folgerung hieraus ist der Fundamentalsatz der Algebra.
Satz von der Gebietstreue: Ist $U\subseteq \mathbb {C}$ ein Gebiet und $f\colon U\to \mathbb {C}$ nicht konstant, dann ist $f(U)\subseteq \mathbb {C}$ wieder ein Gebiet.
Eine Folgerung der Gebietstreue ist das Maximumprinzip.
Satz von Weierstraß: Konvergiert eine Folge $(f_{n})_{{n\in {\mathbb {N}}}}$ holomorpher Funktionen kompakt auf gegen die Grenzfunktion , so ist wieder holomorph und man kann Limesbildung und Differentiation vertauschen, das heißt, die Folge $(f'_{n})$ konvergiert kompakt gegen .
Satz von Montel: Ist die Folge $(f_{n})_{{n\in {\mathbb {N}}}}$ holomorpher Funktionen auf lokal beschränkt, so existiert eine kompakt konvergente Teilfolge.
Jede auf einem einfach zusammenhängenden Gebiet $D\subseteq \mathbb {R} ^{2}$ zweimal stetig differenzierbare harmonische Funktion ist Realteil einer komplex differenzierbaren Funktion $f\colon x+\mathrm {i} y\mapsto u(x,y)+\mathrm {i} v(x,y)$ . Die reelle Funktion $v=\operatorname {Im}f$ erfüllt ebenfalls $\Delta v=0$ . Sie wird als konjugiert harmonisch zu bezeichnet und als komplexes Potential.

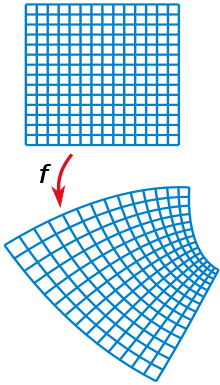
Biholomorphe Funktionen

→ Hauptartikel: Biholomorphe Funktion

Eine Funktion, die holomorph, bijektiv und deren Umkehrfunktion holomorph ist, nennt man biholomorph. Im Fall einer komplexen Veränderlichen ist das äquivalent dazu, dass die Abbildung bijektiv und konform ist. Aus dem Satz über implizite Funktionen folgt für holomorphe Funktionen einer Veränderlicher schon, dass eine bijektive, holomorphe Funktion stets eine holomorphe Umkehrabbildung besitzt. Im nächsten Abschnitt werden holomorphe Funktionen mehrerer Veränderlicher eingeführt. In diesem Fall garantiert der Satz von Osgood diese Eigenschaft. Somit kann man sagen, dass bijektive, holomorphe Abbildung biholomorph sind.

Aus Sicht der Kategorientheorie ist eine biholomorphe Abbildung ein Isomorphismus.

Holomorphie mehrerer Veränderlicher

Im n-dimensionalen komplexen Raum

Sei $D\subseteq \mathbb {C} ^{n}$ eine offene Teilmenge. Eine Abbildung $f\colon D\to \mathbb {C}$ heißt holomorph, falls sie sich um jeden Punkt des Definitionsbereichs in eine Potenzreihe entwickeln lässt, das heißt, zu jedem $w=(w_{1},\dotsc ,w_{n})\in D$ gibt es einen Polykreis $\Delta (w;r_{1},\dotsc ,r_{n})\subset D$ , sodass

$f(z)=\sum _{k_{1},\dotsc ,k_{n}=0}^{\infty }a_{k_{1},\dotsc ,k_{n}}(z_{1}-w_{1})^{k_{1}}\cdots (z_{n}-w_{n})^{k_{n}}$

für alle $z\in \Delta (w;r_{1},\dotsc ,r_{n})$ mit von unabhängigen Koeffizienten $a_{k_{1},\dotsc ,k_{n}}\in \mathbb {C}$ gilt. Eine Funktion $f\colon D\to \mathbb {C}$ heißt holomorph in der -ten Variablen, wenn sie als Funktion von z_j bei festgehaltenen übrigen Variablen holomorph ist. Holomorphe Funktionen sind natürlich in jeder Variablen holomorph. Für die Umkehrung siehe die untenstehenden äquivalenten Charakterisierungen.

Mit dem Wirtinger-Kalkül $\textstyle {\frac {\partial }{\partial z^{j}}}$ und $\textstyle {\frac {\partial }{\partial \overline {z}^{j}}}$ steht ein Kalkül zur Verfügung, mit dem man die partiellen Ableitungen einer komplexen Funktion wie bei Funktionen einer Veränderlichen behandeln kann.

Für eine Funktion $f\colon D\to \mathbb {C}$ , $D\subseteq \mathbb {C} ^{n}$ offen, sind folgende Aussagen äquivalent:

ist holomorph.
ist stetig und holomorph in jeder Variablen (Lemma von Osgood)
ist holomorph in jeder Variablen (Satz von Hartogs)
ist stetig differenzierbar und genügt den cauchy-riemannschen Differentialgleichungen $\textstyle {\frac {\partial }{\partial {\overline {z}}^{j}}}f=0$ für $j=1,\dotsc ,n$ .

Für mehrere Dimensionen im Bildbereich definiert man Holomorphie wie folgt: Eine Abbildung $f=(f_{1},\dotsc ,f_{m})\colon D\to \mathbb {C} ^{m}$ , $D\subseteq \mathbb {C} ^{n}$ offen, heißt holomorph, wenn jede der Teilfunktionen $f_{j}\colon D\to \mathbb {C}$ holomorph ist.

Viele Eigenschaften holomorpher Funktionen einer Veränderlichen lassen sich, teils in abgeschwächter Form, auf den Fall mehrerer Veränderlicher übertragen. So gilt für Funktionen $f\colon D\to \mathbb {C} ^{m}$ der cauchysche Integralsatz nicht und der Identitätssatz ist nur noch in einer abgeschwächten Version gültig. Für diese Funktionen kann allerdings die Integralformel von Cauchy durch Induktion auf Dimensionen verallgemeinert werden. Salomon Bochner konnte 1944 sogar noch eine Verallgemeinerung der -dimensionalen cauchyschen Integralformel beweisen. Diese trägt den Namen Bochner-Martinelli-Formel.

In der komplexen Geometrie

Auch in der komplexen Geometrie werden holomorphe Abbildungen betrachtet. So kann man holomorphe Abbildungen zwischen riemannschen Flächen oder zwischen komplexen Mannigfaltigkeiten analog zu differenzierbaren Funktionen zwischen glatten Mannigfaltigkeiten definieren. Außerdem gibt es ein für die Integrationstheorie wichtiges Pendant zu den glatten Differentialformen, das holomorphe Differentialform heißt.

Basierend auf einem Artikel in:

Wikipedia.de