Fundamentalsatz der Algebra

Der (Gauß-d’Alembertsche) Fundamentalsatz der Algebra besagt, dass jedes nicht konstante Polynom im Bereich der komplexen Zahlen mindestens eine Nullstelle besitzt. Dabei können die Koeffizienten des Polynoms beliebige komplexe Zahlen sein – insbesondere sind Polynome mit ganzen oder reellen Koeffizienten mit eingeschlossen.

Wendet man den Satz zum Beispiel auf das Polynom z^4+15z^2+4 an, so folgt, dass die im Bereich der reellen Zahlen unlösbare Gleichung z^4+15z^2+4 = 0 im Bereich der komplexen Zahlen mindestens eine Lösung besitzen muss.

Der Fundamentalsatz der Algebra sagt, dass die komplexen Zahlen algebraisch abgeschlossen sind.

Die Namensgebung wurzelt in einem traditionellen Verständnis der Algebra als der Lehre von Gleichungen höheren Grades mittels „Buchstabenrechnen“.

Satz

Es sei

$P(z) = \sum_{k=0}^n a_k \cdot z^k$

ein Polynom vom Grad $\deg P=:n\in \mathbb {N} \backslash \{0\}$ – also ein nicht konstantes Polynom – mit komplexen Koeffizienten $a_k \in \mathbb C$ . Dann hat das Polynom eine komplexe Nullstelle, d.h., es gibt eine Zahl $z \in \mathbb C$ , so dass P(z) = 0 gilt. Genauer gilt insbesondere, dass die Anzahl der Nullstellen, wenn sie mit der richtigen Vielfachheit gezählt werden, insgesamt gleich dem Grad des Polynoms ist.

Anmerkung zum Fall reeller Koeffizienten

Auch wenn ein Polynom über den reellen Zahlen ist, wenn also alle Koeffizienten $a_{k}$ in $\mathbb {R}$ liegen, sind die zugehörigen Nullstellen nicht notwendigerweise reell. Es gilt aber: Ist eine nichtreelle Nullstelle von , so ist auch ihr komplex Konjugiertes $\bar{w}$ eine Nullstelle von . Ist eine mehrfache Nullstelle von , so hat $\bar{w}$ dieselbe Vielfachheit. In der faktorisierten Schreibweise des Polynoms lassen sich daher die zugehörigen Linearfaktoren immer zu einem quadratischen Faktor $(z-w)(z-\bar{w})$ zusammenfassen. Ausmultipliziert hat dieses Polynom zweiten Grades wieder rein reelle Koeffizienten:

$(z-w)(z-\bar{w}) = z^2 - (w+\bar{w})z + w\cdot\bar{w} = z^2 - 2\operatorname{Re}(w)\cdot z + |w|^2$

Daraus folgt im Umkehrschluss, dass jedes reelle Polynom sich in reelle Polynomfaktoren vom Grad eins oder zwei zerlegen lässt. In dieser Form wurde der Satz 1799 von Carl Friedrich Gauß im Rahmen seiner Doktorarbeit formuliert, die dieses Ergebnis bereits in ihrem lateinischen Titel Demonstratio nova theorematis omnem functionem algebraicam rationalem integram unius variabilis in factores reales primi vel secundi gradus resolvi posse verkündet (deutsch: Neuer Beweis des Satzes, dass jede ganze rationale algebraische Funktion in einer Variablen in reelle Faktoren ersten oder zweiten Grades zerlegt werden kann.)

Folgerung: Algebraische Abgeschlossenheit des komplexen Zahlkörpers

Von einem Polynom f(z) lässt sich der zu einer Nullstelle $z_{0}$ mit f(z_0)=0 gehörende Linearfaktor (z-z_0) abspalten: $f(z)=(z-z_{0})\cdot f'(z)$ . (Dazu kann beispielsweise die Horner-Ruffini-Methode verwendet werden.) Durch die Abspaltung ergibt sich ein im Grad um eins reduziertes Polynom f'(z) , für welches das Verfahren wiederholen werden kann. Per Induktion ist hiermit gezeigt: Jedes nicht konstante Polynom über $\mathbb {C}$ zerfällt vollständig in ein Produkt aus Linearfaktoren:

$f(z) = \sum_{k=0}^n a_k \cdot z^k = a_n \cdot \prod_{i=1}^n (z-z_i)$ ,

wobei die $z_{i}$ die Nullstellen des Polynoms sind.

Der Fundamentalsatz der Algebra besagt also, dass der Körper $\mathbb {C}$ der komplexen Zahlen algebraisch abgeschlossen ist.

Beispiel

Die Polynomgleichung

hat die Lösungen

$L=\{0^{(2)},1,2-3{\text{i}},2+3{\text{i}}\}$ ,

die natürlich die Nullstellen des Polynomes sind. Die Lösung 0 wird dabei doppelt gezählt, wie anhand der Faktorisierung des Polynoms ersichtlich ist:

$P(x)=x\cdot x\cdot(x-1)\cdot(x-2+3\text{i})\cdot(x-2-3\text{i}) = x\cdot x\cdot(x-1)\cdot(x^2-4x+13)$ .

Man verwendet auch die Sprechweise „0 tritt mit Vielfachheit 2 auf“, alle anderen Nullstellen treten mit Vielfachheit 1 auf. Dieses Beispiel zeigt auch, dass die Nullstellen im Allgemeinen nicht (alle) reell sind, selbst wenn das Polynom reelle Koeffizienten hat. Nichtreelle Nullstellen von Polynomen mit reellen Koeffizienten treten aber immer paarweise komplex konjugiert auf (in obigem Beispiel $2\pm 3i$ ).

Beweise

Geschichte und Überblick

Erste Formulierungen des Fundamentalsatzes finden sich im 17. Jahrhundert (Peter Roth, Albert Girard, René Descartes). Peter Roth (1608) vermutete, dass Gleichungen -ten Grades höchstens Lösungen haben, und Francois Viète gab Beispiele von Gleichungen -ten Grades mit der maximalen Anzahl von Lösungen an. Albert Girard vermutete 1629 (L'invention en l'algèbre) als Erster, dass es immer Lösungen gibt, und vermutete schon neben reellen auch komplexe Lösungen. Leonhard Euler gab eine Formulierung des Fundamentalsatzes als vollständige Faktorisierung im Komplexen im heutigen Sinn an. Der erste veröffentlichte Beweis von Jean d’Alembert 1746 war von der Idee her korrekt, jedoch enthielt er Lücken, die erst mit den Methoden der Analysis des 19. Jahrhunderts geschlossen werden konnten. Eine vereinfachte und auch nach modernen Kriterien noch korrekte Version dieses Beweises wurde von Jean-Robert Argand 1806 angegeben. Weitere veröffentlichte Beweisversuche stammen von Euler (1749), Joseph-Louis Lagrange (1772), aufbauend auf dem Beweis von Euler, und Pierre Simon de Laplace (1795), der einen neuen Ansatz verfolgte unter Verwendung der Diskriminante des Polynoms.

Der erste vollständige Beweis für den Fundamentalsatz der Algebra wurde 1799 von Carl Friedrich Gauß im Rahmen seiner Dissertation angegeben (und eine Notiz dazu in seinem Tagebuch schon im Oktober 1797 eingetragen). Im Gegensatz zu seinen Vorgängern ging Gauß auch das Problem an, die Existenz der Wurzeln im Komplexen zu beweisen, und nicht stillschweigend vorauszusetzen. Auch dieser Beweis enthält einige analytische Schwächen, die erst später beseitigt werden konnten. Der zweite Beweis, der von Gauß 1815 vorgestellt, und ein Jahr später publiziert wurde, baut auf Ideen von Leonhard Euler auf. Dieser Beweis benutzt als analytische Grundlage, unbewiesen und ohne dass eine Beweisnotwendigkeit gesehen wurde, lediglich den Zwischenwertsatz der reellen Analysis, genauer den Spezialfall, dass jedes Polynom ungeraden Grades immer eine reelle Nullstelle hat.

Ein Beweis, der gleichzeitig ein effizientes Berechnungsverfahren beinhaltet, wurde 1859 (und nochmals 1891) von Karl Weierstraß veröffentlicht. Das darin enthaltene Verfahren wird heute als Durand-Kerner-Verfahren bezeichnet.

Inzwischen kennt man mehrere sehr unterschiedliche Beweise, die Begriffe und Ideen aus Analysis, Algebra oder Topologie beinhalten. Am kürzesten kann der Fundamentalsatz der Algebra nach Augustin-Louis Cauchy und Joseph Liouville mit Methoden der Funktionentheorie bewiesen werden. Eine annähernd direkte Plausibilität vermittelt die topologische Argumentation auf Basis der Umlaufzahl. Relativ elementar ist der analytische Beweis.

Im Folgenden sei $f(z)=a_{n}z^{n}+\dotsb +a_{1}z+a_{0}$ stets ein nichtkonstantes Polynom mit komplexen Koeffizienten und insbesondere $a_0,a_n\ne0$ . Dieses sei als Funktion $f\colon \mathbb {C} \to \mathbb {C}$ aufgefasst.

Rein analytischer Beweis

Dieser Beweis wurde 1746 von Jean-Baptiste le Rond d’Alembert vorgeschlagen, jedoch erst 1806 von Jean-Robert Argand vervollständigt. Die zentrale Aussage dieses Beweises ist, dass zu jedem Punkt $z\in \mathbb {C}$ , der keine Nullstelle ist, ein Punkt z+w in der Umgebung angegeben werden kann, der eine Verkleinerung im Betrag des Funktionswerts ergibt, |f(z+w)|<|f(z)| . Hat der Betrag der Funktionswerte also einen Minimalpunkt, so muss dieser ein Nullpunkt sein. Da die Menge $\{z\in \mathbb {C} \mid |f(z)|\leq |f(0)|\}$ kompakt ist, und der Betrag verknüpft mit stetig, gibt es immer einen solchen Minimalpunkt und damit eine Nullstelle.^{[Anm
1]}

Zur zentralen Aussage entwickle man in , d.h.,

$f(z+w)=b_{0}+b_{1}w+\dotsb +b_{n}w^{n}$ .

Ist b_0=0 , so ist eine Nullstelle. Sonst wähle man das kleinste k>0 mit $b_k\ne 0$ und betrachte die beiden Ungleichungen für $s\ge 0$

$|b_0|\ge |b_k|\,s^k$ und $|b_{k}|/2\geq |b_{k+1}|\,s+\dotsb +|b_{n}|\,s^{n-k}$ .

Beide Ungleichungen sind für s=0 erfüllt, und es gibt ein endliches, größtes $\bar s$ , so dass sie auf dem gesamten Intervall $s\in[0,\bar s]$ erfüllt sind. Für ein aus diesem Intervall wähle man ein $w\in \mathbb {C}$ mit |w|=s und so, dass mit einem reellen Faktor $1\ge c>0$ die Beziehung $b_kw^k=-c\,b_0$ gilt. Für den interessierenden Betrag des Funktionswertes gilt nun nach Dreiecksungleichung

$\begin{align} |f(z+w)|\le&|b_0+b_kw^k|+\sum_{j>k}|b_j|\,|w|^j& =&(1-c)|b_0|+\sum_{j>k}|b_j|\,s^j\\[.3em] =&|b_0|-s^k\left(|b_k|-\sum_{j>k}|b_j|\,s^{j-k}\right)& \le& |f(z)|-\tfrac12\,|b_k|\,s^k \end{align}$ .

Beweis mit Methoden der Topologie

Ein Beweis mit dieser Methode wurde 1799 von Gauß gegeben. Er zerlegte die Polynomfunktion in Real- und Imaginärteil, $f(x+\text{i}y)=u(x,y)+\text{i}v(x,y)$ . Die Nullstellenmengen von und sind aus einzelnen eindimensionalen Bögen zusammengesetzt, die eine endliche Anzahl von Knotenpunkten in der Ebene verbinden. Von jedem Knotenpunkt geht eine gerade Anzahl von Bögen aus. Auf keinen Fall kann ein Bogen in einem Punkt einfach enden. Auf jedem Kreis mit genügend großem Radius gibt es Nullstellen von und Nullstellen von , die sich abwechseln. Jeder zusammenhängende Teil des Nullstellengraphen von hat auf einem großen Kreis eine gerade Anzahl von Schnittstellen, die eine ungerade Anzahl von Schnittstellen des Nullstellengraphen von einschließen. Damit muss ein Bogen des Graphen von aus dem zusammenhängenden Teilstück des Graphen von herausragen. Dies geht nur, wenn die Graphen von und sich schneiden, der Schnittpunkt aber ist eine Nullstelle von f(z) .

Zum Polynom $z^{3}+2z^{2}-z+1$ ist das Bild des Kreises mit Radius 10 um den Ursprung dargestellt. Bei großen Kreisen ist die dreifache Umrundung des Ursprungs für alle kubischen Polynome mittels Betragsabschätzung elementar nachweisbar. Wird der Kreis bis zum Nullpunkt verkleinert, zieht sich das Bild auf einen Punkt zusammen, entsprechend dem konstanten Term $a_{0}=1$ .

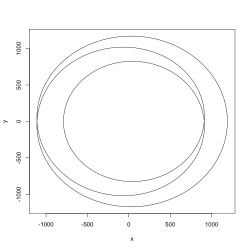
Moderne Versionen dieses Beweises benutzen den Begriff der Windungszahl. Die darauf aufbauende Argumentation liefert zugleich eine direkte Plausibilität für die Richtigkeit des Fundamentalsatzes der Algebra. Siehe dazu auch die Abbildung.

Für den Beweis wird angenommen, dass das Polynom f(z) keine komplexen Nullstellen besitze. Dann kann für jedes s>0 eine geschlossene, stetige Kurve

$\gamma _{s}\colon [0,2\pi ]\to \mathbb {C}$ , $\gamma_s(t)=\min(1,s)^{-n}\,f(s\,e^{\text{i}t})$

konstruiert werden, die die (skalierten) Funktionswerte des Polynoms auf dem Kreis mit Radius durchläuft. Da kein Funktionswert Null ist, kann eine Umlaufzahl definiert werden. Da sich die Kurve bei Änderung des Parameters stetig ändert, kann sich die Umlaufzahl nur ändern, wenn die sich ändernde Kurve den Nullpunkt überquert. Da nach Annahme die Funktion f(z) keine Nullstelle besitzt, ist eine solche Überquerung des Nullpunktes nicht möglich. Daher muss die Umlaufzahl für alle s>0 dieselbe sein.

Für sehr große Werte von wird die Kurve der entsprechenden Kurve der -ten Potenz, genauer des Polynoms a_nz^n , immer ähnlicher, die Umlaufzahl muss daher konstant sein. Für sehr kleine Werte von wird die Kurve der konstanten Kurve mit Wert $a_{0}$ immer ähnlicher, also muss die – für alle s>0 konstante – Umlaufzahl gleichzeitig den Wert 0 besitzen. Dies ist gleichzeitig nur möglich, wenn n = 0 gilt, das Polynom also konstant ist. Für Polynome höheren Grades führt dieses Argument zum Widerspruch, also muss es Nullstellen mit f(z)=0 geben.

Beweis mit dem Zwischenwertsatz und algebraischen Methoden

Ein solcher Beweis wurde 1815 von Gauß präsentiert. Es wird benutzt, dass nach dem Zwischenwertsatz jedes reelle Polynom ungeraden Grades mindestens eine Nullstelle hat, sowie dass quadratische Gleichungen, auch mit komplexen Koeffizienten, elementar lösbar sind. Der Beweis erfolgt als vollständige Induktion über die Potenz des Faktors im Grad des Polynoms.

Es sei zunächst f(z) quadratfrei und mit reellen Koeffizienten vorausgesetzt. Der Grad habe eine Faktorisierung $n=k\,2^m$ mit ungerade. Der Beweis erfolgt als vollständige Induktion über die Potenz des Faktors im Grad des Polynoms. Ist m = 0 , so gibt es eine Nullstelle nach dem Zwischenwertsatz. Es sei nun im Induktionsschritt vorausgesetzt, dass alle Polynome mit Graden $k'\,2^{m-1}$ mit ungerade mindestens eine Nullstelle besitzen.

Es sei, der Einfachheit halber, ein (abstrakter) Zerfällungskörper $\mathbb K\supset \R$ des Polynoms f(z) konstruiert, in welchem es die paarweise verschiedenen (wiederum abstrakten) Nullstellen $z_{1},\dotsc ,z_{n}$ hat,

$f(z)=(z-z_{1})(z-z_{2})\dotsm (z-z_{n})$ .

In $\mathbb K\times \mathbb K$ sei die Menge der $\tfrac12 n(n-1)$ Punkte $(z_j+z_k,z_j\,z_k)$ , j<k , betrachtet. Da die abstrakten Nullstellen paarweise verschieden sind, gibt es nur eine endliche Anzahl von Geraden, die durch mindestens zwei dieser Punkte verlaufen, insbesondere auch nur eine endliche Anzahl reeller Anstiege solcher Geraden, für welche die Differenz $z_j\,z_k-m\,(z_j+z_k)$ zweimal denselben Wert annimmt. Für alle anderen Werte von ist das Polynom

$g_m(x)=\prod_{j<k}(x-m\,(z_j+z_k)+z_j\,z_k)$

ebenfalls quadratfrei und symmetrisch in den abstrakten Nullstellen $z_{1},\dotsc ,z_{n}$ . Daher können die Koeffizienten von g_m(x) als Polynome in und den Koeffizienten von f(z) dargestellt werden, g_m(x) ist also für jedes reelle ein Polynom mit reellen Koeffizienten und kann mittels Resultanten aus f(z) bestimmt werden. Der Grad von g_m(x) beträgt $2^{{m-1}}\,k(n-1)$ , wobei $k(n-1)$ eine ungerade Zahl ist. Nach Induktionsvoraussetzung gibt es wenigstens eine komplexe Nullstelle mit g_m(x)=0 . Aus den partiellen Ableitungen nach und in der Nullstelle können komplexe Zahlen und bestimmt werden, so dass mindestens eine der Nullstellen von $z^2+p\,z+q=0$ eine Nullstelle von f(z) ist.

Hat f(z) auch echt komplexe Koeffizienten, so hat $\tilde f(z)=\bar f(z)\,f(z)$ nur reelle Koeffizienten. Jede Nullstelle des Produkts ist Nullstelle eines Faktors, somit also selbst oder als komplex konjugierte Zahl eine Nullstelle von f(z) . Ist das nun reelle Polynom nicht quadratfrei, so kann mit Polynomarithmetik (u.a. euklidischer Algorithmus) eine Faktorisierung in (nichtkonstante) quadratfreie Faktoren gefunden werden, von denen jeder mindestens eine Nullstelle enthält.

Beweis mit Methoden der Funktionentheorie

Beweis mit dem Satz von Liouville

Wegen $\textstyle\lim_{s\to\infty}\inf_{|z|=s}\left| f(z)\right| =\infty$ existiert ein R>0 , so dass $\left| f(0) \right| \leq \left| f(z) \right|$ für alle $z\in \mathbb {C}$ mit |z|>R gilt. Weil sowohl und damit auch der Betrag |f| stetig sind, als auch die Kreisscheibe $\overline{U_R(0)}$ kompakt ist, existiert nach dem Satz von Weierstrass eine Stelle $z_0\in\overline{U_R(0)}$ mit minimalem Betrag des Funktionswertes, $C:=\left| f(z_0) \right| \leq \left| f(z) \right|$ für alle $z\in\overline{U_R(0)}$ . Nach Konstruktion ist $C=\left| f(z_0) \right|$ sogar ein globales Minimum. Wäre positiv, so wäre die reziproke Funktion $z\mapsto\tfrac{1}{f(z)}$ holomorph auf $\mathbb {C}$ und durch $\tfrac{1}{C}$ beschränkt, also nach dem Satz von Liouville konstant. Somit wäre auch f(z) konstant, was der Voraussetzung widerspricht. Da $C\geq 0$ folgt $C=\left|f(z_{0})\right|=0$ , also existiert eine Nullstelle (in $z_{0}$ ).

Beweis direkt mittels des Cauchyschen Integralsatzes

Der Fundamentalsatz der Algebra ist mit Hilfe elementarer Abschätzungen sogar direkt aus dem Cauchyschen Integralsatz ableitbar, und zwar wie folgt:

Das Polynom lässt sich in der Form $f(z) = z \cdot g(z) + a_0$ darstellen, wobei ein weiteres Polynom ist.

Nimmt man nun an, f(z) sei ohne Nullstelle, so lässt sich für $z\in \mathbb {C} \setminus \{0\}$ stets schreiben:

$\tfrac{1}{z} = \tfrac{f(z)}{ z \cdot f(z) } = \tfrac{g(z)}{f(z)} + \tfrac{a_0}{ z \cdot f(z) }$ .

Nun bildet man für jedes $R \in \N$ das Wegintegral der auf $\mathbb {C} \setminus \{0\}$ gebildeten Kehrwertfunktion $z\mapsto {\tfrac {1}{z}}$ über den Kreislinienweg ${\gamma_R} (t)= R \cdot \exp (i \cdot t ) (t \in [0, 2 \pi ] )$ und erhält:

$2 \pi i = \int\limits_{\gamma_R}\tfrac{1}{z} \,\mathrm dz = \int\limits_{\gamma_R} \tfrac{g(z)}{f(z)} \,\mathrm dz + a_0 \cdot \int\limits_{\gamma_R} \tfrac{1}{ z \cdot f(z) } \,\mathrm dz$ .

Aufgrund der angenommenen Nullstellenfreiheit von f(z) ist

$z \mapsto\tfrac{g(z)}{f(z)}$

holomorph, womit sich infolge des Cauchyschen Integralsatzes weiter ergibt:

$2 \pi i = 0 + a_0 \cdot \int\limits_{\gamma_R} \tfrac{1}{ z \cdot f(z) } \,\mathrm dz$

und daraus:

$2 \pi \leq |a_0| \cdot \operatorname{L}({\gamma_R}) \cdot \max_{|z| = R } \tfrac{1}{ |z \cdot f(z)| } = |a_0| \cdot 2 \pi R \cdot \max_{|z| = R } \tfrac{1}{ |z | \cdot |f(z)| } = |a_0| \cdot 2 \pi \cdot \max_{|z| = R } \tfrac{1}{ |f(z)| }$ .

Dies gilt für jedes beliebige $R\in \mathbb {R} ^{>0}$ .

Nun ist jedoch $\textstyle\lim_{|z| \to \infty}\ | f(z)| = \infty$ und damit folgt aus der letzten Ungleichung unmittelbar:

$2 \pi \leq 0$ ,

was sicher falsch ist.

Damit ist die angenommene Nullstellenfreiheit von f(z) zum Widerspruch geführt und f(z) muss eine Nullstelle haben.

Beweisvariante mittels des Cauchyschen Integralsatzes

Eine Beweisvariante unter Verwendung des Cauchyschen Integralsatzes findet sich bei Bartel Leendert van der Waerden:

Unter der Annahme, dass $f(z)\neq 0\;\forall z\in \mathbb {C}$ für die Polynomfunktion gelte, setze $\phi (z):={\frac {1}{f(z)}}$ und betrachte $\psi \colon \mathbb {C} \to \mathbb {C}$ definiert durch $\psi (z):={\frac {\phi (z)-\phi (0)}{z}}$ für $z\neq 0$ und stetig fortgesetzt bei z=0 dank $\lim _{z\to 0}\psi (z)={\frac {\mathrm {d} \phi }{\mathrm {d} z}}(0)$ . Mit sind – gemäß Annahme – auch $\phi$ und $\psi$ auf der gesamten Ebene $\mathbb {C}$ holomorph, das heißt ganze Funktionen. Also verschwindet nach dem Cauchyschen Integralsatz das Weg-Integral über eine Kreislinie $\mathrm {K} =\mathrm {K} (R)$ mit Radius um den Nullpunkt, und mittels Kreislinienparametrisierung^{[Anm
2]} kommt:

$0=\oint _{\mathrm {K} }\psi (z)\;\mathrm {d} z=\int _{0}^{2\pi }\phi (Re^{i\theta })\,i\;\mathrm {d} \theta -\underbrace {\int _{0}^{2\pi }\phi (0)\,i\;\mathrm {d} \theta } _{=2\pi i\,\phi (0)}$

Nun gibt es zu jedem beliebig gegebenem $\epsilon >0$ einen genügend großen Radius , so dass für den Integranden $|\phi (Re^{i\theta })|<\epsilon$ auf $\mathrm{K}$ gilt, und für das Integral folglich $\left|2\pi i\,\phi (0)\right|=\left|\int _{0}^{2\pi }\phi (Re^{i\theta })\,i\;\mathrm {d} \theta \right|<2\pi \epsilon$ . Hieraus folgt $\phi (0)=0$ , was auf den Widerspruch $1{\stackrel {{\text{Def }}\phi }{=}}f(0)\,\phi (0)=0$ stößt.

Beweis mit Methoden der komplexen Geometrie

Wir fassen f(z) als Abbildung des komplex-projektiven Raums $\mathbb {P} _{\mathbb {C} }^{1}\to \mathbb {P} _{\mathbb {C} }^{1}$ auf, d.h. $z\in \mathbb {C} \mapsto f(z)\in \mathbb {C}$ , $\infty \mapsto \infty$ . Die so definierte Abbildung komplexer Mannigfaltigkeiten ist holomorph und damit offen (d.h. das Bild jeder offenen Teilmenge ist offen). Da $\mathbb {P} _{\mathbb {C} }^{1}$ kompakt und stetig ist, ist das Bild $f(\mathbb {P} _{\mathbb {C} }^{1})$ auch kompakt, insbesondere abgeschlossen in $\mathbb {P} _{\mathbb {C} }^{1}$ . Damit ist das Bild bereits ganz $\mathbb {P} _{\mathbb {C} }^{1}$ , denn $\mathbb {P} _{\mathbb {C} }^{1}$ ist zusammenhängend. Insbesondere gibt es ein $z\in \mathbb {C}$ , welches auf $0$ abgebildet wird, d.h. eine Nullstelle von .

Beweis mit Methoden der Differentialtopologie

Ähnlich wie im obigen Beweis aus der komplexen Geometrie fassen wir als Selbstabbildung der Sphäre $\mathbb S^2$ auf. So ist $f\colon\mathbb S^2\to\mathbb S^2$ (reell) differenzierbar und die Menge der kritischen Punkte ist als Nullstellenmenge der Ableitung endlich, womit die Menge der regulären Werte zusammenhängend ist. Die Kardinalität $|f^{-1}(y)|$ des Urbilds eines regulären Wertes $y\in\mathbb S^2$ ist außerdem lokal konstant als Funktion in ( ist injektiv auf Umgebungen von Punkten in $f^{-1}(y)$ ). Dies zeigt, dass surjektiv ist, denn reguläre Werte werden somit stets angenommen und kritische Werte werden nach Definition angenommen.

Verallgemeinerung des Fundamentalsatzes

Der Fundamentalsatz der Algebra lässt sich mit Hilfe topologischer Methoden unter Anwendung der Homotopietheorie und des Abbildungsgrades weiter verallgemeinern:

Jede stetige Funktion $f\colon \mathbb {C} \to \mathbb {C}$ , für die eine natürliche Zahl und weiter eine komplexe Zahl $c \neq 0$ existieren derart, dass $\textstyle\lim_{z \to \infty}\ \tfrac{f(z)}{ z ^n} = c$ erfüllt ist, hat eine Nullstelle.

Hieraus folgt der Fundamentalsatz, indem man zu einer komplexen Polynomfunktion $z \mapsto f(z)=a_n z^n + a_{n-1} z^{n-1} + \dotsb + a_1 z + a_0$ $(z\in \mathbb {C} )$ vom Grad n > 0 den Leitkoeffizienten als Konstante, also c = a_n nimmt.

Literatur

Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 3., neu bearbeitete und erweiterte Auflage. Springer-Verlag, Berlin u.a. 2000, ISBN 3-540-67641-4.
Egbert Harzheim: Einführung in die Kombinatorische Topologie (= Die Mathematik. Einführungen in Gegenstand und Ergebnisse ihrer Teilgebiete und Nachbarwissenschaften). Wissenschaftliche Buchgesellschaft, Darmstadt 1978, ISBN 3-534-07016-X.
Reinhold Remmert: Fundamentalsatz der Algebra, in D. Ebbinghaus u.a. (Hrsg.), Zahlen, Springer, 1983.
Bartel Leendert van der Waerden: Algebra I, unter Benutzung von Vorlesungen von E. Artin und E. Noether. 2.–6. Auflage (der Modernen Algebra) (1930 bis 1964), Springer-Verlag. In der 8. Auflage, 1971, Heidelberger Taschenbücher Band 12, ISBN 3-540-03561-3,

Anmerkungen

↑ Man beachte hier den Satz von Bolzano-Weierstraß oder Folgerungen daraus.
↑ Nämlich $[0,2\pi ]\to \mathrm {K} ,\,\theta \mapsto z:=Re^{i\theta }$ mit $\mathrm {d} z=zi\,\mathrm {d} \theta$

Basierend auf einem Artikel in:

Wikipedia.de