
Kurvenintegral
Das Kurven-, Linien-, Weg- oder Konturintegral erweitert den gewöhnlichen Integralbegriff für die Integration in der komplexen Ebene (Funktionentheorie) oder im mehrdimensionalen Raum (Vektoranalysis).
Den Weg, die Linie oder die Kurve, über die integriert wird, nennt man den Integrationsweg.
Wegintegrale über geschlossene
Kurven werden auch als Ringintegral, Umlaufintegral
oder Zirkulation bezeichnet und mit dem Symbol
geschrieben.
Reelle Wegintegrale
Wegintegral erster Art
Das Wegintegral einer stetigen Funktion,
entlang eines stückweise stetig differenzierbaren Weges
ist definiert als
Dabei bezeichnet
die Ableitung von
nach
und
die euklidische
Norm des Vektors
.
Die Bildmenge
ist eine stückweise glatte Kurve in
.
Anmerkungen
- Ein Beispiel für eine solche Funktion
ist ein Skalarfeld mit kartesischen Koordinaten.
- Ein Weg
kann eine Kurve
entweder als Ganzes oder auch nur in Abschnitten mehrfach durchlaufen.
- Für
ergibt das Wegintegral erster Art die Länge des Weges
.
- Der Weg
bildet u.a.
auf den Anfangspunkt der Kurve ab und
auf deren Endpunkt.
ist ein Element der Definitionsmenge von
und steht allgemein nicht für die Zeit.
ist das zugehörige Differential.
Wegintegral zweiter Art

Das Wegintegral über ein stetiges Vektorfeld
mit einer ebenfalls so parametrisierten Kurve ist definiert als das Integral
über das Skalarprodukt
aus
und
:
Einfluss der Parametrisierung
Sind
und
einfache (d. h.
und >
sind injektiv)
Wege mit
und
und demselben Bild,
parametrisieren sie also dieselbe Kurve in derselben Richtung und durchlaufen
sie die Kurve (bis auf Doppelpunkte) genau einmal, so stimmen die Integrale
entlang
und
überein. Dies rechtfertigt den Namen Kurvenintegral; ist die
Integrationsrichtung aus dem Kontext ersichtlich oder irrelevant, wird daher der
Weg in der Notation unterdrückt.
Kurvenintegrale
Da eine Kurve
das Bild eines Weges
ist, entsprechen die Definitionen der Kurvenintegrale im Wesentlichen den
Wegintegralen.
Kurvenintegral 1. Art:
Kurvenintegral 2. Art:
Ein Spezialfall ist wieder die Länge der durch
parametrisierten Kurve
:
Wegelement und Längenelement
Der in den Kurvenintegralen erster Art auftretende Ausdruck
heißt skalares Wegelement oder Längenelement. Der in den Kurvenintegralen zweiter Art auftretende Ausdruck
heißt vektorielles Wegelement.
Rechenregeln
Seien ,
Kurvenintegrale gleicher Art (d. h. entweder beide erster oder beide zweiter
Art), sei das Urbild der beiden Funktionen
und
von gleicher Dimension und sei
.
Dann gelten für
,
und
die folgenden Rechenregeln:
(Linearität)
(Zerlegungsadditivität)
Notation für Kurvenintegrale von geschlossenen Kurven
Ist
ein geschlossener Weg, so schreibt man
- statt
auch
,
und analog für geschlossene Kurven
- statt
auch
.
Mit dem Kreis im Integral möchte man deutlich machen, dass
geschlossen ist. Der einzige Unterschied liegt hierbei in der Notation.
Beispiele
- Ist
der Graph einer Funktion
, so wird diese Kurve durch den Weg
-
- parametrisiert. Wegen
- ist die Länge der Kurve gleich
- Eine Ellipse mit großer Halbachse
und kleiner Halbachse
wird durch
für
parametrisiert. Ihr Umfang ist also
-
.
- Dabei bezeichnet
die numerische Exzentrizität
der Ellipse. Das Integral auf der rechten Seite wird aufgrund dieses Zusammenhanges als elliptisches Integral bezeichnet.
Wegunabhängigkeit
Ist ein Vektorfeld
ein Gradientenfeld,
d.h.
ist der Gradient
eines skalaren Feldes
,
mit
so gilt für die Ableitung
der Verkettung
von
und
was gerade dem Integranden des Wegintegrals über
auf
entspricht. Daraus folgt für eine gegebene Kurve
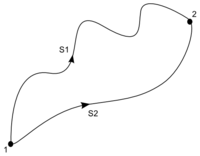
Dies bedeutet, dass das Integral von
über
ausschließlich von den Punkten
und
abhängt und der Weg dazwischen irrelevant für das Ergebnis ist. Aus diesem Grund
wird das Integral eines Gradientenfeldes als "wegunabhängig" bezeichnet.
Insbesondere gilt für das Ringintegral über die geschlossene Kurve ,
mit zwei beliebigen Wegen
und
Dies ist insbesondere in der Physik
von großer Bedeutung, da beispielsweise die Gravitation
diese Eigenschaften besitzt. Da die Energie in diesen Kraftfeldern stets eine
Erhaltungsgröße ist, werden sie in der Physik als konservative
Kraftfelder bezeichnet. Das skalare Feld
ist dabei das Potential
beziehungsweise die potentielle
Energie. Konservative Kraftfelder erhalten die mechanische Energie,
d.i. die Summe aus kinetischer
Energie und potentieller Energie. Gemäß dem obigen Integral wird auf einer
geschlossenen Kurve insgesamt eine Arbeit von 0 J aufgebracht.
Wegunabhängigkeit lässt sich auch mit Hilfe der Integrabilitätsbedingung zeigen.
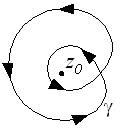
Ist das Vektorfeld nur in einer (kleinen) Umgebung
eines Punktes nicht als Gradientenfeld darstellbar, so ist das geschlossene
Wegintegral von Kurven außerhalb von
proportional zur Windungszahl um diesen Punkt und ansonsten unabhängig vom
genauen Verlauf der Kurve (siehe Algebraische
Topologie: Methodik).
Komplexe Wegintegrale
Ist
eine komplexwertige
Funktion, dann nennt man
integrierbar, wenn
und
integrierbar sind. Man definiert
.
Das Integral ist damit -linear.
Ist
im Intervall
stetig und
eine Stammfunktion von
,
so gilt wie im Reellen
.
Der Integralbegriff wird nun auf die komplexe Ebene wie folgt erweitert: Ist
eine komplexwertige Funktion auf einem Gebiet
,
und ist
ein stückweise stetig differenzierbarer Weg
in
,
so ist das Wegintegral von
entlang des Weges
definiert als
Der Malpunkt bezeichnet hier komplexe Multiplikation.
Die zentrale Aussage über Wegintegrale komplexer Funktionen ist der Cauchysche
Integralsatz: Für eine holomorphe
Funktion
hängt das Wegintegral nur von der Homotopieklasse
von
ab. Ist
einfach
zusammenhängend, so hängt das Integral also überhaupt nicht von
,
sondern nur von Anfangs- und Endpunkt ab.
Analog zum reellen Fall definiert man die Länge des Weges
durch
.
Für theoretische Zwecke ist folgende Ungleichung, die sogenannte Standardabschätzung, von besonderem Interesse:
, wenn
für alle
gilt.
Wie im reellen Fall ist das Wegintegral unabhängig von der Parametrisierung
des Weges ,
d. h. es ist nicht zwingend notwendig,
als Parameterbereich zu wählen, wie sich durch Substitution zeigen lässt. Dies
erlaubt die Definition komplexer Kurvenintegrale, indem man den obigen Formeln
den Weg
durch eine Kurve
in
ersetzt.
Siehe dagegen
Literatur
- Harro Heuser: Lehrbuch der Analysis – Teil 2. 1981; 5. Auflage, Teubner 1990, ISBN 3-519-42222-0.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 10.06. 2021