Konforme Abbildung

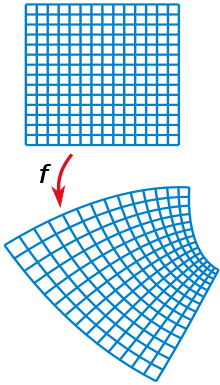
Abb. 1: Ein rechtwinkliges Netz (oben) und sein Bild (unten) nach einer konformen Abbildung . Linienpaare, die sich unter 90° schneiden, werden abgebildet auf Linienpaare, die sich auch unter 90° schneiden.

Eine konforme Abbildung ist eine winkeltreue Abbildung.

Das bedeutet u. a., dass aus einem rechtwinkligen Koordinatennetz durch eine konforme Abbildung zwar ein i.Allg. krummliniges Koordinatennetz entsteht, dass aber „im Kleinen“ die rechtwinklige Netzstruktur vollständig erhalten bleibt, also insbesondere die Zwischenwinkel und die Längenverhältnisse je zweier beliebiger Vektoren.

Solche Abbildungen finden vielfache Anwendungen in der theoretischen Physik, u.a. in der Theorie komplizierter elektrostatischer Potentiale und der zugehörigen elektrostatischen Felder sowie in der Strömungsmechanik.

Definition

Eine lineare Abbildung $L\colon \mathbb {R} ^{m}\to \mathbb {R} ^{n}$ heißt konform, wenn ${\frac {\langle Lv,Lw\rangle }{\|Lv\|_{2}\|Lw\|_{2}}}={\frac {\langle v,w\rangle }{\|v\|_{2}\|w\|_{2}}}$ für alle $v,w\in \mathbb {R} ^{m}$ gilt. Hierbei ist $\langle \cdot ,\cdot \rangle$ das Standardskalarprodukt und $\| \cdot \|_2$ die euklidische Norm.

Des Weiteren heißt eine differenzierbare Abbildung konform in , wenn ihr Differential in konform ist.

Eigenschaften

Falls eine offene Teilmenge der komplexen Ebene $\mathbb {C}$ ist, dann ist die Funktion $f\colon U\to \mathbb {C}$ konform genau dann, wenn sie holomorph oder anti-holomorph ist und ihre Ableitung ungleich null auf ganz ist. Die konformen Abbildungen bilden also die geometrische Veranschaulichung der komplex differenzierbaren (analytischen oder holomorphen) Funktionen einer komplexen Variablen (vgl. die Veranschaulichung reeller Funktionen durch ebene Kurven). Real- bzw. Imaginärteil einer solchen Funktion bzw. ihrer lokal rechtwinkligen Koordinatennetze können z.B. als Potentiale eines elektrostatischen Feldes oder eines Strömungsfeldes interpretiert werden. Auch meromorphe Funktionen sind nützlich, weil deren Polstellen die Dipole, Quadrupole usw., allgemein: die Multipole dieser Potentiale erzeugen.

Die konformen Abbildungen des Minkowski-Raums auf sich selbst umfassen die Lorentz-Transformationen und Translationen, die die Metrik unverändert lassen, die Dilatationen, die die Metrik um eine glatte Funktion skalieren sowie die speziellen konformen Transformationen, zu denen die Inversion an einer Kugeloberfläche gehört.

Wie die Lorentz-Transformationen und die Poincaré-Transformationen bilden auch die konformen Transformationen eine Lie-Gruppe, die konforme Gruppe.

Physikalische Anwendungen

Abb. 2: Tragflügel und Kreis hängen durch eine konforme Abbildung zusammen.

Die nebenstehende Abbildung 2 zeigt an einem Beispiel aus dem „Flugzeugbau“, dass durch die konforme Abbildung komplizierte Kurven auf wesentlich einfachere abgebildet werden können. Das abgebildete Beispiel einer konformen Abbildung ist die Joukowski-Funktion (auch „Schukowski-Funktion“ geschrieben). Bei dieser Abbildung wird das Joukowski-Profil auf einen Kreis abgebildet. Die Geschwindigkeit, mit der etwa Luftteilchen das (zweidimensionale) Tragflügel-Profil umströmen, wird einfacher berechenbar, wenn es um die Umströmung eines Kreiszylinders geht. Damit wird plausibel, dass die konformen Abbildungen in folgenden Gebieten eine wichtige Bedeutung haben, solange man Phänomene in der zweidimensionalen Ebene untersucht:

Strömungslehre (Aerodynamik, Hydrodynamik)
Elektrostatik (vgl. das elektrostatische Feld in Analogie zu Strömungsfeldern)
Wärmeleitung

Invarianz unter konformen Abbildungen

Im Falle des -dimensionalen Minkowski-Raumes gilt: Die Zusammenhangskomponente der 1 von der Gruppe der orientierungstreuen konformen Transformationen ist isomorph zur Gruppe SO(d,2) , wenn $d>2$ gilt. Für d=2 ist diese Gruppe unendlichdimensional. Sie ist isomorph zu ${\mathrm {Diff}}_{+}({\mathbb R})\times {\mathrm {Diff}}_{+}({\mathbb R})$ , wobei ${\mathrm {Diff}}_{+}({\mathbb R})$ die unendlichdimensionale Gruppe der orientierungstreuen Diffeomorphismen von $\mathbb {R}$ auf sich bezeichnet.

Im Falle des -dimensionalen euklidischen Raumes ist die entsprechende Gruppe isomorph zu SO(d+1,1) , $d\geq 2$ . Im Falle d=2 ist sie daher auch isomorph zur Gruppe der Möbiustransformationen.

Physikalische Systeme, die unveränderlich unter konformen Abbildungen sind, haben eine große Bedeutung in der Festkörperphysik, in der Stringtheorie und in der konformen Feldtheorie.

Konforme Abbildungen auf (semi-) riemannschen Mannigfaltigkeiten

Seien (M,g) und (N,h) zwei riemannsche Mannigfaltigkeiten bzw. semi-riemannsche Mannigfaltigkeiten. und bezeichnen die metrischen Tensoren. Zwei Metriken und auf einer Mannigfaltigkeit heißen in der riemannschen Geometrie „konform äquivalent“, falls $g=uh$ mit einer auf definierten positiven Funktion , die konformer Faktor genannt wird. Die Klasse konform äquivalenter Metriken auf heißt konforme Struktur.

Ein Diffeomorphismus $f\colon M\to N$ heißt konform, falls $h_{f(x)}(\mathrm {d} f_{x}(v),\mathrm {d} f_{x}(w))=e^{\sigma (x)}\cdot g_{x}(v,w)$ für alle Punkte $x\in M$ und Vektoren $v,w\in T_{{x}}M$ des Tangentialraumes gilt. Man drückt das auch so aus, dass die Pullback-Metrik auf konform äquivalent zur Metrik von ist. Die Potenz $e^{{\sigma (x)}}$ soll andeuten, dass der Faktor stets größer als 0 ist, dass es sich also um einen konformen Faktor handelt. Ein Beispiel einer konformen Abbildung ist die stereographische Projektion der Kugeloberfläche auf die projektive Ebene (Ebene ergänzt durch einen Punkt im Unendlichen).

Die konformen Abbildungen einer Mannigfaltigkeit in sich selbst werden von konformen Killing-Vektorfeldern erzeugt.

Basierend auf einem Artikel in:

Wikipedia.de