Rücktransport

In verschiedenen Teilgebieten der Mathematik bezeichnet man als Pullback oder Rücktransport (auch: Zurückziehung, Rückzug) Konstruktionen, die ausgehend von einer Abbildung $f\colon X\to Y$ und einem Objekt , das in irgendeiner Weise zu gehört, ein entsprechendes, „entlang von zurückgezogenes“ Objekt für liefern; es wird häufig mit $f^{*}E$ bezeichnet.

Das duale Konzept heißt meist Pushforward.

In der Kategorientheorie ist Pullback eine andere Bezeichnung für das Faserprodukt. Das duale Konzept wird hier Pushout, cokartesisches Quadrat oder Fasersumme genannt.

Motivation: Der Rücktransport einer glatten Funktion

Sei $f\colon M\to N$ ein Diffeomorphismus zwischen glatten Mannigfaltigkeiten und sei $\psi \colon N\to \mathbb{R}$ eine glatte Funktion auf . Dann ist der Rücktransport von $\psi$ bezüglich definiert durch

$f^{*}\colon C^{\infty }(N)\to C^{\infty }(M)$ mit $(f^{*}(\psi ))(x)=\psi (f(x))\,.$

Der Rücktransport $f^{*}\psi$ ist also eine glatte Funktion $M\to \mathbb{R}$ .

Schränkt man die Funktion $\psi$ auf eine offene Teilmenge $U\subset N$ ein, so erhält man ebenso eine glatte Funktion auf $f^{{-1}}(U)\subset M$ . Der Rücktransport ist also ein Morphismus zwischen den Garben der glatten Funktionen von und .

Der Rücktransport eines Vektorbündels

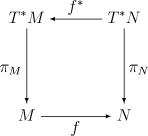
Schema eines Pull-Back am Beispiel der Kotangentialbündel

Seien und topologische Räume, $\pi \colon E\to N$ ein Vektorbündel über und $f\colon M\to N$ eine stetige Abbildung. Dann ist das zurückgezogene Vektorbündel $\pi _{{E'}}\colon E'\to M$ definiert durch

$E':=\{(x,e)\in M\times E|f(x)=\pi (e)\}$

zusammen mit der Projektion $\pi _{{E'}}(x,e):=x$ . Meist notiert man dieses Vektorbündel mittels $f^{*}E$ und nennt es auch Pullbackbündel von bezüglich .

Ist $\omega \in \Gamma (N,E)$ ein Schnitt im Vektorbündel , so ist $f^{*}\omega \in \Gamma (M,f^{*}E)$ der zurückgezogene Schnitt, der durch

$(f^{*}\omega )_{p}=\omega _{{f(p)}}$

für alle $p\in M$ gegeben ist.

Das zurückgezogene Vektorbündel ist ein Spezialfall eines Faserproduktes. Im Bereich der Differentialgeometrie werden meist glatte Mannigfaltigkeiten anstatt beliebiger topologischer Räume und betrachtet. Dann wird auch zusätzlich gefordert, dass die Abbildung $f\colon M\to N$ und das Vektorbündel differenzierbar sind.

Dualer Operator

Seien $\pi _{E}\colon E\to N$ und $\pi _{F}\colon F\to M$ zwei Vektorbündel und $\phi \colon M\to N$ eine stetige Abbildung, so dass $\phi ^{*}\colon E\to F$ der entsprechende Rücktransport ist. Der duale Operator des Rücktransports ist der Pushforward $\phi _{*}\colon F\to E$ von $\phi$ .

Schema eines Pushforward, TN ist das Tangentialbündel zur Mannigfaltigkeit N

Rücktransport bestimmter Objekte

In diesem Abschnitt sind und glatte Mannigfaltigkeiten und sei $f\colon M\to N$ eine glatte Abbildung.

Glatte Funktionen

Die Menge $C^\infty(M)$ der glatten Funktionen $\psi \colon N\to \mathbb{R}$ kann auf natürliche Weise mit dem Vektorraum $\Gamma ^{\infty }(M,M\times \mathbb{R} )$ der glatten Schnitte im Vektorbündel $\textstyle \coprod _{{p\in M}}\mathbb{R} \cong M\times \mathbb{R}$ aufgefasst werden. Entsprechend kann der Rücktransport einer glatten Funktion $(f^{*}(\psi ))(x)=\psi (f(x))$ auch als Rücktransport eines glatten Schnittes des Vektorbündels $M\times \mathbb{R}$ aufgefasst werden.

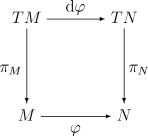
Differentialformen

Da die Menge der Differentialformen ein Vektorbündel bilden, kann man den Rücktransport einer Differentialform untersuchen.

Ist $f\colon M\to N$ eine differenzierbare Abbildung und $\omega \in \Gamma (N,\Lambda ^{k}(T^{*}N))$ eine k-Form auf , so ist die auf zurückgezogene Differentialform $f^*\omega$ , die im Fall von 1-Formen durch

$(f^{*}\omega )_{p}(X)=\omega _{{f(p)}}(f_{{*p}}X)$

für Tangentialvektoren $X\in T_{p}M$ im Punkt $p\in M$ gegeben.

Basierend auf einem Artikel in:

Wikipedia.de