Differenzierbare Mannigfaltigkeit

In der Mathematik sind differenzierbare Mannigfaltigkeiten ein Oberbegriff für Kurven, Flächen und andere geometrische Objekte, die – aus der Sicht der Analysis – lokal aussehen wie ein euklidischer Raum. Im Unterschied zu topologischen Mannigfaltigkeiten ist es auf differenzierbaren Mannigfaltigkeiten möglich, über Ableitungen und verwandte Konzepte zu sprechen. Differenzierbare Mannigfaltigkeiten sind Hauptgegenstand der Differentialgeometrie und der Differentialtopologie. Sie spielen auch eine zentrale Rolle in der theoretischen Physik, insbesondere in der klassischen Mechanik bei Systemen, die Zwangsbedingungen unterliegen, und bei der Beschreibung der Raumzeit in der allgemeinen Relativitätstheorie.

Es gibt zwei Herangehensweisen an differenzierbare Mannigfaltigkeiten:

als Teilmengen eines höherdimensionalen euklidischen Raumes, die entweder durch Gleichungen oder durch Parametrisierungen beschrieben sind und im Artikel Untermannigfaltigkeit des $\mathbb {R} ^{n}$ behandelt werden
als abstrakte Mannigfaltigkeiten, deren differenzierbare Struktur durch einen Atlas gegeben ist.

Die Äquivalenz der beiden Sichtweisen wird durch den Einbettungssatz von Whitney sichergestellt.

Definitionen

Differenzierbarer Atlas

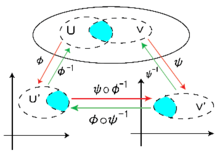
Die Grafik illustriert einen Kartenwechsel der Karten $(U,\phi )$ und $(V,\psi )$ . Der große Kreis symbolisiert den topologischen Raum und die zwei unteren kleineren Kreise symbolisieren Teilmengen des $\mathbb {R} ^{n}$ .

Eine Karte eines topologischen Raums ist ein Paar $(U,\phi )$ bestehend aus einer in offenen, nichtleeren Menge $U\subseteq M$ und einem Homöomorphismus

$\phi \colon \ U\to \phi (U)\subseteq \mathbb {R} ^{n}$ .

Sind $(U,\phi )$ und $(V,\psi )$ zwei Karten von mit $U\cap V\neq \emptyset$ , so nennt man die Abbildung

$\psi \circ \phi ^{-1}\colon \ \phi (U\cap V)\to \psi (U\cap V)$

einen Kartenwechsel.

Ein Atlas für ist dann eine Familie $(U_{i},\phi _{i})_{i\in I}$ von Karten ( ist eine Indexmenge), so dass

$M=\bigcup _{i\in I}U_{i}$

gilt. Man nennt einen Atlas $C^{k}$ -differenzierbar mit $k\geq 1$ , wenn alle seine Kartenwechsel $C^{k}$ -Diffeomorphismen sind.

Differenzierbare Struktur

Zwei $C^{k}$ -differenzierbare Atlanten sind äquivalent, wenn auch ihre Vereinigung ein $C^{k}$ -differenzierbarer Atlas ist. Eine Äquivalenzklasse von Atlanten bezüglich dieser Äquivalenzrelation wird $C^{k}$ -differenzierbare Struktur der Mannigfaltigkeit genannt.

Ist $k=\infty$ , so spricht man auch von einer glatten Struktur.

Differenzierbare Mannigfaltigkeit

Eine -mal differenzierbare Mannigfaltigkeit ist ein topologischer Hausdorffraum, der das zweite Abzählbarkeitsaxiom erfüllt, zusammen mit einer $C^{k}$ -differenzierbaren Struktur.

Die differenzierbare Mannigfaltigkeit hat die Dimension , wenn eine Karte und damit alle Karten in eine Teilmenge des $\mathbb {R} ^{n}$ abbilden.

Glatte Mannigfaltigkeit

Eine glatte Mannigfaltigkeit ist ebenfalls ein topologischer Hausdorffraum, der das zweite Abzählbarkeitsaxiom erfüllt, zusammen mit einer glatten Struktur.

Auf glatten Mannigfaltigkeiten kann man Funktionen auf Glattheit untersuchen, was natürlich bei -mal differenzierbaren Mannigfaltigkeiten nicht möglich ist, da dort eben der Kartenwechsel nur -mal differenzierbar ist und man deshalb jede Funktion auf der Mannigfaltigkeit nur höchstens -mal differenzieren kann. Oftmals betrachten Differentialgeometer nur die glatten Mannigfaltigkeiten, da man für diese etwa dieselben Resultate erhält wie für die -mal differenzierbaren, aber nicht verwalten muss, wie oft man die Kartenwechsel noch differenzieren darf.

Komplexe Mannigfaltigkeit

Komplexe Mannigfaltigkeiten sind ebenfalls glatt, allerdings mit dem Zusatz, dass die Kartenwechsel zusätzlich biholomorph sind.

Beispiele

Die zweidimensionale Sphäre

Der euklidische Vektorraum $\mathbb {R} ^{n}$ kann auch als -dimensionale differenzierbare Mannigfaltigkeit verstanden werden. Einen differenzierbaren Atlas bestehend aus einer Karte erhält man mittels der identischen Abbildung.
Das wahrscheinlich einfachste, aber nichttriviale Beispiel einer differenzierbaren Mannigfaltigkeit ist die -dimensionale Sphäre. Die zweidimensionale Sphäre kann man sich als Hülle einer Kugel vorstellen. Einen differenzierbaren Atlas der Sphäre erhält man schon mit Hilfe von zwei Karten beispielsweise mit Hilfe der stereographischen Projektion. Auf der Sphäre ist es allerdings je nach Dimension möglich, unterschiedliche nicht kompatible differenzierbare Atlanten zu definieren.

Differenzierbare Abbildungen, Wege und Funktionen

Sind eine -dimensionale und eine -dimensionale $C^{k}$ -Mannigfaltigkeit, so nennt man eine stetige Abbildung $F\colon M\to N$ eine $C^{k}$ -Abbildung oder -mal stetig differenzierbar (kurz: differenzierbar), wenn dies für ihre Kartendarstellungen (das sind dann Abbildungen von $\mathbb {R} ^{m}$ nach $\mathbb {R} ^{n}$ ) gilt.

Im Detail: Ist $(U,\phi )$ eine Karte von und $(V,\psi )$ eine Karte von mit $F(U)\subset V$ , so nennt man

$\psi \circ F\circ \phi ^{-1}\colon \phi (U)\to \psi (V)$

eine Kartendarstellung von (bezüglich der beiden Karten).

Die Abbildung heißt nun von der Klasse $C^{k}$ oder -mal stetig differenzierbar, wenn alle Kartendarstellungen von der Klasse $C^{k}$ sind. Die Differenzierbarkeit hängt dabei nicht von der Wahl der Karten ab. Dies ergibt sich daraus, dass die Kartenwechselabbildungen $C^{k}$ -Diffeomorphismen sind, und aus der mehrdimensionalen Kettenregel. Stetigkeit von folgt nicht aus der Differenzierbarkeit, sondern muss vorausgesetzt werden, damit die Karten so gewählt werden können, dass $F(U)\subset V$ gilt.

Abbildungen von der Klasse $C^{\infty }$ , die also beliebig oft differenzierbar sind, werden auch als glatte Abbildungen bezeichnet.

Die Fälle $M=\mathbb {R} ^{m}$ bzw. $N=\mathbb {R} ^{n}$ sind auch möglich. In diesem Fall kann dort auf die Karten verzichtet werden.

Eine differenzierbare Abbildung von einem Intervall $I\subset \mathbb {R}$ in eine Mannigfaltigkeit heißt Weg oder parametrisierte Kurve. Ist der Zielraum $\mathbb {R}$ , so spricht man von einer differenzierbaren Funktion auf .

Eine Abbildung $F\colon M\to N$ heißt lokaler $C^{k}$ -Diffeomorphismus, wenn die Karten so gewählt werden können, dass die Kartendarstellungen von Diffeomorphismen sind. Ist außerdem bijektiv, so nennt man einen $C^{k}$ -Diffeomorphismus.

Um tatsächlich eine Ableitung für Abbildungen zwischen differenzierbaren Mannigfaltigkeiten definieren zu können, braucht man eine zusätzliche Struktur, den Tangentialraum. Für die Definition der Ableitung einer differenzierbaren Abbildung zwischen Mannigfaltigkeiten siehe Tangentialraum und Pushforward.

Eigenschaften

Auf einer zusammenhängenden differenzierbaren Mannigfaltigkeit operiert die Diffeomorphismengruppe transitiv, das heißt für alle $x,y\in M$ gibt es einen Diffeomorphismus $F\colon M\to M$ , sodass gilt.
Die Klasse der $C^{k}$ -Mannigfaltigkeiten bildet zusammen mit der Klasse der $C^{k}$ -Abbildungen eine Kategorie.
Differenzierbare Mannigfaltigkeiten sind triangulierbar was für topologische Mannigfaltigkeiten im Allgemeinen nicht gilt.

Untermannigfaltigkeiten

→ Hauptartikel: Untermannigfaltigkeit

Eine -dimensionale Untermannigfaltigkeit einer -dimensionalen Mannigfaltigkeit ( n<m ) ist eine Teilmenge, die in geeigneten Karten so erscheint wie ein -dimensionaler linearer Unterraum des $\mathbb {R} ^{m}$ . Diese besitzt in kanonischer Weise eine differenzierbare Struktur.

Im Detail: Eine Teilmenge einer -dimensionalen differenzierbaren Mannigfaltigkeit ist eine -dimensionale Untermannigfaltigkeit, falls es zu jedem Punkt $p\in N$ eine Karte $(U,\phi )$ um gibt, so dass

$\phi (N\cap U)=(\mathbb {R} ^{n}\times \{0\})\cap \phi (U).$

Dabei wird der $\mathbb {R} ^{m}$ als $\mathbb {R} ^{n}\times \mathbb {R} ^{m-n}$ aufgefasst; die „0“ auf der rechten Seite ist die 0 von $\mathbb {R} ^{m-n}$ . Solche Karten heißen Schnittkarten. Diese definieren auf auf natürliche Weise eine differenzierbare Struktur, die mit der differenzierbaren Struktur von verträglich ist: Identifiziert man $\mathbb {R} ^{n}\times \{0\}$ mit $\mathbb {R} ^{n}$ , so ist die Einschränkung $(U\cap N,\phi |_{U\cap N})$ der Schnittkarte $(U,\phi )$ auf $U\cap N$ eine Karte von und die Menge aller so erhaltenen Karten bildet einen differenzierbaren Atlas von .

Einbettungssatz von Whitney

→ Hauptartikel: Einbettungssatz von Whitney

Der Einbettungssatz von Whitney besagt, dass es zu jeder -dimensionalen differenzierbaren Mannigfaltigkeit eine Einbettung $M\to \mathbb {R} ^{2n}$ gibt, die mit einer abgeschlossenen Untermannigfaltigkeit des $\mathbb {R} ^{2n}$ identifiziert. Das Konzept der abstrakten differenzierbaren Mannigfaltigkeit unterscheidet sich von dem der Untermannigfaltigkeit im $\mathbb {R} ^{2n}$ also nur in der Anschauung, aber nicht in seinen mathematischen Eigenschaften.

Klassifikation

Eine topologische Mannigfaltigkeit ist ein Hausdorffraum, der das zweite Abzählbarkeitsaxiom erfüllt, zusammen mit einem Atlas. Unter Umständen ist es möglich, zum Beispiel durch Reduktion der Karten im Atlas einen differenzierbaren Atlas zu erhalten und somit die topologische Mannigfaltigkeit zu einer differenzierbaren Mannigfaltigkeit zu erweitern. Jedoch kann nicht für jede topologische Mannigfaltigkeit eine differenzierbare Struktur gefunden werden. Unter Umständen ist es aber sogar möglich auf einer topologischen Mannigfaltigkeit nichtäquivalente differenzierbare Atlanten zu finden. Es gibt also auch topologische Mannigfaltigkeiten, auf denen man verschiedene differenzierbare Strukturen finden kann. Aus Sicht der Differentialgeometrie handelt es sich dann um zwei unterschiedliche Mannigfaltigkeiten, während es sich in der Topologie nur um ein Objekt handelt.

Bei der Klassifikation von differenzierbaren Mannigfaltigkeiten untersucht man die Frage, wie viele unterschiedliche differenzierbare Strukturen auf einer differenzierbaren Mannigfaltigkeit existieren. Einfacher ausgedrückt, wählt man eine differenzierbare Mannigfaltigkeit, betrachtet von dieser nur die topologische Struktur und untersucht wie viele verschiedene differenzierbare Strukturen existieren, die diese zu einer differenzierbaren Mannigfaltigkeit machen. Für differenzierbare Mannigfaltigkeiten der Dimension kleiner als vier gibt es (bis auf Diffeomorphie) nur eine differenzierbare Struktur. Für alle Mannigfaltigkeiten der Dimension größer als vier existieren endlich viele verschiedene differenzierbare Strukturen. Mannigfaltigkeiten der Dimension vier sind bezüglich der differenzierbaren Strukturen außergewöhnlich. Der $\mathbb {R} ^{4}$ als einfachstes Beispiel einer nicht kompakten vierdimensionalen differenzierbaren Mannigfaltigkeit hat überabzählbar viele verschiedene differenzierbare Strukturen, der $\mathbb {R} ^{n}$ mit $n\neq 4$ hat hingegen genau eine differenzierbare Struktur. Bei der vierdimensionalen Sphäre hingegen ist im Gegensatz zu anderen "kleineren" Dimensionen noch nicht bekannt wie viele differenzierbare Strukturen diese trägt. Die folgende Tabelle enthält die Zahl der differenzierbaren Strukturen auf den Sphären bis zur Dimension 12:

Dimension	1	2	3	4	5	6	7	8	9	10	11	12
Anzahl der differenzierbaren Strukturen	1	1	1	?	1	1	28	2	8	6	992	1

Unendlichdimensionale Mannigfaltigkeiten

Die hier vorgestellten Mannigfaltigkeiten sehen lokal aus wie der endlichdimensionale Raum $\mathbb {R} ^{n}$ , somit sind diese Mannigfaltigkeiten per Definition endlichdimensional.

Es gibt aber in der Literatur auch mehrere Ansätze, unendlichdimensionale differenzierbare Mannigfaltigkeiten zu definieren. Üblicherweise ersetzt man in der Definition den Raum $\mathbb {R} ^{n}$ durch einen lokalkonvexen topologischen Vektorraum (den sogenannten Modellraum), wie zum Beispiel einen Fréchet-Raum, einen Banachraum oder einen Hilbertraum. Man spricht dann von lokalkonvexen Mannigfaltigkeiten, Fréchet-Mannigfaltigkeiten, Banach-Mannigfaltigkeiten oder Hilbert-Mannigfaltigkeiten. Eine solche Definition ist natürlich erst sinnvoll, wenn man sich darauf geeinigt hat, wie man differenzierbare und $C^{k}$ -Abbildungen zwischen unendlichdimensionalen lokalkonvexen Räumen definiert. Während dies für Banachräume relativ unkritisch ist (Fréchet-Ableitung), gibt es für beliebige lokalkonvexe Räume unterschiedliche, nicht äquivalente Ansätze.

Beispiele für unendlichdimensionale Mannigfaltigkeiten:

die Einheitssphäre in einem Hilbertraum ist eine $C^{\infty }$ -Hilbert-Mannigfaltigkeit.
die Gruppe der unitären Operatoren auf einem Hilbertraum ist eine $C^{\infty }$ -Banach-Mannigfaltigkeit.
die Gruppe der Diffeomorphismen des Einheitskreises ist eine $C^{\infty }$ -Fréchet-Mannigfaltigkeit.

Basierend auf einem Artikel in:

Wikipedia.de