Lokalkonvexer Raum

Lokalkonvexe Räume (genauer: lokalkonvexe topologische Vektorräume) sind im mathematischen Teilgebiet der Funktionalanalysis untersuchte topologische Vektorräume mit zusätzlichen Eigenschaften. Es handelt sich dabei um topologische Vektorräume, in denen jeder Punkt über „beliebig kleine“ konvexe Umgebungen verfügt. Alternativ können lokalkonvexe Räume auch als Vektorräume definiert werden, deren Topologie durch eine Familie von Halbnormen erzeugt wird.

Die Einheitskugel im euklidischen Raum ist eine konvexe Nullumgebung.

Ein lokalkonvexer Raum kann als eine Verallgemeinerung eines normierten Vektorraumes bzw. eines normierbaren Vektorraumes betrachtet werden, denn die Normkugeln um 0 sind konvexe Umgebungen des Nullpunktes.

Geometrische Definition

Ein topologischer Vektorraum (über dem Körper $\mathbb {R}$ der reellen Zahlen oder dem Körper $\mathbb {C}$ der komplexen Zahlen) heißt lokalkonvex, wenn jede Nullumgebung (d.h. Umgebung des Nullpunktes) eine offene Teilmenge mit den folgenden drei Eigenschaften enthält:

ist konvex.
ist absorbierend.
ist ausgewogen.

Eine Teilmenge eines reellen oder komplexen Vektorraumes heißt dabei absorbierend, wenn es zu jedem Vektor in eine echt positive reelle Zahl gibt, so dass $\alpha x$ für jede reelle bzw. komplexe Zahl $\alpha$ mit $|\alpha|<r$ ein Element von ist.

Eine Teilmenge eines reellen oder komplexen Vektorraumes heißt ausgewogen, wenn zu jedem Vektor in und jeder Zahl mit |r|<1 der Vektor ebenfalls in liegt. Im Fall eines reellen Vektorraums bedeutet dies, dass die Strecke von nach in liegt; bei einem komplexen Vektorraum bedeutet es, dass die „Kreisscheibe“ $\{r x \mid r \in \C,\ |r| < 1\}$ enthält. Aufgrund dieser geometrischen Bedeutung werden solche Mengen manchmal auch kreisförmig genannt.

Eine ausgewogene und konvexe Menge heißt absolutkonvexe Menge.

Es stellt sich heraus, dass auf die zweite und dritte Bedingung verzichtet werden kann. Es gibt genau dann eine Nullumgebungsbasis aus konvexen, absorbierenden und ausgewogenen Mengen, wenn es eine Nullumgebungsbasis aus konvexen Mengen gibt. Zwei solche Umgebungsbasen müssen natürlich nicht übereinstimmen, aber die Existenz der einen impliziert die Existenz der anderen.

Definition durch Halbnormen

Lokalkonvexe Räume lassen sich auch durch Halbnormen-Systeme charakterisieren: Ein topologischer Vektorraum heißt lokalkonvex, wenn seine Topologie durch eine Familie $\mathcal{P}$ von Halbnormen definiert ist. Das heißt, ein Netz konvergiert genau dann, wenn es bezüglich aller Halbnormen aus $\mathcal{P}$ konvergiert; genauer: Es ist $x_i\rightarrow x$ genau dann, wenn $p(x_i-x)\rightarrow 0$ für alle Halbnormen $p\in \mathcal{P}$ . Die Kugeln $B_p(x,\varepsilon)=\left\{y \in V \,:\, p(x-y) < \varepsilon \right\}$ , wobei $x\in V,\, \varepsilon > 0,\, p \in \mathcal{P}$ , bilden dabei eine Subbasis der Topologie, die Mengen $B_p(0,\varepsilon)$ sind absolutkonvexe Nullumgebungen.

Ist umgekehrt eine Nullumgebungsbasis aus absolutkonvexen Mengen gegeben, so bilden die zugehörigen Minkowski-Funktionale ein definierendes Halbnormen-System.

Beispiele

Alle normierten Räume (insb. alle Banachräume) sind lokalkonvex, wobei die Familie $\mathcal{P}$ nur die (echte) Norm enthält.
Direkte Limites von Banachräumen wie $\mathcal{C}(\mathbb{R})$ mit der durch $\textstyle p_k(f)= \max_{x \in [-k,k]} |f(x)|$ gegebenen Familie von Halbnormen.
Alle topologischen Vektorräume mit der schwachen Topologie.
Banachräume mit schwacher Topologie sowie Dualräume von Banachräumen mit der schwach-*-Topologie sind lokalkonvex, wobei die Familie $\mathcal{P}$ hier durch die Funktionale aus dem Dual- respektive Prädualraum mittels $p_y\left(x\right)=|y(x)|$ (y ist das Funktional) erzeugt wird.
Projektive Limites von Banachräumen sind lokalkonvex. Die Familie $\mathcal{P}$ ist durch die Normen der Banachräume, deren Limes gebildet wird, gegeben. Als Beispiel betrachte $\mathcal{C}^\infty([0,1])$ mit der Familie der Normen
$p_k(f)= \sum_{i\leq k} \max_{x \in [0,1]} |f^{(i)}(x)|.$
Obwohl die Familie aus echten Normen besteht, ist der Raum kein Banachraum!
Der Schwartz-Raum, Folgenräume wie zum Beispiel die Köthe-Räume, Funktionenräume wie zum Beispiel Räume von Testfunktionen.
Der Raum L^p([0,1]) ist für ein topologischer (sogar metrisierbarer) Vektorraum, der nicht lokalkonvex ist.

Eigenschaften

Erfüllt die Halbnormenmenge aus obiger Definition $\{x\in V:p(x)=0\; \forall \, p \in \mathcal{P}\}=\{0\}$ , so ist der Raum ein Hausdorff-Raum. Viele Autoren betrachten nur Hausdorff’sche lokalkonvexe Räume.

Hausdorffsche, lokalkonvexe Räume haben genügend viele stetige, lineare Funktionale, um Punkte zu trennen, d.h. für alle $x,y\in V, x \not= y$ gibt es ein stetiges, lineares Funktional mit $f(x) \not= f(y)$ . Das zeigt sich in der Gültigkeit wichtiger Sätze wie

Der Satz von Hahn-Banach
Der Trennungssatz
Der Satz von Krein-Milman

Die stetigen, linearen Funktionale auf einem topologischen Vektorraum V trennen genau dann die Punkte, wenn es eine gröbere Topologie auf V gibt, die V zu einem hausdorffschen, lokalkonvexen Raum macht. Die Untersuchung lokalkonvexer Räume mittels stetiger, linearer Funktionale führt zu einer sehr weitreichenden Theorie, die für allgemeine topologische Vektorräume so nicht möglich ist. Es gibt topologische Vektorräume, die außer dem Nullfunktional kein weiteres stetiges, lineares Funktional besitzen.

Verallgemeinerungen

Spezielle Klassen lokalkonvexer Räume

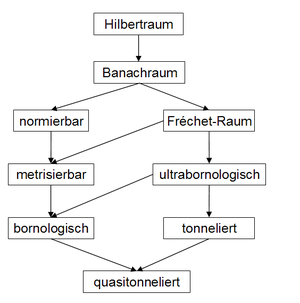
Beziehungen der Raumklassen untereinander, ein Pfeil führt von der spezielleren zur allgemeineren Raumklasse.

Viele Klassen lokalkonvexer Räume zeichnen sich durch die Gültigkeit bestimmter Sätze, die aus der Theorie der Banachräume oder normierten Räume bekannt sind, aus. So sind z.B. die tonnelierten Räume genau diejenigen lokalkonvexen Räume, in denen der Satz von Banach-Steinhaus noch gilt. Diese Sätze können in den entsprechenden Raumklassen in „Reinkultur“ untersucht werden, ihre Tragweite wird deutlich. Die bekanntesten dieser Raumklassen sind:

bornologische Räume und ultrabornologische Räume
tonnelierte Räume und quasitonnelierte Räume
metrisierbare lokalkonvexe Räume
Fréchet-Räume
normierte Vektorräume
Banachräume
Hilberträume

Räume differenzierbarer oder holomorpher Funktionen tragen natürliche lokalkonvexe Topologien, deren Eigenschaften zu weiteren Raumklassen Anlass geben. Die wichtigsten dieser Raumklassen, die zu einem tieferen Verständnis der lokalkonvexen Theorie führen, sind etwa

nukleare Räume
Montelräume
Schwartz-Räume
(DF)-Räume und gDF-Räume
quasinormierbare Räume
(LF)-Räume und LB-Räume
Räume mit Gewebe

Historische Bemerkungen

Bereits 1906 stelle M. Fréchet fest, dass der „Abschluss“ der Menge $C_b(\R)$ der beschränkten stetigen Funktionen auf $\mathbb {R}$ in der Menge aller beschränkten Funktionen auf $\mathbb {R}$ bezüglich der punktweisen Konvergenz nicht durch die Menge aller Grenzwerte von Folgen aus $C_b(\R)$ beschrieben werden kann. Der dazu erforderliche allgemeinere Umgebungsbegriff, wie er 1914 durch F. Hausdorff in der allgemeinen Topologie eingeführt wurde, fand in der Funktionalanalysis erstmals durch J. v. Neumann in seiner Beschreibung der schwachen bzw. starken Nullumgebungen in L(H) , Hilbertraum, Anwendung, wobei eine Verallgemeinerung auf Banachräume nicht versucht wurde. Der Umgebungsbegriff für allgemeinere Situationen findet sich bei S. Banach (1932) und Bourbaki (1938) in Untersuchungen über die schwach-*-Topologie, wobei man sich zunächst auf separable Räume beschränkte, damit die Einheitskugel im Dualraum metrisierbar ist. Obwohl die Untersuchung normierter Räume im Vordergrund stand, war damit klar, dass allgemeinere Raumklassen in natürlicher Weise auftreten.

S. Banach, S. Mazur und W. Orlicz betrachteten Räume, deren Topologie durch eine Folge (p_n)_n von Halbnormen gegeben ist, und definierten den Abstand

$d(x,y):=\sum _{{n=1}}^{\infty }\,{\frac {1}{n!}}\cdot {\frac {p_{n}(x-y)}{1+p_{n}(x-y)}}$ .

Für die vollständigen unter diesen Räumen, die man heute Frécheträume nennt, konnte der Satz vom abgeschlossenen Graphen bewiesen werden. Dass aber auch metrisierbare Räume nicht ausreichen, zeigte die Feststellung J. v. Neumanns aus dem Jahre 1929, dass die schwache Topologie auf unendlich-dimensionalen Hilberträumen nicht metrisierbar ist.

1934 wurden von G. Köthe und O. Toeplitz neue Typen von Räumen, sogenannte Folgenräume, eingeführt und deren Dualitätstheorie im Kontext der Folgenräume entwickelt. In diesem Zusammenhang tauchte der Begriff des starken Dualraums auf.

Die im Sinne der Metrik beschränkten Mengen verhielten sich nicht wie im Falle normierter Räume, es bedurfte einer topologischen Charakterisierung der Beschränktheit, wie sie in der unten zitierten Arbeit J. v. Neumanns aus dem Jahre 1935 gegeben wurde. Dieser Beschränktheitsbegriff findet sich im selben Jahr auch bei A. N. Kolmogorow bei dem Beweis der Aussage, dass ein hausdorffscher topologischer Vektorraum genau dann normierbar ist, wenn er eine beschränkte und konvexe Nullumgebung besitzt (Normierbarkeitskriterium von Kolmogorow). Von Neumanns Arbeit enthält auch erstmals die allgemeine Definition des lokalkonvexen Raums, die Äquivalenz der oben angegebenen geometrischen Definition und der Definition durch Halbnormen wird dort bewiesen. Dadurch konnten die Ideen von Köthe und Toeplitz in einem allgemeineren Rahmen durchgeführt werden. Meilensteine waren die Ergebnisse von G. Mackey aus dem Jahre 1946, siehe Satz von Mackey, Satz von Mackey-Arens, und die Untersuchungen von Tensorprodukten von A. Grothendieck aus dem Jahre 1953. Weitere Bedeutung erlangten die lokalkonvexen Räumen durch von L. Schwartz, A. Grothendieck, S. L. Sobolew,S. Bochner und anderen durchgeführten Untersuchungen in der Theorie der partiellen Differentialgleichungen und die damit einhergehende Begründung der Theorie der Distributionen. Der Satz vom Kern führte Grothendieck zum wichtigen Begriff des nuklearen Raums.

Siehe auch

Normierte Räume mit der schwachen Topologie, der schwach-*-Topologie oder der beschränkten schwach-*-Topologie sind lokalkonvexe Räume, die in der Theorie der normierten Räume wichtig sind.
Verschiedene Operatortopologien führen zu lokalkonvexen Räumen in der Theorie der Operatoralgebren.

Basierend auf einem Artikel in:

Wikipedia.de