Testfunktion
Als Testfunktionen bezeichnet man in der Mathematik gewisse Typen von Funktionen, die in der Distributionentheorie eine wesentliche Rolle spielen. Üblicherweise fasst man Testfunktionen eines bestimmten Typs zu einem Vektorraum zusammen. Die zugehörigen Distributionen sind dann lineare Funktionale auf diesen Vektorräumen. Ihr Name rührt daher, dass man die Distributionen (im Sinne linearer Abbildungen) auf die Testfunktionen anwendet und dadurch testet.
Es gibt verschiedene Arten von Testfunktionen. In der mathematischen Literatur werden häufig der Raum der glatten Funktionen mit kompaktem Träger oder der Schwartz-Raum als Testfunktionenraum bezeichnet.
Testfunktionen spielen eine wichtige Rolle in der Funktionalanalysis, etwa bei der Einführung des Begriffs der schwachen Ableitung, sowie in der Theorie der Differentialgleichungen. Ihre Ursprünge liegen in der Physik und den Ingenieurwissenschaften (mehr dazu im Artikel Distribution (Mathematik)).
Glatte Funktionen mit kompaktem Träger
Definition
Eines der häufigsten Beispiele für einen Testfunktionenraum ist die Menge

also der Raum aller unendlich oft differenzierbaren Funktionen, die einen kompakten Träger haben, das heißt außerhalb einer kompakten Menge gleich null sind.
Um den Raum der Testfunktionen zu erhalten, wird auf diesem Funktionenraum noch eine
Topologie
definiert. Diese Topologie erhält man aus einem Konvergenzbegriff, der auf
diesem Raum definiert wird. Eine Funktionenfolge
mit
konvergiert gegen
,
wenn es ein Kompaktum
gibt mit
für alle
und
für alle Multiindizes
gilt.
Der Raum ,
zusammen mit diesem Konvergenzbegriff, wird in der Literatur häufig mit
notiert.
Beispiele
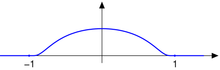
Ein Beispiel einer Testfunktion mit kompaktem Träger
ist
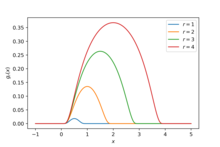
Ein weiteres Beispiel ist die Familie von -Funktionen
mit Träger
(
)
Eigenschaften
Beliebige Ableitungen von
liegen ebenfalls in
.
Das liegt an der Eigenschaft
und an der Tatsache, dass der Träger einer Funktion den Träger ihrer Ableitung
enthält.
Sei
eine offene Teilmenge von
.
- Dann ist der Testfunktionenraum ein lokalkonvexer Vektorraum, genauer ein (LF)-Raum.
- Der Testfunktionenraum
erfüllt die Heine-Borel-Eigenschaft.
- Der Raum
ist ein Unterraum des Schwartz-Raums. Er liegt sogar dicht im Schwartz-Raum und ist somit auch dicht in
für
.
Schwartz-Raum
Ein weiterer Raum, der häufig als Testfunktionenraum bezeichnet wird, ist der
Raum der schnell fallenden Funktionen, auch bekannt als der Raum der
schwartzschen Testfunktionen oder Schwartz-Raum. Sein Dualraum heißt
Raum
der temperierten Distributionen und wird mit
notiert.
Raum der glatten Funktionen
Der Raum der glatten Funktionen auf
zusammen mit ihrer lokalkonvexen
Topologie, die durch die Familie von Halbnormen
induziert wird, findet auch Anwendung als Testfunktionenraum. Dieser Raum
wird mit
notiert. Sein Dualraum
ist der Raum der Distributionen
mit kompaktem Träger.
Sobolev-Räume
Auch der Sobolev-Raum
für eine beliebige reelle Zahl
kann als Testfunktionenraum aufgefasst werden. Dieser Unterraum von
ist ebenfalls ein Hilbertraum.
Bezüglich der dualen
Paarung
ist allerdings
der entsprechende Distributionenraum.
Der Satz von Riesz-Markov
Mit Hilfe des Darstellungssatzes
von Riesz-Markow lässt sich der Dualraum des Raums der stetigen Funktionen
auf einem kompakten Definitionsbereich
schreiben als
wobei
der Raum der regulären Borelmaße ist. Die Isomorphie ist dadurch gegeben, dass
ein Funktional
stets in der Form
geschrieben werden kann. Die Integralschreibweise legt nahe, dass es auch für diese beiden Räume möglich ist, Distributionentheorie zu betreiben.
Allgemeinere Testfunktionenräume
Prinzipiell lässt sich das Konzept von Testfunktionen und Distributionen auf
andere Beispiele übertragen, in denen man einen Funktionenraum und seinen Dualraum zur
Verfügung hat. Der Grundgedanke besteht darin, dass man einen Vektorraum
von Funktionen betrachtet. Da man häufig auf Begriffe wie Stetigkeit und Konvergenz
zurückgreifen möchte, sollte der Vektorraum ein topologischer
Vektorraum oder besser noch ein lokalkonvexer
Raum sein. Die Distributionen, die zu dem Raum
gehören sind dann Elemente des topologischen
Dualraums
.
Mit Hilfe der dualen
Paarung kann man das Anwenden einer Distribution
auf eine Testfunktion
in der Form
schreiben. Die Notation erinnert stark an ein Skalarprodukt,
und in der Tat denkt man dabei häufig an das -Skalarprodukt,
so dass man (formal) auch
schreibt (beachte, dass
keine Funktion ist und das Integral daher nicht immer wohldefiniert ist). Damit
diese Interpretation einen Sinn ergibt, verlangt man in aller Regel, dass der
Raum
ein stetig eingebetteter Teilraum eines Vektorraums integrierbarer Funktionen
ist, z.B.
oder
.
Literatur
- Hui-Hsiung Kuo: White Noise Distribution Theory, CRC Press, 1996, ISBN 0-8493-8077-4.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 29.06. 2020