Produktregel
Die Produktregel oder Leibnizregel (nach G. W. Leibniz) ist eine grundlegende Regel der Differentialrechnung. Sie führt die Berechnung der Ableitung eines Produktes von Funktionen auf die Berechnung der Ableitungen der einzelnen Funktionen zurück.
Eine Anwendung der Produktregel in der Integralrechnung ist die Methode der partiellen Integration. Für den Fall, dass eine der beiden Funktionen konstant ist, geht die Produktregel in die einfachere Faktorregel über.
Aussage der Produktregel
Sind die Funktionen
und
von einem Intervall
in die Menge der reellen
oder der komplexen
Zahlen an einer Stelle
differenzierbar, so ist auch die durch
für alle
definierte Funktion
an der Stelle
differenzierbar, und es gilt
oder kurz:
Anwendungsbeispiele
Im Folgenden sei stets
- Ist
und
so erhält man aus der Kenntnis von
und
mit der Produktregel die Aussage
- Ist
und
so ist
also ist
-
- und durch Umformen erhält man die Aussage
Verwendet man die Kurznotation
so erhält man beispielsweise für die Ableitung folgender Funktion
Ausmultipliziert ergibt sich
Erklärung und Beweis
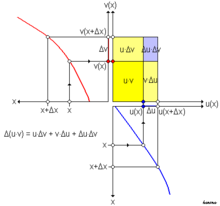
Das Produkt
zweier reeller (an einer Stelle
differenzierbarer) Funktionen
und
hat an der Stelle
den Wert
der als Flächeninhalt eines Rechtecks mit den Seiten
und
gedeutet werden kann. Ändert sich nun
um
so ändert sich
um
und
um
Die Änderung
des Flächeninhalts
setzt sich dann (siehe Abbildung) zusammen aus
Dividiert man durch
so ergibt sich mit
der Differenzenquotient
der Produkt- oder Flächeninhaltsfunktion
an der Stelle
Für
gegen
strebt auch
(und damit der ganze letzte Summand) gegen
sodass man an der Stelle
erhält, wie behauptet. Dies ist auch im Wesentlichen die Argumentation, wie
sie sich in einem ersten Beweis der Produktregel 1677 in einem Manuskript von
Leibniz findet. Die Produktregel, die er dort gemeinsam mit der Quotientenregel
beweist, war damit eine der ersten Regeln zur Anwendung der Infinitesimalrechnung,
die er herleitete. Er benutzte allerdings keinen Grenzwert, sondern
noch Differentiale
und schloss, dass
wegfällt, weil es im Vergleich zu den anderen Summanden infinitesimal klein sei.
Euler benutzte noch
dasselbe Argument, erst bei Cauchy findet
sich ein Beweis mit Grenzwerten:
Gegeben sei die Funktion
durch
Die Ableitung
von
an einer Stelle
ist dann durch den Grenzwert des Differenzenquotienten
gegeben. Addition und Subtraktion des Terms
liefert
Das Ausführen der beiden Grenzübergänge liefert die Produktregel
Verallgemeinerungen
Produkte von Vektoren und Matrix-Vektor-Produkte
Beim Beweis der Produktregel werden aus den Werten von
Linearkombinationen
(Summen, Differenzen, Produkte mit Zahlen) gebildet, ebenso aus den Werten von
Die Rollen von
und
sind dabei klar getrennt:
ist der linke Faktor,
der rechte. Der Beweis überträgt sich deswegen auf alle Produktbildungen, die
sowohl im linken als auch im rechten Faktor linear sind. Insbesondere gilt die
Produktregel auch für
- Skalarprodukte von zwei Vektoren
- Vektorprodukte (Kreuzprodukte) von zwei Vektoren
- Matrix-Vektor-Produkte.
Vektoren bzw. Matrizen sind dabei als Funktionen einer unabhängigen Variablen zu verstehen.
Mehr als zwei Faktoren
Die Produktregel kann sukzessive auch auf mehrere Faktoren angewandt werden. So wäre
und
usw.
Allgemein ist für eine Funktion
die sich als Produkt von
Funktionen
schreiben lässt, die Ableitung
Haben die Funktionen keine Nullstellen, so kann man diese Regel auch in der übersichtlichen Form
(oder kurz:
)
schreiben; derartige Brüche bezeichnet man als logarithmische Ableitungen.
Höhere Ableitungen
Auch die Regel für Ableitungen -ter
Ordnung für ein Produkt aus zwei Funktionen war schon Leibniz bekannt und wird
entsprechend manchmal ebenfalls als Leibnizsche Regel bezeichnet. Sie
ergibt sich aus der Produktregel mittels vollständiger
Induktion zu
Die hier auftretenden Ausdrücke der Form
sind Binomialkoeffizienten.
Die obige Formel enthält die eigentliche Produktregel als Spezialfall. Sie hat
auffallende Ähnlichkeit zum binomischen
Lehrsatz
Diese Ähnlichkeit ist kein Zufall, der übliche Induktionsbeweis läuft in beiden Fällen vollkommen analog; man kann die Leibnizregel aber auch mit Hilfe des binomischen Satzes beweisen.
Für höhere Ableitungen von mehr als zwei Faktoren lässt sich ganz entsprechend das Multinomialtheorem übertragen. Es gilt:
Höherdimensionaler Definitionsbereich
Verallgemeinert man auf Funktionen mit höherdimensionalem Definitionsbereich,
so lässt sich die Produktregel wie folgt formulieren: Es seien
eine offene Teilmenge,
differenzierbare Funktionen und
ein Richtungsvektor. Dann gilt die Produktregel für die Richtungsableitung:
Entsprechend gilt für die Gradienten
In der Sprache der differenzierbaren Mannigfaltigkeiten lauten diese beiden Aussagen:
- Sind
ein Tangentialvektor und
lokal differenzierbare Funktionen, dann gilt
- Sind
lokal differenzierbare Funktionen, so gilt die folgende Beziehung zwischen den äußeren Ableitungen:
Höhere partielle Ableitungen
Sei
Dann gilt:
Holomorphe Funktionen
Die Produktregel gilt auch für komplex
differenzierbare Funktionen: Es sei
und
holomorph.
Dann ist
holomorph, und es gilt
Allgemeine differenzierbare Abbildungen
Es seien
ein offenes Intervall,
eine Banachalgebra (z.B.
die Algebra der reellen oder komplexen
-Matrizen)
und
differenzierbare Funktionen. Dann gilt:
Dabei bezeichnet »·« die Multiplikation in der Banachalgebra.
Sind allgemeiner
und
Banachräume,
und
differenzierbare Funktionen, so gilt ebenfalls eine Produktregel, wobei die
Funktion des Produktes von einer Bilinearform
übernommen wird. Von dieser wird verlangt, dass sie stetig ist, also beschränkt:
für alle
mit einer festen Konstante .
Dann gilt die Produktregel
Entsprechende Aussagen gelten für höherdimensionale Definitionsbereiche.
Leibniz-Regel für dividierte Differenzen
Die Leibnizregel lässt sich auf dividierte Differenzen übertragen:
Der Spezialfall
schließt die originale Leibnizregel mit ein.
Abstraktion: Derivationen
Allgemein nennt man Abbildungen
welche die Produktregel
erfüllen, Derivationen. Die Reihenfolge der Faktoren ist hier für den Fall
einer Derivation
mit einer Algebra
und einem
-Linksmodul
gewählt.
Im Zusammenhang mit -
oder
-graduierten
Algebren („Superalgebren“)
muss der Begriff der Derivation jedoch durch den der Antiderivation ersetzt
werden. Die entsprechende Gleichung lautet dann
für homogene Elemente
Dabei bezeichnet
den Grad von
Das prominenteste Beispiel einer Antiderivation ist die äußere
Ableitung für Differentialformen
Literatur
Die Produktregel für Funktionen wird in jedem Buch erläutert, das Differentialrechnung in allgemeiner Form behandelt.
- Otto Forster: Analysis 1. Differential- und Integralrechnung einer Veränderlichen. 7. Auflage. Vieweg, Braunschweig 2004, ISBN 3-528-67224-2.
- Otto Forster: Analysis 2. Differentialrechnung im Rn. Gewöhnliche Differentialgleichungen. 6. Auflage. Vieweg, Braunschweig 2005, ISBN 3-528-47231-6.
- Konrad Königsberger: Analysis. 2 Bde. Springer, Berlin 2004, ISBN 3-540-41282-4.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 03.10. 2021