Matrix-Vektor-Produkt

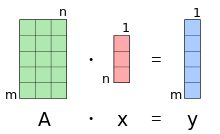
Bei einer Matrix-Vektor-Multiplikation muss die Spaltenzahl der Matrix gleich der Zahl der Komponenten des Vektors sein. Die Komponentenzahl des Ergebnisvektors entspricht dann der Zeilenzahl der Matrix.

Das Matrix-Vektor-Produkt ist in der linearen Algebra das Produkt einer Matrix mit einem Vektor. Damit eine solche Matrix-Vektor-Multiplikation durchgeführt werden kann, muss die Spaltenzahl der Matrix mit der Zahl der Komponenten des Vektors übereinstimmen. Das Ergebnis ist dann wieder ein Vektor, dessen Elemente durch komponentenweise Multiplikation und Summation der Einträge der entsprechenden Zeile der Matrix mit den Elementen des Ausgangsvektors ermittelt werden. Das Matrix-Vektor-Produkt kann als Spezialfall einer Matrizenmultiplikation angesehen werden, bei der die zweite Matrix aus nur einer Spalte besteht.

Das Matrix-Vektor-Produkt wird beispielsweise in der Matrixschreibweise linearer Gleichungssysteme sowie bei iterativen Verfahren zu ihrer numerischen Lösung eingesetzt. Weiter kann jede lineare Abbildung zwischen endlichdimensionalen Vektorräumen nach Wahl entsprechender Basen als Matrix-Vektor-Produkt dargestellt werden.

Definition

Zur Berechnung des Matrix-Vektor-Produkts wird jede Zeile der Matrix mit den Einträgen des Vektors kombiniert.

Ist ein Körper (meist die reellen oder komplexen Zahlen), dann ist die Matrix-Vektor-Multiplikation eine Abbildung

$\cdot ~ \colon K^{m \times n} \times K^n \to K^m, \quad (A,x) \mapsto y = A \cdot x$ ,

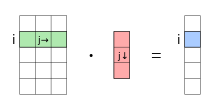
die einer Matrix $A=(a_{ij})$ und einem Vektor x = (x_j) einen weiteren Vektor y = (y_i) zuordnet. Die Matrix-Vektor-Multiplikation ist dabei nur für den Fall definiert, dass die Spaltenzahl der Matrix mit der Zahl der Komponenten des Vektors übereinstimmt. Die Komponentenzahl des Ergebnisvektors entspricht dann der Zeilenzahl der Matrix . Jedes Element $y_{i}$ des Ergebnisvektors berechnet sich dabei über

$y_i = \sum_{j=1}^n a_{ij} \cdot x_j$ ,

also durch komponentenweise Multiplikation der Einträge der -ten Zeile von mit den Elementen von und durch Summation über diese Produkte. Häufig wird bei der Notation eines Matrix-Vektor-Produkts der Malpunkt weggelassen und man schreibt kurz statt $A \cdot x$ .

Beispiel

Gegeben sei die reelle Matrix und der reelle (Spalten-)Vektor

$A = \begin{pmatrix} 3 & 2 & 1 \\ 1 & 0 & 2 \end{pmatrix} \in \R^{2 \times 3}$ und $x = \begin{pmatrix} 1 \\ 0 \\ 4 \end{pmatrix} \in \R^3$ .

Da die Matrix ebenso viele Spalten besitzt, wie der Vektor lang ist, ist das Matrix-Vektor-Produkt $A \cdot x$ definiert, die betreffende Matrix-Vektor-Multiplikation also überhaupt durchführbar. Nachdem zwei Zeilen hat, wird der Ergebnisvektor ebenfalls zwei Elemente aufweisen. Um das erste Element des Ergebnisvektors zu berechnen, betrachtet man die erste Zeile von , multipliziert die jeweils entsprechenden Einträge dieser Zeile mit denen des Ausgangsvektors und summiert die Ergebnisse auf (die Sternchen stehen für noch nicht berechnete Elemente):

$\begin{pmatrix} \color{OliveGreen} 3 & \color{OliveGreen} 2 & \color{OliveGreen} 1 \\ 1 & 0 & 2 \end{pmatrix} \cdot \begin{pmatrix} \color{BrickRed} 1 \\ \color{BrickRed} 0 \\ \color{BrickRed} 4 \end{pmatrix} = \begin{pmatrix} {\color{OliveGreen} 3} \cdot {\color{BrickRed} 1} + {\color{OliveGreen} 2} \cdot {\color{BrickRed} 0} + {\color{OliveGreen} 1} \cdot {\color{BrickRed} 4} \\ \ast \end{pmatrix} = \begin{pmatrix} {\color{Blue} 7} \\ \ast \end{pmatrix}$

Für das zweite Element des Ergebnisvektors betrachtet man entsprechend die zweite Zeile von und berechnet analog:

$\begin{pmatrix} 3 & 2 & 1 \\ \color{OliveGreen} 1 & \color{OliveGreen} 0 & \color{OliveGreen} 2 \end{pmatrix} \cdot \begin{pmatrix} \color{BrickRed} 1 \\ \color{BrickRed} 0 \\ \color{BrickRed} 4 \end{pmatrix} = \begin{pmatrix} 7 \\ {\color{OliveGreen} 1} \cdot {\color{BrickRed} 1} + {\color{OliveGreen} 0} \cdot {\color{BrickRed} 0} + {\color{OliveGreen} 2} \cdot {\color{BrickRed} 4} \end{pmatrix} = \begin{pmatrix} 7 \\ {\color{Blue} 9} \end{pmatrix}$

Als Ergebnis erhält man so am Ende das Matrix-Vektor-Produkt $y = A \cdot x$ .

Eigenschaften

Das Matrix-Vektor-Produkt ist assoziativ in dem Sinne, dass für Matrizen $A \in K^{l \times m}$ , $B \in K^{m \times n}$ und Vektoren $x \in K^n$

$A \cdot (B \cdot x) = ( A \cdot B ) \cdot x$

gilt. Das Matrix-Vektor-Produkt ist auch verträglich mit der Multiplikation von Skalaren $a \in K$ , das heißt

$a \, (A \cdot x) = ( a \, A ) \cdot x = A \cdot ( a \, x )$ .

Betrachtet man die komponentenweise Matrizenaddition A + B zweier Matrizen $A,B \in K^{m \times n}$ sowie die Vektoraddition zweier Vektoren $x,y \in K^n$ , dann sind auch die Distributivgesetze erfüllt, das heißt

$(A + B) \cdot x = A \cdot x + B \cdot x$

und

$A \cdot (x + y) = A \cdot x + A \cdot y$ .

Algorithmus

In Pseudocode kann das Matrix-Vektor-Produkt wie folgt implementiert werden:

function matrix-vector-product(A,x,m,n)
  y = zeroes(m)                      // Ergebnisvektor y mit Nullen initialisieren
  for i = 1 to m                     // Schleife über die Zeilen von A
    for j = 1 to n                   // Schleife über die Elemente von x
      y(i) = y(i) + A(i,j) * x(j)    // Bildung der Produktsumme
    end
  end
  return y

Die Reihenfolge der beiden For-Schleifen kann dabei auch vertauscht werden. Da die beiden Schleifen unabhängig voneinander sind, ist die Anzahl der benötigten arithmetischen Operationen von der Ordnung

$O(m \cdot n)$ .

Die Laufzeit des Algorithmus ist für quadratische Matrizen (m=n) demnach von der Ordnung O(n^2) . Spezielle Matrizen, wie Bandmatrizen, dünnbesetzte Matrizen oder Toeplitz-Matrizen, können durch Ausnutzen der Struktur auch effizienter mit einem Vektor multipliziert werden.

Geometrische Interpretation

Im bis zu 3-dimensionalen Fall einer Multiplikation von einer Matrix mit einem Vektor kann man schon anhand der Zahlen in der Matrix erkennen, wie die Matrix als lineare Abbildung "aussieht". Sei zum Beispiel eine 2-dimensionale Ebene mit den Basisvektoren

${\vec {x}}={\begin{pmatrix}1\\0\end{pmatrix}},{\vec {y}}={\begin{pmatrix}0\\1\end{pmatrix}}$ gegeben. Einen Vektor in dem 2-dimensionalen Vektorraum wird mit Hilfe der Basisvektoren dargestellt. Meistens werden implizit diese beiden Basisvektoren benutzt. Möchte man zum Beispiel den Vektor ${\vec {v}}={\begin{pmatrix}4\\7\end{pmatrix}}$ als Linearkombination mit diesen Basisvektoren darstellen, so setzt sich der Vektor ${\vec {v}}$ durch ${\vec {v}}=4\cdot {\vec {x}}+7\cdot {\vec {y}}=4\cdot {\begin{pmatrix}1\\0\end{pmatrix}}+7\cdot {\begin{pmatrix}0\\1\end{pmatrix}}$ zusammen. Setzt man die Basisvektoren ${\vec {x}}$ und ${\vec {y}}$ als Matrix zusammen, erhält man ${\begin{pmatrix}1&0\\0&1\end{pmatrix}}$ . Das ist die Einheitsmatrix $E_{2}$ . Möchte man zum Beispiel mit einer Matrix eine lineare Abbildung beschreiben, die eine 90° Drehung gegen den Uhrzeigersinn beschreibt, so kann man sich vorstellen, der ${\vec {x}}$ Basisvektor sich dreht und dann zu ${\begin{pmatrix}0\\1\end{pmatrix}}$ wird. Dreht man den ${\vec {y}}$ Basisvektor um 90° gegen den Uhrzeigersinn, ergibt sich intuitiv ${\begin{pmatrix}-1\\0\end{pmatrix}}$ . Die Matrix, die nun die 90° Rotation gegen den Uhrzeigersinn beschreibt, ist damit ${\begin{pmatrix}0&-1\\1&0\end{pmatrix}}$ . Aus dieser Betrachtungsweise kann man die Zahlen in einer Matrix geometrisch interpretieren.

Verwendung

Das Matrix-Vektor-Produkt wird in der linearen Algebra häufig verwendet. So ist die Matrixschreibweise eines linearen Gleichungssystems

$A\cdot x=b$

nichts anderes als eine Vektorgleichung, auf deren linken Seite ein Matrix-Vektor-Produkt steht. Viele iterative Verfahren zur numerischen Lösung linearer Gleichungssysteme, wie das Verfahren der konjugierten Gradienten oder allgemeine Krylow-Unterraum-Verfahren, basieren auf wiederholten Matrix-Vektor-Multiplikationen. Auch die Potenzmethode zur Ermittlung des betragsgrößten Eigenwerts einer Matrix basiert auf der wiederholten Berechnung von Matrix-Vektor-Produkten.

Sind allgemein und zwei endlichdimensionale Vektorräume über dem gleichen Körper, dann kann jede lineare Abbildung $f\colon V\to W$ nach Wahl je einer Basis in beiden Vektorräumen über ihre Abbildungsmatrix M_f dargestellt werden. Das Bild eines Vektors unter der Abbildung in den jeweiligen Basen kann dann über das Matrix-Vektor-Produkt

$y = M_f \cdot x$

ermittelt werden. In der Geometrie lässt sich beispielsweise auf diese Weise jede Drehung um den Ursprung und jede Spiegelung an einer Ursprungsebene durch ein solches Matrix-Vektor-Produkt ausführen. Auch diskrete Faltungen, beispielsweise die diskrete Fourier-Transformation, können als Matrix-Vektor-Produkt realisiert werden.

Literatur

Charles Leiserson, Ronald L. Rivest, Clifford Stein: Algorithmen – eine Einführung. Oldenbourg, 2010, ISBN 3-486-59002-2.

Basierend auf einem Artikel in:

Wikipedia.de