Potenzmethode
Die Potenzmethode, Vektoriteration oder
von-Mises-Iteration (nach Richard von Mises)
ist ein numerisches
Verfahren zur Berechnung des betragsgrößten Eigenwertes und des
dazugehörigen Eigenvektors einer Matrix.
Der Name kommt daher, dass Matrixpotenzen
gebildet werden, wesentlicher Aufwand sind also Matrix-Vektor-Produkte.
Deswegen ist das Verfahren insbesondere für dünnbesetzte
Matrizen geeignet. Eine direkte Verallgemeinerung zur Berechnung mehrerer
betragsgrößter Eigenwerte dünnbesetzter
Matrizen ist die Unterraumiteration.
Die Potenzmethode lässt sich als nicht-optimales Krylow-Unterraum-Verfahren interpretieren, welches nur den jeweils letzten berechneten Vektor zur Eigenwertnäherung verwendet. Die Potenzmethode ist hinsichtlich der Konvergenzgeschwindigkeit den anderen Krylow-Raum-Verfahren, wie etwa dem Verfahren von Lanczos oder dem Verfahren von Arnoldi unterlegen. Dafür schneidet die Potenzmethode hinsichtlich der Stabilitätsanalyse besser ab.
Der Algorithmus
Motivation
Aus der Stochastik abgeleitet gibt
es folgenden naiven Ansatz zur Eigenwertberechnung: Betrachtet man einen stochastischen
Startvektor
und eine spaltenstochastische
Matrix
,
dann ist die Wahrscheinlichkeitsverteilung einer Markow-Kette
zum Zeitpunkt
genau
.
Falls nun die
gegen einen Vektor
konvergieren, so ist
und wir haben eine vom Anfangszustand unabhängige stationäre
Verteilung und damit auch einen Eigenvektor zum Eigenwert 1 gefunden. Formal
ist also
,
es wurden Matrixpotenzen gebildet. Dieses Verfahren lässt sich nun für beliebige
Matrizen verallgemeinern.
Allgemeiner Algorithmus
Gegeben sei eine quadratische Matrix
und ein Startvektor
mit
.
In jedem Iterationsschritt wird die Matrix
auf die aktuelle Näherung
angewandt und dann normiert.
oder in geschlossener Form
Die Vektoren
konvergieren gegen einen Eigenvektor zum betragsgrößten Eigenwert, sofern dieser
Eigenwert halbeinfach
ist und alle anderen Eigenwerte einen echt kleineren Betrag haben. Es existiert
also ein Index
,
so dass für die Eigenwerte gilt
und
.
Hierbei ist
die geometrische (und algebraische) Vielfachheit des Eigenwerts
.
Der zum Vektor
gehörende approximierte Eigenwert kann auf zwei Arten berechnet werden:
- Bildet man die Skalare
(den sogenannten Rayleigh-Quotient), so konvergiert
gegen
. Dies folgt direkt aus der Konvergenz von
gegen einen Eigenvektor.
- Ist man nicht am Vorzeichen des Eigenwertes interessiert, so bietet sich
ein einfacher Ansatz an: Da
gegen einen Eigenvektor konvergiert und in jedem Schritt auf 1 normiert wird, konvergiert
gegen
(unabhängig von der verwendeten Norm).
Beweis der Konvergenz
Wir geben hier einen Beweis unter der Annahme, dass die Matrix
diagonalisierbar ist. Der Beweis für den nichtdiagonalisierbaren Fall läuft
analog.
O.B.d.A.
seien die Eigenwerte wie oben angeordnet. Sei
die Basiswechselmatrix
zur Matrix
.
Dann ist
wobei
nach Voraussetzung eine Diagonalmatrix ist, welche die Eigenwerte enthält. Sei
nun
eine Basis aus Eigenvektoren (die Spaltenvektoren von
)
und
ein Startvektor mit
Dann ist
Da nach der Voraussetzung gilt, dass .
Wegen
wird in jedem Schritt die Normierung des Vektors auf 1 durchgeführt. Die oben angegebene Bedingung an den Startvektor besagt, dass er einen Nichtnullanteil in Richtung des Eigenvektors haben muss. Dies ist aber meist nicht einschränkend, da sich diese Bedingung durch Rundungsfehler in der Praxis oftmals von alleine ergibt.
Konvergenzgeschwindigkeit
Unter der häufigen starken Voraussetzung, dass der Eigenwert einfach,
betragsmäßig einfach und gut separiert ist, konvergieren sowohl die
Eigenwertnäherungen als auch die Eigenvektornäherungen linear mit der
Konvergenzgeschwindigkeit ,
wobei die Eigenwerte dem Betrage nach abfallend sortiert angenommen werden,
.
Diese Voraussetzung ist zum Beispiel nach dem Satz von
Perron-Frobenius bei Matrizen mit positiven Einträgen erfüllt. Des Weiteren
haben noch Jordanblöcke einen Einfluss auf die Konvergenzgeschwindigkeit.
Betrachte dazu als Beispiel die Matrizen
und
Beide haben den Eigenvektor
zum betragsgrößten Eigenwert
und die Separation der Eigenwerte ist
.
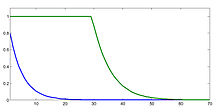
Unter Verwendung der Maximumsnorm
und des Startvektors
konvergiert die Matrix
mit linearer Konvergenzgeschwindigkeit, während die Matrix
erst nach ca. 60 Iterationsschritten ein brauchbares Ergebnis liefert
(vergleiche Bild).
Verwendung
Da zur Berechnung des Gleichgewichtszustandes großer Markow-Ketten nur der Eigenvektor zum betragsgrößten Eigenwert bestimmt werden muss, kann hierfür die Potenzmethode verwendet werden, wie bereits im Abschnitt „Motivation“ beschrieben wurde. Insbesondere kann hier auf die Normierung in jedem Rechenschritt verzichtet werden, da die betrachtete Matrix stochastisch ist und damit die Betragsnorm des stochastischen Vektors erhält. Ein Beispiel dafür ist die Berechnung der PageRanks eines großen gerichteten Graphen als betragsgrößten Eigenvektor der Google-Matrix. Insbesondere sind bei der Google-Matrix die Eigenwerte gut separiert, sodass eine schlechte Konvergenzgeschwindigkeit ausgeschlossen werden kann.
Varianten
Hat man einen Eigenwert
ausgerechnet, kann man das Verfahren auf die Matrix
anwenden, um ein weiteres Eigenwert-Eigenvektor-Paar zu bestimmen. Darüber
hinaus gibt es die inverse
Iteration, bei der das Verfahren auf
angewandt wird, indem in jedem Schritt lineare Gleichungssysteme gelöst werden.
Vergleiche mit anderen Krylowraum-Verfahren
Die Potenzmethode ist den anderen Krylowraum-Verfahren sehr ähnlich. Es finden sich die typischen Bestandteile der komplexeren Verfahren wieder, so etwa die Normierung der konstruierten Basisvektoren, die Erweiterung des Krylowraumes und die Berechnung von (Elementen von) Projektionen im letzten Schritt.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 31.03. 2023