Basiswechsel (Vektorraum)

Der Basiswechsel oder die Basistransformation ist ein Begriff aus dem mathematischen Teilgebiet der linearen Algebra. Man bezeichnet damit den Übergang zwischen zwei verschiedenen Basen eines endlichdimensionalen Vektorraums über einem Körper . Dadurch ändern sich im Allgemeinen die Koordinaten der Vektoren und die Abbildungsmatrizen von linearen Abbildungen. Ein Basiswechsel ist somit ein Spezialfall einer Koordinatentransformation.

Der Basiswechsel kann durch eine Matrix beschrieben werden, die Basiswechselmatrix, Transformationsmatrix oder Übergangsmatrix genannt wird. Mit dieser lassen sich auch die Koordinaten bezüglich der neuen Basis ausrechnen. Stellt man die Basisvektoren der alten Basis als Linearkombinationen der Vektoren der neuen Basis dar, so bilden die Koeffizienten dieser Linearkombinationen die Einträge der Basiswechselmatrix.

Basiswechselmatrix

Kommutatives Diagramm

Es sei ein -dimensionaler Vektorraum über dem Körper (zum Beispiel dem Körper $\mathbb {R}$ der reellen Zahlen). In seien zwei geordnete Basen gegeben, $B = ( b_1, \ldots, b_n )$ und $B' = ( b_1', \ldots, b_n' )$ .

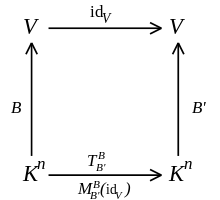
Die Basiswechselmatrix $T_{B'}^{B}$ für den Basiswechsel von nach ist eine $n\times n$ -Matrix. Es handelt sich um die Abbildungsmatrix der Identitätsabbildung auf bezüglich der Basen im Urbild und im Bild:

$T _{B'}^B = M_{B'}^{B}(\operatorname{id_V})$

Man erhält sie, indem man die Vektoren der alten Basis als Linearkombinationen der Vektoren der neuen Basis B{}' darstellt:

$b_j = a_{1j} b_1{}' + a_{2j} b_2{}' + \dots + a_{nj} b_n{}' = \sum_{i = 1}^n a_{ij} b_i{}', \qquad j = 1, \dots, n$

Die Koeffizienten $a_{1j}, \dots, a_{nj}$ bilden die -te Spalte der Basiswechselmatrix

$T _{B'}^B = \begin{pmatrix} a_{11} & \cdots & a_{1j} & \cdots & a_{1n} \\ \vdots & & \vdots & & \vdots \\ a_{n1} & \cdots & a_{nj} & \cdots & a_{nn} \end{pmatrix}$

Diese Matrix ist quadratisch und invertierbar und somit ein Element der allgemeinen linearen Gruppe $\mathrm {GL} \left(n,K\right)$ . Ihre Inverse $( T_{B'}^{B} )^{-1} = T_B^{B'}$ beschreibt den Basiswechsel von zurück nach .

Spezialfälle

Ein wichtiger Spezialfall ist der Fall V = K^n , der Vektorraum stimmt also mit dem Koordinatenraum überein. In diesem Fall sind die Basisvektoren Spaltenvektoren

$b_1 = \begin{pmatrix} b_{11} \\ \vdots \\ b_{n1} \end{pmatrix}, \dots, b_j = \begin{pmatrix} b_{1j} \\ \vdots \\ b_{nj} \end{pmatrix}, \dots, b_n = \begin{pmatrix} b_{1n} \\ \vdots \\ b_{nn} \end{pmatrix}, \quad b_1' = \begin{pmatrix} b_{11}' \\ \vdots \\ b_{n1}' \end{pmatrix}, \dots, b_j' = \begin{pmatrix} b_{1j}' \\ \vdots \\ b_{nj}' \end{pmatrix}, \dots, b_n' = \begin{pmatrix} b_{1n}' \\ \vdots \\ b_{nn}' \end{pmatrix}, \quad$

die sich zu Matrizen

$B = \begin{pmatrix} b_{11} & \dots & b_{1j} & \dots & b_{1n} \\ \vdots & & \vdots & & \vdots \\ b_{i1} & \dots & b_{ij} & \dots & b_{in} \\ \vdots & & \vdots & & \vdots \\ b_{n1} & \dots & b_{nj} & \dots & b_{nn} \end{pmatrix} \quad \text{ und } \quad B' = \begin{pmatrix} b_{11}' & \dots & b_{1j}' & \dots & b_{1n}' \\ \vdots & & \vdots & & \vdots \\ b_{i1}' & \dots & b_{ij}' & \dots & b_{in}' \\ \vdots & & \vdots & & \vdots \\ b_{n1}' & \dots & b_{nj}' & \dots & b_{nn}' \end{pmatrix}$

zusammenfassen lassen, die hier der Einfachheit halber mit den gleichen Buchstaben wie die zugehörigen Basen bezeichnet werden. Die Bedingung

$b_j = a_{1j} b_1{}' + a_{2j} b_2{}' + \dots + a_{nj} b_n{}' = \sum_{i = 1}^n a_{ij} b_i{}', \qquad j = 1, \dots, n$

übersetzt sich dann zu

$b_{kj}= \sum_{i = 1}^n a_{ij} b_{ki}{}' = \sum_{i = 1}^n b_{ki}{}' a_{ij} , \qquad k, j = 1, \dots, n,$

das heißt,

$B = B' \cdot T^B_{B'}.$

Die Transformationsmatrix $T^B_{B'}$ lässt sich somit durch

$T^B_{B'} = (B')^{-1} \cdot B$

berechnen, wobei $(B')^{-1}$ die inverse Matrix der Matrix ist.

Insbesondere gilt: Ist die Standardbasis, so gilt $T^B_{B'} = (B')^{-1}$ . Ist die Standardbasis, so gilt $T^B_{B'} = B$ .

Wie im Vorangehenden wird hier die Basis mit der Matrix identifiziert, die man erhält, indem man die Basisvektoren als Spaltenvektoren schreibt und diese zu einer Matrix zusammenfasst.

Koordinatentransformation

Ein Vektor $v\in V$ habe bezüglich der Basis $B = (b_1, \dots, b_n)$ die Koordinaten $x_{1},\dots ,x_{n}$ , d.h.

$v = x_1 b_1 + x_2 b_2+ \dots + x_n b_n = \sum_i x_i \, b_i,$

und bezüglich der neuen Basis $B' = (b_1', \dots, b_n')$ die Koordinaten $x_1', \dots, x_n'$ , also

$v = x_1{}' b_1{}' + x_2{}' b_2{}'+ \dots + x_n{}' b_n{}' =\sum_j x_j{}' \,b_j{}'.$

Stellt man wie oben die Vektoren $b_{j}$ der alten Basis als Linearkombination der neuen Basis dar, so erhält man

$v = \sum_j x_j b_j = \sum_j x_j \sum_i a_{ij} \,b_i{}' = \sum_i \left(\sum_j a_{ij} \, x_j\right) b_i{}'$

Dabei sind die $a_{ij}$ die oben definierten Einträge der Basiswechselmatrix $T_{B'}^{B}$ . Durch Koeffizientenvergleich erhält man

$x_i{}' = \sum_{j=1}^n a_{ij} \, x_j,$

bzw. in Matrizenschreibweise:

${\begin{pmatrix}x_{1}{}'\\\vdots \\x_{n}{}'\end{pmatrix}}={\begin{pmatrix}a_{11}&\dots &a_{1n}\\\vdots &\ddots &\vdots \\a_{n1}&\dots &a_{nn}\end{pmatrix}}{\begin{pmatrix}x_{1}\\\vdots \\x_{n}\end{pmatrix}}$

oder kurz:

$x{}' = T_{B'}^B \,x$

Basiswechsel bei Abbildungsmatrizen

Die Darstellungsmatrix einer linearen Abbildung hängt von der Wahl der Basen im Urbild- und im Zielraum ab. Wählt man andere Basen, so erhält man auch andere Abbildungsmatrizen.

Kommutatives Diagramm der beteiligten Abbildungen. Mit wird hier die lineare Abbildung von $K^{n}$ nach bezeichnet, die $(x_1, \dots, x_n)$ auf $x_1 a_1 + \dots + x_n a_n$ abbildet, etc.

Seien ein -dimensionaler und ein -dimensionaler Vektorraum über und $f\colon V\to W$ eine lineare Abbildung. In seien die geordneten Basen $A = (a_1, \dots, a_n)$ und $A' = (a_1{}', \dots, a_n{}')$ gegeben, in die geordneten Basen $B = (b_1, \dots, b_m)$ und $B' = (b_1{}', \dots, b_m{}')$ . Dann gilt für die Darstellungsmatrizen von bezüglich und bzw. bezüglich und :

$M_{B'}^{A'}(f)=T_{B'}^{B}\cdot M_{B}^{A}(f)\cdot T_{A}^{A'}$

Man erhält diese Darstellung, indem man

$f = \operatorname{id}_W \circ f \circ \operatorname{id}_V$

schreibt. Die Abbildungsmatrix der Verkettung ist dann das Matrizenprodukt der einzelnen Abbildungsmatrizen, wenn die Basen passend gewählt sind, das heißt: die Basis im Urbild von $\operatorname{id}_V$ , die Basis im Bild von $\operatorname{id}_V$ und im Urbild von , die Basis im Bild von und im Urbild von $\operatorname{id}_W$ , und die Basis im Bild von $\operatorname{id}_W$ . Man erhält also:

$M_{B'}^{A'}(f) = M_{B'}^B(\operatorname{id}_W) \cdot M_B^A(f) \cdot M_A^{A'}(\operatorname{id}_V)$

Ein wichtiger Spezialfall ist, wenn $f \colon V \to V$ ein Endomorphismus ist und im Urbild und Bild jeweils dieselbe Basis bzw. benutzt wird. Dann gilt:

$M_{B'}^{B'}(f)=T_{B'}^B\cdot M_B^B(f)\cdot T_B^{B'}$

Setzt man $T := T_{B'}^B$ , so gilt also

$M_{B'}^{B'}(f) = T \cdot M_B^B(f) \cdot T^{-1}.$

Die Abbildungsmatrizen $M_{B'}^{B'}(f)$ und $M_{B}^{B}(f)$ sind also ähnlich.

Beispiel

Wir betrachten zwei Basen B = (b_1, b_2, b_3) und B' = (b_1', b_2', b_3') des $\mathbb{R}^3$ mit

$b_1 = \begin{pmatrix} 1 \\ 0 \\ 2 \end{pmatrix} , b_2 = \begin{pmatrix} 3 \\ 1 \\ 0 \end{pmatrix} , b_3 = \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}$

und

$b_1' = \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} , b_2' = \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} , b_3' = \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}\,,$

wobei die Koordinatendarstellung der Vektoren die Vektoren bezüglich der Standardbasis beschreibt.

Die Transformation der Koordinaten eines Vektors

ergibt sich durch die Darstellung der alten Basisvektoren $(b_{1},b_{2},b_{3})$ bezüglich der neuen Basis $(b_{1}',b_{2}',b_{3}')$ und deren Gewichtung mit $(x_{1},x_{2},x_{3})$ .

Um die Matrix der Basistransformation $T^B_{B'} = (a_{ij})$ von nach zu berechnen, müssen wir die drei linearen Gleichungssysteme

$x_{j}=a_{1j}x_{1}'+a_{2j}x_{2}'+a_{3j}x_{3}'$

nach den 9 Unbekannten $a_{ij}$ auflösen.

Dies kann mit dem Gauß-Jordan-Algorithmus für alle drei Gleichungssysteme simultan erfolgen. Dazu wird folgendes lineares Gleichungssystem aufgestellt:

$\left({\begin{array}{c c c | c c c}1&0&1&1&3&2\\0&1&1&0&1&1\\1&1&0&2&0&1\end{array}}\right)$

Durch Umformen mit elementaren Zeilenoperationen lässt sich die linke Seite auf die Einheitsmatrix bringen und auf der rechten Seite erhält man als Lösung des Systems die Transformationsmatrix

$T^B_{B'} = \begin{pmatrix} \frac{3}{2} & 1 & 1 \\ \frac{1}{2} & -1 & 0 \\ -\frac{1}{2} & 2 & 1 \end{pmatrix}$ .

Wir betrachten den Vektor v = 2b_1 - b_2 + 3b_3 , also den Vektor der bezüglich der Basis die Koordinaten

$\begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} 2 \\ -1 \\ 3 \end{pmatrix}$

besitzt. Um nun die Koordinaten bezüglich zu berechnen, müssen wir die Transformationsmatrix $T^B_{B'}$ mit diesem Spaltenvektor multiplizieren:

$\begin{pmatrix} x_1' \\ x_2' \\ x_3' \end{pmatrix} = \begin{pmatrix} \frac{3}{2} & 1 & 1 \\ \frac{1}{2} & -1 & 0 \\ -\frac{1}{2} & 2 & 1 \end{pmatrix} \begin{pmatrix} 2 \\ -1 \\ 3 \end{pmatrix} = \begin{pmatrix} 5 \\ 2 \\ 0 \end{pmatrix}$ .

Also ist v = 5b_1' + 2b_2' + 0b_3' .

In der Tat rechnet man als Probe leicht nach, dass

gilt.

Basiswechsel mit Hilfe der dualen Basis

Im wichtigen und anschaulichen Spezialfall des euklidischen Vektorraums (V, ·) kann der Basiswechsel elegant mit der dualen Basis $({\vec {b}}^{1},\ldots ,{\vec {b}}^{n})$ einer Basis $({\vec {b}}_{1},\ldots ,{\vec {b}}_{n})$ durchgeführt werden. Für die Basisvektoren gilt dann

${\vec {b}}_{i}\cdot {\vec {b}}^{j}=\delta _{i}^{j}.$

mit dem Kronecker-Delta $\delta$ . Skalare Multiplikation eines Vektors ${\vec {v}}$ mit den Basisvektoren ${\vec {b}}^{i}$ , Multiplikation dieser Skalarprodukte mit den Basisvektoren ${\vec {b}}_{i}$ und Addition aller Gleichungen ergibt einen Vektor ${\vec {w}}:=({\vec {b}}^{i}\cdot {\vec {v}}){\vec {b}}_{i}.$ Hier wie im Folgenden ist die Einsteinsche Summenkonvention anzuwenden, der zufolge über in einem Produkt doppelt vorkommende Indizes, im vorhergehenden Satz beispielsweise nur , von eins bis zu summieren ist. Skalare Multiplikation von ${\vec {w}}$ mit irgendeinem Basisvektor ${\vec {b}}^{k}$ ergibt wegen

${\vec {w}}\cdot {\vec {b}}^{k}=({\vec {b}}^{i}\cdot {\vec {v}}){\vec {b}}_{i}\cdot {\vec {b}}^{k}=({\vec {b}}^{i}\cdot {\vec {v}})\delta _{i}^{k}={\vec {b}}^{k}\cdot {\vec {v}}$

dasselbe Ergebnis wie die skalare Multiplikation von ${\vec {v}}$ mit diesem Basisvektor, weswegen die beiden Vektoren identisch sind:

${\vec {v}}=({\vec {b}}^{i}\cdot {\vec {v}}){\vec {b}}_{i}=:v^{i}{\vec {b}}_{i}.$

Analog zeigt sich:

${\vec {v}}=({\vec {b}}_{i}\cdot {\vec {v}}){\vec {b}}^{i}=:v_{i}{\vec {b}}^{i}.$

Dieser Zusammenhang zwischen den Basisvektoren und einem Vektor, seinen Komponenten und Koordinaten, gilt für jeden Vektor im gegebenen Vektorraum.

Wechsel zur dualen Basis

Skalare Multiplikation beider Gleichungen mit ${\vec {b}}^{k}$ liefert $v^{i}{\vec {b}}_{i}\cdot {\vec {b}}^{k}=v_{i}{\vec {b}}^{i}\cdot {\vec {b}}^{k}$ oder

$v^{k}=b^{ki}v_{i}.$

Die Umkehroperation mit ${\vec {b}}_{k}$ ist

$v_{k}=v^{i}{\vec {b}}_{i}\cdot {\vec {b}}_{k}=b_{ki}v^{i}.$

Für die oben benutzten Skalarprodukte $b_{ij}:={\vec {b}}_{i}\cdot {\vec {b}}_{j}$ und $b^{kl}:={\vec {b}}^{k}\cdot {\vec {b}}^{l}$ gilt:

$b_{ik}b^{kj}=b^{jk}b_{ki}=({\vec {b}}^{j}\cdot {\vec {b}}^{k})({\vec {b}}_{k}\cdot {\vec {b}}_{i})=[({\vec {b}}^{j}\cdot {\vec {b}}^{k}){\vec {b}}_{k}]\cdot {\vec {b}}_{i}={\vec {b}}^{j}\cdot {\vec {b}}_{i}=\delta _{i}^{j}.$

Wechsel zu einer anderen Basis

Gegeben sei ein Vektor ${\vec {v}}$ , der von einer Basis $({\vec {a}}_{1},\ldots ,{\vec {a}}_{n})$ zur Basis $({\vec {b}}_{1},\ldots ,{\vec {b}}_{n})$ wechseln soll. Das gelingt, indem jeder Basisvektor gemäß ${\vec {a}}_{j}=({\vec {b}}^{i}\cdot {\vec {a}}_{j}){\vec {b}}_{i}$ durch die neue Basis ausgedrückt wird:

${\vec {v}}=x_{j}{\vec {a}}_{j}=x_{j}({\vec {b}}^{i}\cdot {\vec {a}}_{j}){\vec {b}}_{i}=x_{i}^{\prime }{\vec {b}}_{i}$ mit $x_{i}^{\prime }:=({\vec {b}}^{i}\cdot {\vec {a}}_{j})x_{j}.$

Die Umkehrung davon ist $x_{i}:=({\vec {b}}_{i}\cdot {\vec {a}}^{j})x_{j}^{\prime }.$ Der Basiswechsel bei Tensoren zweiter Stufe wird analog durchgeführt:

$\mathbf {M} :=M_{ij}{\vec {a}}_{i}\otimes {\vec {b}}_{j}:=M_{ij}[({\vec {c}}^{k}\cdot {\vec {a}}_{i}){\vec {c}}_{k}]\otimes [({\vec {d}}^{l}\cdot {\vec {b}}_{j}){\vec {d}}_{l}]:=M_{kl}^{\prime }{\vec {c}}_{k}\otimes {\vec {d}}_{l}$ mit $M_{kl}^{\prime }=({\vec {c}}^{k}\cdot {\vec {a}}_{i})M_{ij}({\vec {d}}^{l}\cdot {\vec {b}}_{j})$

was sich ohne weiteres auf Tensoren höherer Stufe verallgemeinern lässt. Das Rechenzeichen „ $\otimes$ “ bildet das dyadische Produkt.

Der Zusammenhang zwischen den Koordinaten

$x_{i}^{\prime }:=({\vec {b}}^{i}\cdot {\vec {a}}_{j})x_{j}$ und $M_{kl}^{\prime }=({\vec {c}}^{k}\cdot {\vec {a}}_{i})M_{ij}({\vec {d}}^{l}\cdot {\vec {b}}_{j})$

kann kompakt mit Basiswechselmatrizen $T_{Q}^{P}$ mit den Komponenten $(T_{Q}^{P})_{ij}={\vec {q}}^{i}\cdot {\vec {p}}_{j}$ bei einem Basiswechsel von $({\vec {p}}_{1},\ldots ,{\vec {p}}_{n})$ nach $({\vec {q}}_{1},\ldots ,{\vec {q}}_{n})$ und ihren dualen Partnern dargestellt werden. Die Inverse der Basiswechselmatrix hat, wie oben angedeutet, die Komponenten $(T_{Q}^{P})_{ij}^{-1}={\vec {p}}^{i}\cdot {\vec {q}}_{j},$ denn bei der Matrizenmultiplikation ergibt sich für Komponenten $ij$ :

$[T_{Q}^{P}\cdot (T_{Q}^{P})^{-1}]_{ij}=({\vec {q}}^{i}\cdot {\vec {p}}_{k})({\vec {p}}^{k}\cdot {\vec {q}}_{j})=[({\vec {q}}^{i}\cdot {\vec {p}}_{k}){\vec {p}}^{k}]\cdot {\vec {q}}_{j}={\vec {q}}^{i}\cdot {\vec {q}}_{j}=\delta _{j}^{i}.$

Anwendungen

Basiswechselmatrizen besitzen vielfältige Anwendungsmöglichkeiten in der Mathematik und Physik.

In der Mathematik

Eine Anwendung von Basiswechselmatrizen in der Mathematik ist die Veränderung der Gestalt der Abbildungsmatrix einer linearen Abbildung, um die Rechnung zu vereinfachen.

Möchte man zum Beispiel die Potenz A^p einer $n\times n$ -Matrix mit einem Exponenten p > 1 berechnen, so ist die Zahl der benötigten Matrizenmultiplikationen von der Größenordnung $O(\log p)$ . Ist diagonalisierbar, so existieren eine Diagonalmatrix und eine Basiswechselmatrix $T \in Gl\left(n,K\right)$ , sodass $A=T\cdot D\cdot T^{-1}$ und somit

$A^p = \left( T \cdot D \cdot T^{-1} \right)^p = T \cdot D^p \cdot T^{-1}$

Die Zahl der für die Berechnung der rechten Seite benötigten Multiplikationen ist nur von der Größenordnung:

$n\log p$ zur Berechnung von ,
$n^{2}$ zur Berechnung des Produkts $D^p\cdot T^{-1}$
sowie einer Matrixmultiplikation für das Produkt $T\cdot(D^p T^{-1})$

Da die Matrixmultiplikation von der Größenordnung $O(n^{{2{,}3727}})$ ist, erhalten wir eine Komplexität von $O(n^{2{,}3727}+n\cdot \log(p))$ anstelle von $O(n^{2{,}3727}\cdot \log(p))$ .

In der Physik

Eine Anwendung von Basiswechselmatrizen in der Physik findet bspw. in der Ähnlichkeitstheorie statt, um dimensionslose Kennzahlen zu ermitteln. Hierbei werden durch einen Basiswechsel einer physikalischen Größe neue Basisdimensionen zugeordnet. Die dimensionslosen Kennzahlen stellen dann genau das Verhältnis der physikalischen Größe zu seiner Dimensionsvorschrift dar.

Literatur

Peter Knabner, Wolf Barth: Lineare Algebra. Grundlagen und Anwendungen. Springer Spektrum, Berlin/Heidelberg 2013, ISBN 978-3-642-32185-6.

Basierend auf einem Artikel in:

Wikipedia.de