Standardbasis

Als Standardbasis, natürliche Basis, Einheitsbasis oder kanonische Basis bezeichnet man im mathematischen Teilgebiet der Linearen Algebra eine spezielle Basis, die in gewissen Vektorräumen bereits aufgrund ihrer Konstruktion unter allen möglichen Basen ausgezeichnet ist.

Basis allgemein

→ Hauptartikel: Basis (Vektorraum)

Allgemein ist eine Basis eines Vektorraums eine Familie von Vektoren mit der Eigenschaft, dass sich jeder Vektor des Raumes eindeutig als endliche Linearkombination dieser darstellen lässt. Die Koeffizienten dieser Linearkombination heißen die Koordinaten des Vektors bezüglich dieser Basis. Ein Element der Basis heißt Basisvektor.

Jeder Vektorraum hat eine Basis, im Allgemeinen sogar zahlreiche Basen, unter denen jedoch keine ausgezeichnet ist.

Beispiele

Die Parallelverschiebungen der Anschauungsebene bilden einen Vektorraum (siehe Euklidischer Raum) der Dimension zwei. Es ist jedoch keine Basis ausgezeichnet. Eine mögliche Basis bestünde etwa aus der „Verschiebung um eine Einheit nach rechts“ und der „Verschiebung um eine Einheit nach oben“. Hierbei sind „Einheit“, „rechts“ und „oben“ aber Konventionen bzw. anschauungsabhängig.
Diejenigen reellwertigen Funktionen $f\colon \R\to\R$ , die zweimal differenzierbar sind und für alle $x\in \mathbb {R}$ die Gleichung erfüllen, bilden einen reellen Vektorraum der Dimension zwei. Eine mögliche Basis wird von der Sinus- sowie der Cosinus-Funktion gebildet. Diese Basis zu wählen, mag zwar naheliegen, sie ist jedoch nicht besonders vor anderen Auswahlen ausgezeichnet.

Standardbasis in den Standardräumen

Standardbasisvektoren in der euklidischen Ebene

Die meist als erstes eingeführten Vektorräume sind die Standardräume $\mathbb {R} ^{n}$ mit $n\in \mathbb {N}$ . Elemente des $\mathbb {R} ^{n}$ sind alle -Tupel reeller Zahlen. Man kann unter allen Basen des $\mathbb {R} ^{n}$ diejenige auszeichnen, bezüglich der die Koordinaten eines Vektors genau mit seinen Tupel-Komponenten übereinstimmen. Diese Basis besteht also aus $e_{1},\ldots ,e_{n}$ wobei

${\begin{matrix}e_{1}&=&(1,0,0,\ldots ,0),\\e_{2}&=&(0,1,0,\ldots ,0),\\&\vdots &\\e_{n}&=&(0,0,0,\ldots ,1)\end{matrix}}$

und wird als die Standardbasis des $\mathbb {R} ^{n}$ bezeichnet.

Dasselbe gilt für den Vektorraum $K^{n}$ über einem beliebigen Körper , das heißt auch hier gibt es die Standard-Basisvektoren $e_{1}=(1,0,\ldots ,0),\ldots ,e_{n}=(0,\ldots ,0,1)$ .

Beispiel

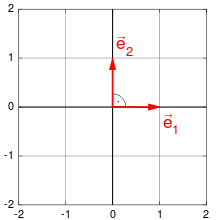
Die Standardbasis des $\mathbb {R} ^{2}$ besteht aus $e_{1}=(1,0)$ und $e_{2}=(0,1)$ . Die beiden oben als Beispiel aufgeführten Vektorräume sind zwar isomorph zu $\mathbb {R} ^{2}$ , besitzen jedoch keine Standardbasis. Infolgedessen ist auch unter den Isomorphismen zwischen diesen Räumen und $\mathbb {R} ^{2}$ keiner ausgezeichnet.

Bezeichnung

Die Bezeichnung $e_{1},e_{2},\ldots$ für die Standard-Basisvektoren ist weit verbreitet. Die drei Standard-Basisvektoren des dreidimensionalen Vektorraums $\mathbb {R} ^{3}$ werden in den angewandten Naturwissenschaften jedoch manchmal mit ${\mathbf {i}},\,{\mathbf {j}},\,{\mathbf {k}}$ bezeichnet:

${\mathbf {i}}=e_{1}={\begin{pmatrix}1\\0\\0\end{pmatrix}},\quad {\mathbf {j}}=e_{2}={\begin{pmatrix}0\\1\\0\end{pmatrix}},\quad {\mathbf {k}}=e_{3}={\begin{pmatrix}0\\0\\1\end{pmatrix}}$

Weitere Eigenschaften

Der $\mathbb {R} ^{n}$ hat über die Vektorraum-Eigenschaft hinaus noch weitere Eigenschaften. Auch hinsichtlich dieser erfüllen die Standard-Basisvektoren oft besondere Bedingungen. So ist die Standardbasis eine Orthonormalbasis bezüglich des Standardskalarprodukts.

Standardbasis im Matrizenraum

Auch die Menge der Matrizen über einem Körper $K^{m\times n}$ bildet mit der Matrizenaddition und der Skalarmultiplikation einen Vektorraum. Die Standardbasis in diesem Matrizenraum wird durch die Standardmatrizen $E_{{ij}}$ gebildet, bei denen genau ein Eintrag gleich eins und alle anderen Einträge gleich null sind. Beispielsweise bilden die vier Matrizen

$E_{{11}}={\begin{pmatrix}1&0\\0&0\end{pmatrix}},E_{{12}}={\begin{pmatrix}0&1\\0&0\end{pmatrix}},E_{{21}}={\begin{pmatrix}0&0\\1&0\end{pmatrix}},E_{{22}}={\begin{pmatrix}0&0\\0&1\end{pmatrix}}$

die Standardbasis des Raums der $(2\times 2)$ -Matrizen.

Standardbasis in unendlichdimensionalen Räumen

Ist ein Körper und eine beliebige (insb. möglicherweise unendliche) Menge, so bilden die endlichen formalen Linearkombinationen von Elementen aus einen Vektorraum. Dann ist selbst Basis dieses Vektorraumes und wird als dessen Standardbasis bezeichnet.

Anstelle formaler Linearkombinationen betrachtet man auch alternativ den Vektorraum derjenigen Abbildungen $f\colon M\to K$ mit der Eigenschaft, dass f(x)=0 für fast alle $x\in M$ gilt. Zu $m\in M$ sei $e_{m}\colon M\to K$ die durch

$e_{m}(x)={\begin{cases}1,&{\text{falls }}x=m\\0,&{\text{falls }}x\neq m\end{cases}}$

gegebene Abbildung $M\to K$ . Dann bildet die Familie $\{e_{m}\}_{{m\in M}}$ eine Basis des Vektorraums, die in diesem Fall ebenfalls als die Standardbasis bezeichnet wird.

Der Vektorraum aller Abbildungen $f\colon M\to K$ besitzt hingegen, sofern unendlich ist, keine Standardbasis.

Auch Polynomringe über Körpern sind Vektorräume, in denen eine Basis bereits unmittelbar aufgrund der Konstruktion ausgezeichnet ist. So sind die Elemente des Polynomringes $\R[X]$ definitionsgemäß die endlichen Linearkombinationen der Monome $X^{2},$ $X^{3}$ usw., die demnach eine Basis – die Standardbasis – von $\R[X]$ bilden.

Zusammenhang mit universellen Eigenschaften

Der Begriff kanonisch wird allgemein bei Konstruktionen über eine universelle Eigenschaft verwendet. So ergibt sich auch ein Zusammenhang zwischen Standardbasen und folgender Konstruktion:

Sei ein Körper und eine beliebige Menge. Gesucht ist ein -Vektorraum zusammen mit einer Abbildung $f\colon M\to U$ in dessen zugrunde liegende Menge, so dass zu jedem -Vektorraum und jeder Abbildung $g\colon M\to X$ genau eine lineare Abbildung $h\colon U\to X$ existiert mit $g=h\circ f$ . In solch einem Paar (U,f) wird dann als kanonische Abbildung oder universelle Lösung von bezüglich des Vergissfunktors, der jedem -Vektorraum die zugrundeliegende Menge zuordnet, bezeichnet.

Die oben angegebenen Vektorräume mit Standardbasis haben genau diese universelle Eigenschaft. Das Bild von unter der kanonischen Abbildung sind genau die Vektoren der kanonischen Basis bzw. die kanonische Abbildung als Familie aufgefasst ist die kanonische Basis.

Daraus, dass stets eine solche universelle Lösung existiert, folgt bereits, dass eine Abbildung, die jeder Menge eine solche universelle Lösung und jedem ein solches zuordnet, ein Funktor ist, der linksadjungiert zum Vergissfunktor ist. Ein solcher Funktor heißt freier Funktor.

Literatur

Kowalsky und Michler: Lineare Algebra, Gruyter, ISBN 978-3110179637.
Albrecht Beutelspacher: „Das ist o.B.d.A. trivial!“ 9. aktualisierte Auflage, Vieweg + Teubner, Braunschweig und Wiesbaden 2009, ISBN 978-3-8348-0771-7, s.v. „Kanonisch“

Basierend auf einem Artikel in:

Wikipedia.de