Lipschitz-Stetigkeit

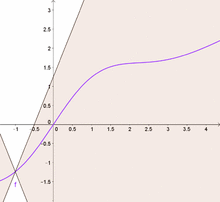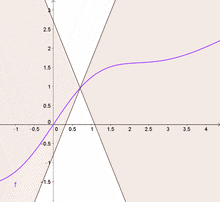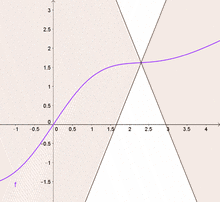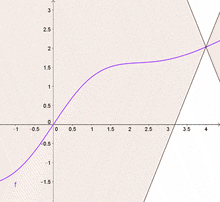
Für eine Lipschitz-stetige Funktion existiert ein Doppelkegel (weiß) dessen Ursprung entlang des Graphs bewegt werden kann, sodass dieser stets außerhalb des Kegels bleibt

Lipschitz-Stetigkeit (nach Rudolf Lipschitz), auch Dehnungsbeschränktheit, bezeichnet in der Analysis eine Verschärfung der Stetigkeit. Anschaulich gesprochen kann eine Lipschitz-stetige Funktion sich nur beschränkt schnell ändern: Alle Sekanten einer Funktion haben eine Steigung, deren Betrag nicht größer ist als eine Konstante, die Lipschitz-Konstante.

Verallgemeinerungen der Lipschitz-Stetigkeit sind die Hölder-Stetigkeit sowie die Lokale Hölder-Stetigkeit.

Definition

Eine Funktion $f\colon\R\rightarrow\R$ heißt Lipschitz-stetig, wenn eine Konstante existiert, so dass

$|f(x_1)-f(x_2)|\le L \cdot |x_1-x_2|$

für alle $x_1, x_2 \in \R$ gilt.

Dies ist ein Spezialfall der folgenden, allgemeinen Definition.

Seien (X,d_X) und (Y,d_Y) metrische Räume. Eine Funktion $f\colon X\rightarrow Y$ heißt Lipschitz-stetig, falls es eine reelle Zahl gibt, sodass

$\forall x_1,x_2 \in X : d_Y(f(x_1),f(x_2)) \le L \cdot d_X(x_1,x_2)$

erfüllt ist. wird Lipschitz-Konstante genannt und es gilt stets $L \geq 0$ . Anschaulich gesprochen ist der Betrag der Steigung von nach oben durch beschränkt. Ist eine Funktion Lipschitz-stetig, so sagt man auch, sie erfülle die Lipschitz-Bedingung.

Eine Abschwächung der Lipschitz-Stetigkeit ist die lokale Lipschitz-Stetigkeit. Eine Funktion $f\colon X\rightarrow Y$ heißt lokal Lipschitz-stetig, wenn es um jeden Punkt in eine Umgebung gibt, sodass die Einschränkung von auf diese Umgebung Lipschitz-stetig ist. Eine Funktion, die nur auf einer Teilmenge $A\subset X$ definiert ist, heißt Lipschitz- oder lokal Lipschitz-stetig, wenn sie Lipschitz- oder lokal Lipschitz-stetig bezüglich der metrischen Räume (A,d_X|A) und (Y,d_Y) ist.

Eigenschaften

Lipschitz-stetige Funktionen sind lokal Lipschitz-stetig (wähle ganz als Umgebung und stets als Lipschitz-Konstante). Lokal Lipschitz-stetige Funktionen sind stetig (wähle $\delta=\varepsilon/ L$ in der $\varepsilon$ - $\delta$ -Definition der Stetigkeit), und entsprechend sind Lipschitz-stetige Funktionen gleichmäßig stetig. Daher ist Lipschitz-Stetigkeit „stärker“ als gleichmäßige Stetigkeit. Die Umkehrung gilt im Allgemeinen nicht, so ist z.B. die Funktion $f\colon[0,1]\rightarrow\R,~x\mapsto\sqrt x$ zwar Hölder-stetig mit Exponenten 1/2 und daher gleichmäßig stetig, jedoch nicht Lipschitz-stetig (siehe Beispiel).

Nach dem Satz von Rademacher ist eine Lipschitz-stetige Funktion fast überall differenzierbar. Es gibt jedoch auch Funktionen, die zwar differenzierbar, aber nicht Lipschitz-stetig sind, z.B. $f\colon\R\rightarrow\R,~x\mapsto x^2$ . Eine differenzierbare Funktion $f\colon (a,b)\rightarrow\R$ mit $a,b\in\R\cup\{\pm\infty\}$ ist genau dann Lipschitz-stetig, wenn ihre erste Ableitung beschränkt ist.

Anwendung

Lipschitz-Stetigkeit ist ein wichtiges Konzept in der Theorie gewöhnlicher Differentialgleichungen, um Existenz und Eindeutigkeit von Lösungen zu beweisen (siehe Satz von Picard-Lindelöf). Abbildungen mit einer Lipschitz-Konstante kleiner als eins nennt man Kontraktionen. Diese sind wichtig für den Fixpunktsatz von Banach.

Menge Lipschitz-stetiger Funktionen

Ist $X\subseteq {\mathbb {R}}$ (oder allgemeiner $\left(X,\,d_{X}\right)$ ein metrischer Raum), so wird die Menge der reellwertigen Lipschitz-stetigen Funktionen auf gelegentlich mit ${\mathrm {Lip}}\left(X\right)$ bezeichnet.

Für $X\subseteq {\mathbb {R}}$ (oder allgemeiner für $X\subseteq {\mathbb {R}}^{n}$ mit der euklidischen Metrik) ist jede affin-lineare Funktion Lipschitz-stetig. Auf einem allgemeinen metrischen Raum sind immerhin alle konstanten Funktionen Lipschitz-stetig. Insbesondere ist ${\mathrm {Lip}}\left(X\right)$ nicht leer und enthält die konstante Nullfunktion.

Sind $f,\,g\in {\mathrm {Lip}}\left(X\right)$ und $\lambda \in \mathbb {R}$ , so gilt $\lambda \,f\in {\mathrm {Lip}}\left(X\right)$ sowie $f+g\in {\mathrm {Lip}}\left(X\right)$ . Damit ist ${\mathrm {Lip}}\left(X\right)$ ein reeller Vektorraum, ein Funktionenraum.

Ist die Menge zudem noch beschränkt, so gilt außerdem für das punktweise Produkt $f\cdot g\in {\mathrm {Lip}}\left(X\right)$ . Damit wird ${\mathrm {Lip}}\left(X\right)$ zu einer Funktionenalgebra.

Beispiele

Für eine Lipschitz-stetige Funktion $f\colon(X,d_X)\rightarrow (Y,d_Y)$ ist der Quotient

$\frac{d_Y(f(x_1),f(x_2))}{d_X(x_1,x_2)}$

mit $x_1\neq x_2 \in X$ durch jede Lipschitz-Konstante von nach oben beschränkt. Für lokal Lipschitz-stetige Funktionen ist der Quotient auf hinreichend kleinen Umgebungen beschränkt.

Daher ist die Funktion $f\colon [0,1]\to\R$ mit $x\mapsto\sqrt x$ wegen

$\frac{|f(x_1)-f(0)|}{|x_1-0|}=\frac 1{\sqrt x_1}\xrightarrow{x_1\searrow 0}\infty$

zwar stetig und sogar gleichmäßig stetig, jedoch nicht lokal Lipschitz-stetig und folglich auch nicht Lipschitz-stetig.

Für die Funktion $g\colon[a,b]\to\R$ mit $x\mapsto x^2$ folgt mit

$L:=\max_{x_1,x_2 \in [a,b]}(|x_1+x_2|)=2\max{(|a|,|b|)},$

dass

$|g(x_1)-g(x_2)|=|x_1^2-x_2^2|=|x_1+x_2|\cdot|x_1-x_2|\leq L\cdot |x_1-x_2|.$

Das heißt, ist eine Lipschitz-Konstante für diese Funktion auf dem Intervall $\left[a,b\right]$ .

Weil für der Quotient gleich |x_1+x_2| ist, folgt, dass nur für einen beschränkten Definitionsbereich Lipschitz-stetig ist, für einen unbeschränkten jedoch nicht. Die ebenfalls durch g(x)=x^2 definierte Funktion $g\colon\R\to\R$ ist deshalb nicht Lipschitz-stetig.

Die Betragsfunktion $h\colon \mathbb{R} \rightarrow \mathbb{R}$ , definiert als

ist wegen der umgekehrten Dreiecksungleichung $\bigl||x_1|-|x_2|\bigr| \leq |x_1-x_2|$ Lipschitz-stetig mit L = 1 , aber sie ist (an der Stelle x=0 ) nicht differenzierbar.

Basierend auf einem Artikel in:

Wikipedia.de