
Gleichmäßige Stetigkeit
Die Gleichmäßige Stetigkeit ist eine stärkere Form der Stetigkeit und damit ein Begriff der Analysis. Bei einer gleichmäßig stetigen Funktion ist der Abstand beliebiger Paare von Funktionswerten kleiner als ein beliebig vorgegebener Maximalfehler, solange die Argumente hinreichend nah beieinanderliegen.
Definition
Sei
eine Teilmenge von
,
kurz
.
Eine Abbildung
heißt gleichmäßig stetig genau dann, wenn
.
Zur besseren Unterscheidung bezeichnet man die gewöhnliche Stetigkeit, wenn sie in
jedem Punkt von
gegeben ist, auch als punktweise Stetigkeit.
Die Besonderheit der gleichmäßigen Stetigkeit besteht darin, dass
nur von
und nicht, wie bei der punktweisen Stetigkeit, noch zusätzlich von der Stelle
abhängt.
Anschaulich bedeutet das: Zu jeder noch so kleinen senkrechten Rechteckseite
kann man eine hinreichend kleine waagrechte Rechteckseite
finden, sodass, wenn man das Rechteck mit den Seiten
geeignet auf dem Funktionsgraphen entlangführt, dieser immer nur die senkrechten
Rechtecksseiten schneidet. (Bsp.: Wurzelfunktion auf
).
Beispiele
Betrachte die Funktion
mit
:
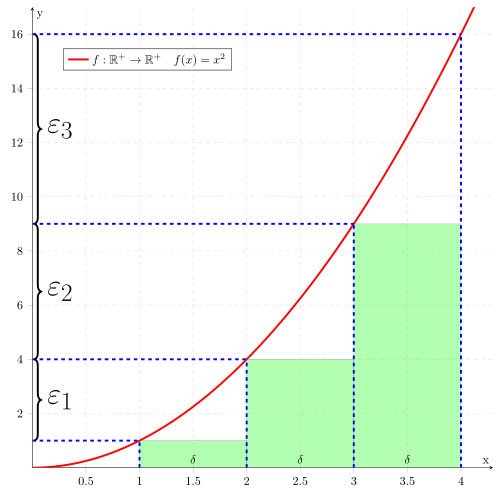
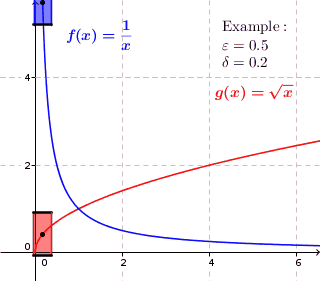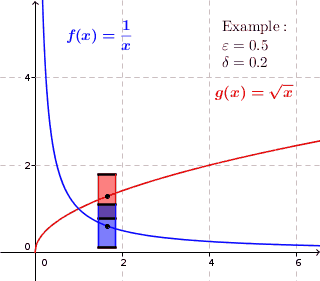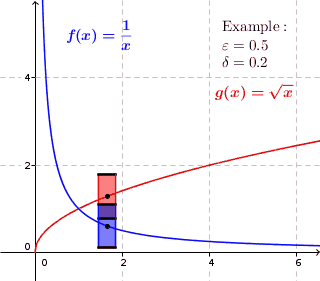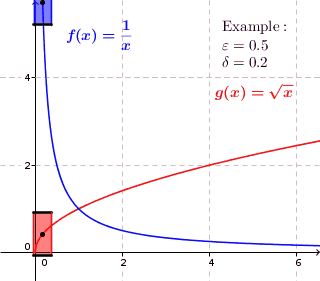
Diese ist stetig, aber nicht gleichmäßig stetig: Je weiter rechts man in
einem der -Streifen
zwei Punkte wählt, desto größer kann der Abstand der beiden Funktionswerte
werden und somit unser gewähltes
übersteigen. Dies entspricht nicht der Definition gleichmäßiger Stetigkeit: Der
Abstand der Funktionswerte muss für jede Wahl zweier solcher Stellen kleiner als
ein vorgegebenes
sein. Das ist bei dieser Funktion nicht der Fall.
Weiterhin gilt: Jede Einschränkung von
auf ein kompaktes Intervall ist gleichmäßig stetig. Dies folgt unmittelbar aus
dem Satz
von Heine.
Ein anderes Beispiel ist die stetige Funktion
mit
die gleichmäßig stetig, sogar hölderstetig, aber nicht lipschitzstetig ist.
Verallgemeinerung: metrische Räume
Allgemeiner wird auch folgende Definition verwendet:
Seien
zwei metrische Räume. Eine Abbildung
heißt gleichmäßig stetig genau dann, wenn
.
Verallgemeinerung: uniforme Räume
Noch allgemeiner heißt in der Topologie
eine Funktion
zwischen zwei uniformen
Räumen
und
gleichmäßig stetig, wenn das Urbild jeder Nachbarschaft
wieder eine Nachbarschaft ist, wenn also
Eigenschaften
Jede gleichmäßig stetige Funktion ist stetig. Die Umkehrung gilt nicht: Es gibt stetige Funktionen wie die Quadratfunktion, die nicht gleichmäßig stetig sind. Für gewisse Definitionsbereiche fallen Stetigkeit und gleichmäßige Stetigkeit wiederum zusammen. Der Satz von Heine besagt nämlich: Jede stetige Funktion auf einer kompakten Menge ist gleichmäßig stetig.
Ist
eine Cauchy-Folge im Raum
und ist
gleichmäßig stetig, so ist auch
eine Cauchy-Folge in
.
Dies gilt im Allgemeinen nicht für Funktionen, die nur stetig sind, wie das
Beispiel
und
zeigt.
Unmittelbar daraus, dass
Cauchy-Folgen auf Cauchy-Folgen abbildet, folgt nun: Ist
gleichmäßig stetig auf einer Menge
,
dann ist
stetig fortsetzbar auf den Abschluss
.
Im
lässt sich anschaulich die Aussage treffen, dass eine gleichmäßig stetige
Funktion (mit Werten in
)
keine Polstellen besitzen kann. Wie sollte sie auch, lässt sie sich doch –
wie bereits dargestellt – stetig auf den Abschluss ihres
Definitionsbereiches fortsetzen. Eine solche stetige Fortsetzung ist in einer
Polstelle aber eben nicht möglich.
Spezielle Formen der gleichmäßigen Stetigkeit sind Hölder- und Lipschitz-Stetigkeit.
Visualisierung
Bei einer gleichmäßig stetigen Funktion kann für jeden vorgegebenen
Maximalfehler
ein
gefunden werden, so dass sich alle Paare von Funktionswerten
und
um maximal
unterscheiden, solange die Abstände von
und
kleiner als
sind. Dementsprechend kann um jeden Punkt
des Graphen ein Rechteck mit Höhe
und Breite
eingezeichnet werden, bei dem der Graph komplett im Inneren des Rechtecks
verläuft, so dass keine Funktionswerte direkt ober- beziehungsweise unterhalb
des Rechtecks liegen. Bei nicht gleichmäßig stetigen Funktionen ist dies nicht
möglich. Zum Teil verläuft zwar der Graph im Inneren des Rechtecks – aber nicht
überall.
-
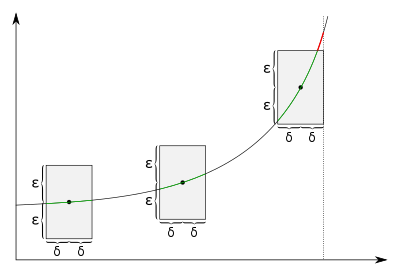
 Bei gleichmäßig stetigen Funktion kann für jedes
Bei gleichmäßig stetigen Funktion kann für jedesum jeden Punkt ein Rechteck mit Höhe
und Breite
eingezeichnet werden, bei dem der Graph komplett im Inneren des Rechtecks verläuft.
-
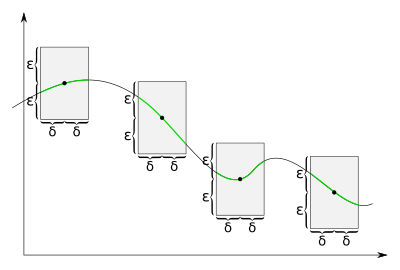
 Bei nicht gleichmäßig stetigen Funktion gibt es Werte
Bei nicht gleichmäßig stetigen Funktion gibt es Wertebei denen es unmöglich ist, ein
zu finden, so dass der Graph überall im Inneren des
-
-Rechtecks verläuft. Wenn man das Rechteck entlang des Graphen verschiebt, so gibt es Stellen, wo Funktionswerte direkt ober- beziehungsweise unterhalb liegen.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 28.06. 2020