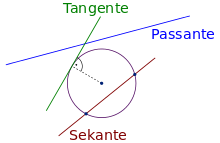
Sekante

Das Wort Sekante (lateinisch: secare = „schneiden“) bezeichnet in der ebenen Geometrie und in der Analysis eine Gerade, die durch zwei Punkte einer Kurve geht.

Kreissekante

Drei Lagen von Geraden zu einem Kreis: Sekante, Tangente, Passante

In der Elementargeometrie versteht man unter einer Sekante eine Gerade, die einen Kreis in zwei Punkten schneidet. Eine Gerade, die genau einen Punkt mit dem Kreis gemeinsam hat, heißt Tangente; eine Gerade, die keinen gemeinsamen Punkt mit dem Kreis hat, heißt Passante. Eine Sekante, die durch den Mittelpunkt des Kreises geht, wird als Zentrale bezeichnet.

Eine Gerade ist genau dann Sekante eines gegebenen Kreises, wenn der Abstand des Kreismittelpunkts von der Geraden kleiner ist als der Radius des Kreises. Ist der Abstand gleich dem Radius, so handelt es sich um eine Tangente; ist er größer als der Radius, so handelt es sich um eine Passante.

Der Abschnitt der Sekante, der innerhalb des Kreises liegt, heißt Sehne. Die längsten Sehnen eines Kreises sind diejenigen, die durch den Kreismittelpunkt gehen. Diese und auch ihre Längen werden als Durchmesser des Kreises bezeichnet.

Der Sekantensatz beschreibt die Beziehung der Abschnittslängen zweier Kreissekanten, die sich außerhalb des Kreises schneiden, der Sekanten-Tangenten-Satz die Beziehung zwischen sich schneidender Tangente und Sekante.

Kurvensekante

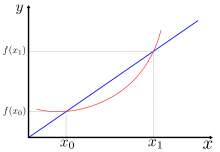
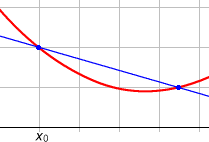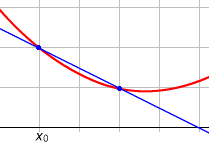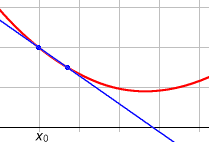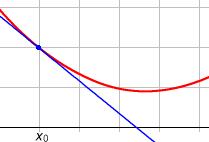
Sekante durch zwei Punkte eines Funktionsgraphen

Für x₁ gegen x₀ nähert sich die Sekante der Tangente bei x₀

Allgemeiner nennt man auch eine Gerade, die durch (mindestens) zwei Punkte einer Kurve, beispielsweise eines Funktionsgraphen, verläuft, eine Sekante. Ihre Steigung heißt Sekantensteigung. Die Steigung der Sekante durch zwei Punkte $(x_{0}|f(x_{0}))$ und $(x_{1}|f(x_{1}))$ des Graphen der Funktion ist gegeben durch

$m_{{{\text{S}}}}={\frac {f(x_{1})-f(x_{0})}{x_{1}-x_{0}}}$ .

Dies ist gerade der Differenzenquotient der Funktion im Intervall $[x_{0},x_{1}]$ . Er spielt eine wichtige Rolle in der Differentialrechnung bei der Definition der Ableitung: Hält man die Stelle $x_{0}$ fest und lässt die Stelle $x_{1}$ gegen $x_{0}$ „wandern“, so nähert sich bei einer differenzierbaren Funktion die Sekante durch die Punkte $(x_{0}|f(x_{0}))$ und $(x_{1}|f(x_{1}))$ der Tangente an den Funktionsgraph im Punkt $(x_{0}|f(x_{0}))$ . Die Sekantensteigung konvergiert dabei gegen die Steigung der Tangente, das ist die Ableitung $f'(x_{0})$ der Funktion an der Stelle $x_{0}$ .

Das Sekantenverfahren ist ein numerisches Näherungsverfahren zur Bestimmung einer Nullstelle mithilfe von Kurvensekanten.

Basierend auf einem Artikel in:

Wikipedia.de