Sekanten-Tangenten-Satz

Sehnentangentenwinkelsatz

$\Rightarrow$

$\angle PG_{2}T=\angle PTG_{1}$

$\Rightarrow$

$\triangle PTG_{2}\sim \triangle PG_{1}T$

$\Rightarrow$

${\frac {|PT|}{|PG_{2}|}}={\frac {|PG_{1}|}{|PT|}}$

$\Rightarrow$

$|PT|^{2}=|PG_{1}|\cdot |PG_{2}|$

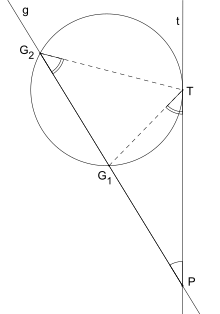
Der Sekanten-Tangenten-Satz (auch Sehnen-Tangenten-Satz genannt) ist ein Lehrsatz der euklidischen Geometrie. Er beschreibt, in welcher Beziehung Strecken stehen, die von einer Tangente, einer Sekante und dem zugehörigen Kreis gebildet werden (siehe Zeichnung).

Gegeben sei ein Kreis mit einer Sekante und einer Tangente , die sich in einem Punkt außerhalb des Kreises schneiden. Bezeichnet man die Schnittpunkte des Kreises mit als $G_{1}$ beziehungsweise $G_{2}$ und den Berührungspunkt der Tangente als , so gilt:

${\overline {PG_{1}}}\cdot {\overline {PG_{2}}}={\overline {PT}}^{2}$

Diese Aussage kann man auch als Verhältnisgleichung formulieren:

${\overline {PG_{1}}}:{\overline {PT}}={\overline {PT}}:{\overline {PG_{2}}}$

Der Sekanten-Tangenten-Satz beschreibt einen Spezialfall des Sekantensatzes, bei dem die Schnittpunkte der zweiten Sekante mit dem Kreis in einem Punkt zusammenfallen. Die Sätze lassen sich – auch ähnlich wie der Sehnensatz – mit Hilfe ähnlicher Dreiecke beweisen. Alle drei Sätze lassen sich mit Hilfe des Begriffes der Potenz zusammenfassen beziehungsweise zu einer einzelnen Aussage vereinheitlichen. Ein rechnerischer Nachweis hierfür mit Hilfe des Satzes von Vieta ist in dem Artikel über die Potenz enthalten.

Literatur

Max Koecher, Aloys Krieg: Ebene Geometrie. 2. Auflage. Springer-Verlag Berlin Heidelberg New York, 2000, ISBN 3-540-67643-0.
H. Schupp: Elementargeometrie, UTB Schöningh (1977), ISBN 3-506-99189-2.
Schülerduden – Mathematik I. Bibliographisches Institut & F.A. Brockhaus, 8. Auflage, Mannheim 2008, ISBN 978-3-411-04208-.

Basierend auf einem Artikel in:

Wikipedia.de