Faserbündel
In der algebraischen Topologie, einem Teilgebiet der Mathematik, ist ein Faserbündel ein topologischer Raum, der lokal als kartesisches Produkt zweier topologischer Räume dargestellt werden kann, zusammen mit einer Abbildung, die diese Ähnlichkeit wiedergibt.
Faserbündel spielen eine wichtige Rolle in der Homotopietheorie, Differentialgeometrie und Differentialtopologie.
Geschichte
Das Konzept eines Faserbündels kam erstmals im Zusammenhang mit der Topologie und Geometrie von Mannigfaltigkeiten auf. Herbert Seifert führte im Jahr 1933 die Begriffe Faser und gefaserter Raum ein.
Die erste Definition eines Faserbündels gab Hassler Whitney im Jahr 1935 unter dem Namen Sphären-Raum (engl. sphere space). In den Jahren von 1935 bis 1940 wurden Faserbündel in der Mathematik ein eigenes Forschungsgebiet. Die Arbeiten von Whitney, Heinz Hopf und Eduard Stiefel gaben Ausblicke auf die Bedeutung von Faserbündeln in Topologie und Differentialgeometrie.
Bis zum Jahr 1950 wurde die Definition eines Faserbündels klar notiert und die Theorie über Homotopieklassifikation und Charakteristikklassen von Faserbündeln von mehreren Mathematikern, darunter Shiing-Shen Chern, Lew Pontrjagin, Stiefel und Whitney, vorangetrieben. In den Jahren von 1950 bis 1955 konnte Friedrich Hirzebruch unter Verwendung der Charakteristikklassen von Faserbündeln den Satz von Hirzebruch-Riemann-Roch beweisen. John Milnor gab eine Konstruktion eines universellen Faserbündels für beliebige topologische Gruppen im Jahr 1955 an. In den frühen 1960er entwickelten Alexander Grothendieck, Michael Atiyah und Hirzebruch eine verallgemeinerte Kohomologietheorie, die K-Theorie, mit Hilfe von Stabilitätsklassen von Vektorbündeln.
Definition
Ein Faserbündel ist ein Quadrupel
bestehend aus topologischen Räumen
,
und
und einer stetigen
surjektiven
Abbildung
,
wobei für jedes
eine offene Umgebung
von
und ein Homöomorphismus
existieren, sodass das folgende Diagramm kommutiert:
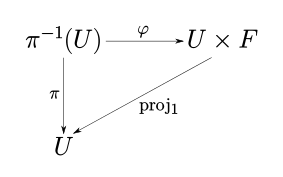
Hierbei ist
die natürliche Projektion. Ein solcher Homöomorphismus
wird lokale Trivialisierung des Bündels und die Abbildung
Projektion genannt. Der Raum
heißt der Basisraum des Bündels,
der Totalraum und
die Faser.
Der Raum
ist mit der Produkttopologie
versehen und
mit der Teilraumtopologie.
Um zusätzlich die Faser des Bündels zu nennen, wird auch die Notation
für ein Faserbündel verwendet. Hierbei ist die Abbildung
die Inklusion
und
wird mit
,
der Faser über einem Punkt
,
identifiziert.
Jedes Faserbündel ist eine Serre-Faserung.
Beispiele
Triviales Bündel
Sei
und
die Projektion auf den ersten Faktor, dann ist
nicht nur lokal ein Produkt, sondern auch global. Ein solches Faserbündel heißt
triviales Bündel oder Produktbündel.
Überlagerung
Ein Faserbündel mit diskreter Faser ist eine Überlagerung. Ebenso ist jede Überlagerung, deren Fasern alle die gleiche Kardinalität haben, ein Faserbündel mit diskreter Faser. Insbesondere ist eine Überlagerung über einem zusammenhängenden Basisraum ein Faserbündel.
Möbiusband

Das Möbiusband
ist ein anschauliches Beispiel für ein nichttriviales Faserbündel. Der Basisraum
ist die Kreislinie ,
die mittig des Bandes verläuft. Die Faser ist durch ein abgeschlossenes
Intervall gegeben, z.B.
Der Totalraum ist gegeben durch den Quotientenraum
mit der Äquivalenzrelation
gegeben durch
Die Bündel-Projektion
ist die von der Projektion
induzierten Abbildung, d.h. eine Äquivalenzklasse
wird unter der Bündel-Projektion auf die Äquivalenzklasse
abgebildet, wobei die Äquivalenzrelation auf
durch
gegeben ist.
Das entsprechende triviale Bündel
ist ein Zylinder.
Möbiusband und Zylinder unterscheiden sich durch eine Verdrehung der Faser.
Diese Verdrehung ist nur global sichtbar, lokal sind Möbiusband und Zylinder
identisch.
Kleinsche Flasche
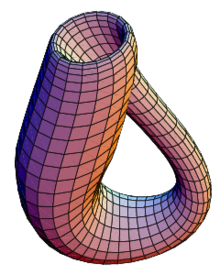
Ein weiteres nichttriviales Faserbündel ist die Kleinsche Flasche.
Der Basisraum und die Faser sind durch
und der Totalraum durch den Quotientenraum
gegeben, wobei die Äquivalenzrelation
durch
und
gegeben ist. Die Bündel-Projektion
bildet ein Element
auf
mit der Äquivalenzrelation
auf
ab.
Das entsprechende triviale Bündel
ist ein Torus,
der lokal von der Kleinschen Flasche nicht unterscheidbar ist.
Hopf-Bündel
Das Hopf-Bündel
hat als Faser, Totalraum und Basisraum Sphären und ist eines der ersten
entdeckten nicht trivialen Faserbündel. Es ist ein Spezialfall für
des Faserbündels
über dem
-dimensionalen
komplexen projektiven Raum.
Weitere Hopf-Bündel, auch verallgemeinerte Hopf-Bündel genannt, lassen sich
durch Ersetzen der komplexen Zahlen mit den reellen
Zahlen, den Quaternionen
und den Oktionen
herleiten:
- Die Überlagerung
über dem
-dimensionalen projektiven Raum ergibt für
das reelle Hopf-Bündel
- Für die Quaternionen ergibt sich das Hopf-Bündel
- Für die Oktionen ergibt sich das Hopf-Bündel
Weitere Faserbündel, deren Faser, Totalraum und Basisraum Sphären sind, existieren nicht. Dies ist eine Folgerung aus dem Satz von Adam, welcher das Problem von H. Hopf über die Anzahl der Abbildungen zwischen Sphären mit Hopf-Invariante 1 löst.
Schnitte
Der Schnitt eines Faserbündels
ist eine stetige Abbildung
die zur Projektion
rechtsinvers ist. Für alle
gilt, dass die Verknüpfung von Projektion und Schnitt gleich der Identität ist:
Anders ausgedrückt liegt für alle
das Bild des Schnitts in der Faser über
Ein lokaler Schnitt eines Faserbündels ist eine stetige Abbildung
wobei
eine offene Teilmenge ist und
für alle
gilt.
Bündelmorphismus
Ein Bündelmorphismus (auch Bündelabbildung genannt) zwischen zwei
Faserbündeln
und
ist eine Abbildung, die die Bündelstruktur erhält; in gewissem Sinne ist es eine
Faser-erhaltende Abbildung. Genauer ist ein Bündelmorphismus durch ein Tupel
von zwei Abbildungen
und
gegeben, sodass
gilt. Die Situation wird durch das folgende kommutative Diagramm verdeutlicht:
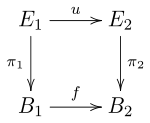
Eine Faser über
wird unter
auf eine Faser über
abgebildet; dies wird durch die Beziehung
dargestellt.
Sind die Basisräume identisch, so ist der Bündelmorphismus durch
gegeben und man spricht von einem
-Morphismus
oder einem Bündelmorphismus über
,
wobei
gilt. Die Beziehung
ist durch das folgende Diagramm gegeben:
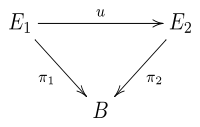
Für alle
gilt die Bedingung
weshalb
auch Faser-erhaltend genannt wird.
Koordinatenbündel
Für jeden Basisraum eines Faserbündels existiert ein Atlas
von Karten, wobei
offene Teilmengen und
lokale Trivialisierungen des Faserbündels sind. Zwei Karten
und
können mittels stetiger Kartenwechsel
gewechselt werden. Die Kartenwechsel geben Auskunft darüber, welche Symmetrien
der Fasern beim Übergang benutzt werden, weshalb sie auch Übergangsfunktionen
genannt werden. Für ein Punkt
ist die Übergangsfunktion durch den Ausdruck
gegeben. Das folgende Diagramm verdeutlicht die Situation:
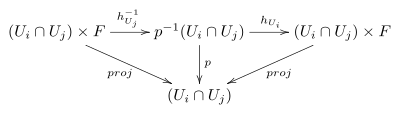
In der ersten Zeile ist die erste Komponente durch die Identität und die zweite Komponente durch die Übergangsfunktion gegeben.
Eine topologische Transformationsgruppe
eines topologischen Raumes
relativ zu einer Abbildung
ist eine topologische Gruppe
sodass:
stetig ist
wobei
die Identität von
ist und
für alle
und
Oft betrachtet man mehr als nur eine solche Abbildung
und ersetzt deshalb
durch
Ein Koordinatenbündel ist ein Faserbündel zusammen mit einer
effektiven topologischen Transformationsgruppe
sodass die folgenden zwei Bedingungen gelten:
- Für jedes
und
entspricht der Homöomorphismus
der Operation eines Gruppenelements in
- für jedes
ist die Abbildung
mit
stetig.
Die Abbildungen
heißen Koordinaten-Übergangsfunktionen (teilweise auch nur
Übergangsfunktionen genannt)
und
heißt die Strukturgruppe des Bündels. Die Koordinaten-Überangsfunktionen
haben die folgenden drei Eigenschaften:
für jedes
und jedes
für jedes
für jedes
Zwei Koordinatenbündel mit selbem Basisraum und Totalraum, gleicher Faser,
Projektion und Strukturgruppe heißen äquivalent, wenn die Atlanten
und
für zwei Indexmengen
und
die folgenden zwei Bedingungen erfüllen:
- Für jedes
stimmt
mit der Operation eines Gruppenelements überein und
- die so definierten Koordinaten-Übergangsfunktionen
sind stetig.
Ein -Faserbündel
ist eine Äquivalenzklasse von Koordinatenbündeln. Häufig wird ein
-Faserbündel
auch als maximales Koordinatenbündel definiert.
Der Bündelkonstruktionssatz liefert Bedingungen, unter welchen die Existenz eines Koordinatenbündels garantiert ist:
Für jede topologische Transformationsgruppe
von einem Raum
und System von Übergangsfunktionen in einem Raum
,
das heißt eine Überdeckung
und eine Menge
von stetigen Abbildungen mit den drei oben genannten Eigenschaften für
Koordinaten-Übergangsfunktionen, existiert ein Koordinatenbündel mit Basisraum
Faser
Strukturgruppe
und Übergangsfunktionen
Hauptfaserbündel
Ein -Hauptfaserbündel
ist ein Faserbündel
mit Faser
und einer Strukturgruppe
die auf der Faser durch Linksmultiplikation operiert. Die Strukturgruppe
operiert frei auf dem Totalraum durch Rechtsmultiplikation mit Bahnenraum
Eine offene Überdeckung
von
wird abzählbar genannt, falls eine lokal endliche Zerlegung der Eins
existiert:
mit
für jedes
Ein -Hauptfaserbündel
heißt abzählbar, falls eine abzählbare Überdeckung
von
existiert, sodass die eingeschränkten Bündel
für jedes
triviale Bündel sind. Ein abzählbares
-Hauptfaserbündel
heißt universelles
Bündel, falls für jeden Raum
die Abbildung
von der Menge der Homotopieklassen von Abbildungen von
nach
in die Menge der Isomorphieklassen von
-Hauptfaserbündeln
eine Bijektion ist. Bei einem universellen Bündel
wird der Basisraum klassifizierender
Raum von
genannt.
Hauptfaserbündel spielen eine wichtige Rolle bei der Klassifikation von
Bündeln. Zudem kann jedes -Faserbündel
mit einem Hauptfaserbündel assoziiert werden und umgekehrt jedes
Hauptfaserbündel mit einem
-Faserbündel.
Assoziierte Hauptfaserbündel
Für ein gegebenes -Faserbündel
lässt sich ein
-Hauptfaserbündel
konstruieren. Die Existenz ist durch den Bündelkonstruktionssatz gegeben, wobei
die Faser als
gewählt wird und
zusätzlich auf sich selbst durch Linksmultiplikation operiert. Der Basisraum und
das System von Übergangsfunktionen werden identisch mit denen des
-Faserbündels
gewählt.
Assoziierte G-Faserbündel
Für ein gegebenes -Hauptfaserbündel
und einen links
-Raum
lässt sich ein
-Faserbündel
konstruieren:
Auf dem Produktraum
ist eine rechts
-Raum
Struktur durch
definiert. Das
-Faserbündel
ist durch die Abbildung
mit
und der Faser
gegeben.
Vektorbündel
Ein Vektorbündel vom Rang
über einem Körper
ist ein Faserbündel
dessen Fasern die Struktur eines
-dimensionalen
-Vektorraumes haben und
zusätzlich jede lokale Trivialisierung
für ein
einen
-linearen
Isomorphismus auf den
einzelnen Fasern induziert. Das bedeutet, dass die Abbildung
eingeschränkt auf ein
ein Isomorphismus ist und somit
gilt. Häufig betrachtet man reelle oder komplexe Vektorbündel, bei denen der
Körper
durch die reellen
Zahlen
bzw. durch die komplexen
Zahlen
gegeben sind.
Es gibt eine natürliche Bijektion zwischen den Isomorphieklassen von
Vektorbündeln mit Rang
von parakompakten
Räumen
und der Menge der Homotopieklassen von Abbildungen von
in die Graßmann-Mannigfaltigkeit
von
-dimensionalen
Unterräumen in
Beispiele
- Das Tangentialbündel
der
mit Totalraum
und Projektion
ist ein Vektorbündel mit Fasern
für jedes
- Das kanonische Vektorbündel
mit Rang
der Graßmann-Mannigfaltigkeit
ist durch den Totalraum
und die Projektion
gegeben.
Sphärenbündel
Ein -Sphärenbündel
ist ein Faserbündel
mit der
-Sphäre
als Faser. Oft ist ein Sphärenbündel zusammen der orthogonalen Gruppe
als Strukturgruppe gegeben.
Ein Sphärenbündel wird orientierbar genannt, falls die Strukturgruppe durch die Drehgruppe gegeben ist.
Die Kohomologie von Sphärenbündel kann mittels der Gysin-Sequenz berechnet werden.
Kohomologie von Faserbündeln
Die Bestimmung der Kohomologiegruppen von Faserbündeln ist deutlich schwieriger, als die Bestimmung der Homotopiegruppen. Die Homotopiegruppen sind durch eine lange exakte Sequenz gegeben, die Kohomologiegruppen haben dagegen nur unter bestimmten Voraussetzungen eine lange exakte Sequenz.
Für ein triviales Bündel ist die Beziehung der Kohomologiegruppen durch die Künneth-Formel gegeben. Für beliebige Faserbündel werden Hilfsmittel, wie Spektralsequenzen benötigt.
Der Satz von Leray-Hirsch liefert ausreichende Bedingungen an ein Faserbündel, sodass die Struktur der Kohomologiegruppen der eines trivialen Bündels sehr ähnlich ist.
Für -Sphärenbündel
die zusätzlich eine Orientierbarkeitsbedingung erfüllen, existiert eine lange
exakte Sequenz von Kohomologiegruppen. Die Sequenz ist unter dem Namen
Gysin-Sequenz
bekannt:
Hierbei ist
eine bestimmte Eulerklasse
in
Beispiele
- Das Hopf-Bündel
hat nicht die Kohomologiestruktur eines trivialen Bündels, da
gilt.
- Für das Faserbündel
gilt:


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 03.04. 2023