Kommutatives Diagramm

In der Mathematik beschreibt ein kommutatives Diagramm, dass verschiedene Verkettungen von Abbildungen das gleiche Ergebnis liefern.

Eine Abbildung von nach kann durch einen Pfeil dargestellt werden.

Die Verkettung mit einer weiteren Abbildung von nach kann durch das Aneinanderhängen der Pfeile ausgedrückt werden. Eine solche Verkettung von Pfeilen nennt sich Diagramm.

Will man dieser Verkettung einen Namen geben, so kann man einen weiteren Pfeil von nach einzeichnen.

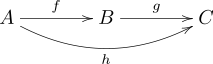
Es wäre denkbar, dass eine beliebige Abbildung von nach ist. Wenn sie mit der Verkettung $g\circ f$ übereinstimmt, sagt man, dass das Diagramm kommutiert.

Allgemein müssen, damit ein Diagramm kommutiert, für alle Wege von nach die Verkettungen der zugehörigen Abbildungen übereinstimmen.

Kurzgefasst: Ein Diagramm kommutiert, „wenn es egal ist, welchen Weg man wählt“.

Beispiele

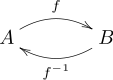
Dieses Diagramm kommutiert genau dann, wenn $f^{{-1}}\circ f={\mathrm {id}}$ und $f\circ f^{{-1}}={\mathrm {id}}$ gilt. Das sind genau die Bedingungen, dafür dass $f^{-1}$ die zu inverse Abbildung ist.

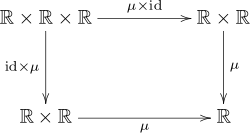
$\mu$ bezeichnet in diesem Diagramm die Multiplikation, das heißt $\mu (x,y)=xy$ . Das Diagramm kommutiert somit genau dann, wenn x(yz)=(xy)z gilt, es drückt also das Assoziativgesetz der Multiplikation reeller Zahlen aus.

Diagrammjagd

Die Diagrammjagd ist ein Beweisverfahren, das besonders in der homologischen Algebra verwendet wird. Anhand eines gegebenen kommutativen Diagrammes werden formale Eigenschaften von Abbildungen (beispielsweise Injektivität, Surjektivität oder Exaktheit) benutzt. Man „jagt“ hierbei Elemente der Objekte auf verschiedenen Wegen durch das Diagramm und vergleicht die erzielten Resultate. Das Diagramm dient dabei lediglich als Hilfsmittel der Visualisierung eines formal auch ohne dieses gültigen Beweises.

Beispiele für Diagrammjagden sind die üblichen Beweise des Fünferlemmas des Schlangenlemmas, des Zick-Zack-Lemmas oder des Neunerlemmas.

Man beachte, dass ein Beweis durch Diagrammjagd unmittelbar nur gültig ist in Kategorien, deren Objekte Mengen (mit Zusatzstruktur) und deren Morphismen gewisse Abbildungen zwischen diesen Mengen sind, die wie üblich durch Hintereinanderausführung verknüpft werden usw. Für allgemeinere Kategorien kann man entweder den Einbettungssatz von Mitchell bemühen, der es erlaubt, jede (kleine) abelsche Kategorie als eine solche konkrete Kategorie von Moduln aufzufassen, oder aber statt Elementen Äquivalenzklassen von Morphismen mit dem entsprechenden Ziel verwenden; die Rechenregeln sind dieselben wie für Elemente.

Nutzt man Diagrammjagd zur Konstruktion von Abbildungen, so sind diese im Allgemeinen „natürlich“: Hat man zwei Exemplare des Diagramms, jedoch mit verschiedenen Objekten und Homomorphismen sowie einen Homomorphismus zwischen diesen Diagrammen (d.h. Homomorphismen von allen Objekten des einen Diagramms jeweils zum entsprechenden Objekt des zweiten Diagramms derart, dass alle entstehenden Maschen kommutativ sind), so werden auch die beiden konstruierten Abbildungen mit diesen Homomorphismen kommutieren.

Basierend auf einem Artikel in:

Wikipedia.de