Oktave (Mathematik)

𝕆

Die (reellen) Oktaven, auch Oktonionen oder Cayleyzahlen, sind eine Erweiterung der Quaternionen und besitzen das Mengensymbol $\mathbb {O}$ . Sie entstehen durch die Anwendung des Verdopplungsverfahrens aus den Quaternionen und bilden einen Alternativkörper. Damit liefern sie als Koordinatenbereich ein Beispiel für eine echte, das heißt nichtdesarguessche Moufangebene in der synthetischen Geometrie.

Geschichte

Die Oktonionen wurden im Jahr 1843 von John Thomas Graves in einem Brief an William Rowan Hamilton zum ersten Mal beschrieben. Unabhängig davon wurden sie 1845 von Arthur Cayley (als Erstem) veröffentlicht.

Multiplikationstabelle

Die Oktonionen sind eine 8-dimensionale Algebra über den reellen Zahlen. Eine mögliche Multiplikation ist – mit der Basis $(1,\mathrm {i} ,\mathrm {j} ,\mathrm {k} ,\mathrm {l} ,\mathrm {m} ,\mathrm {n} ,\mathrm {o} )$ – wie folgt gegeben:

${\begin{matrix}\mathrm {i} ^{2}=\mathrm {j} ^{2}=\mathrm {k} ^{2}=\mathrm {l} ^{2}=\mathrm {m} ^{2}=\mathrm {n} ^{2}=\mathrm {o} ^{2}=-1\\\mathrm {i} =\mathrm {jk} =\mathrm {lm} =\mathrm {on} =-\mathrm {kj} =-\mathrm {ml} =-\mathrm {no} \\\mathrm {j} =\mathrm {ki} =\mathrm {ln} =\mathrm {mo} =-\mathrm {ik} =-\mathrm {nl} =-\mathrm {om} \\\mathrm {k} =\mathrm {ij} =\mathrm {lo} =\mathrm {nm} =-\mathrm {ji} =-\mathrm {ol} =-\mathrm {mn} \\\mathrm {l} =\mathrm {mi} =\mathrm {nj} =\mathrm {ok} =-\mathrm {im} =-\mathrm {jn} =-\mathrm {ko} \\\mathrm {m} =\mathrm {il} =\mathrm {oj} =\mathrm {kn} =-\mathrm {li} =-\mathrm {jo} =-\mathrm {nk} \\\mathrm {n} =\mathrm {jl} =\mathrm {io} =\mathrm {mk} =-\mathrm {lj} =-\mathrm {oi} =-\mathrm {km} \\\mathrm {o} =\mathrm {ni} =\mathrm {jm} =\mathrm {kl} =-\mathrm {in} =-\mathrm {mj} =-\mathrm {lk} \end{matrix}}$

Daraus errechnet sich das Produkt der Einheiten

$\mathrm {ijklmno} \,=\,-1$

Man kann die Elemente $(\mathrm {i,j,k,l,m,n,o} )$ an Stelle der reellen Zahlen auch zu einem anderen (kommutativen) Körper adjungieren – mit der angegebenen Multiplikationstabelle und als Zentrum. Man nennt das Ergebnis die Cayley-Algebra über (welche aber nicht für jedes ohne Nullteiler ist).

Mit der Notation der Einheits-Oktonionen in der Form

$\{e_{0},e_{1},e_{2},e_{3},e_{4},e_{5},e_{6},e_{7}\},$

wobei $e_{0}$ das skalare Element bezeichnet und mit der reellen Zahl 1 identifiziert werden kann, schreibt sich die Multiplikationsmatrix:

		$e_{j}$
	$e_{i}e_{j}$	$e_{0}$	$e_{1}$	$e_{2}$		$e_{4}$	$e_{5}$	$e_{6}$	$e_{7}$
$e_{i}$	$e_{0}$	$e_{0}$	$e_{1}$	$e_{2}$		$e_{4}$	$e_{5}$	$e_{6}$	$e_{7}$
	$e_{1}$	$e_{1}$	$-e_{0}$		$-e_{2}$	$e_{5}$	$-e_{4}$	$-e_{7}$	$e_{6}$
	$e_{2}$	$e_{2}$	$-e_{3}$	$-e_{0}$	$e_{1}$	$e_{6}$	$e_{7}$	$-e_{4}$	$-e_{5}$
			$e_{2}$	$-e_{1}$	$-e_{0}$	$e_{7}$	$-e_{6}$	$e_{5}$	$-e_{4}$
	$e_{4}$	$e_{4}$	$-e_{5}$	$-e_{6}$	$-e_{7}$	$-e_{0}$	$e_{1}$	$e_{2}$
	$e_{5}$	$e_{5}$	$e_{4}$	$-e_{7}$	$e_{6}$	$-e_{1}$	$-e_{0}$	$-e_{3}$	$e_{2}$
	$e_{6}$	$e_{6}$	$e_{7}$	$e_{4}$	$-e_{5}$	$-e_{2}$		$-e_{0}$	$-e_{1}$
	$e_{7}$	$e_{7}$	$-e_{6}$	$e_{5}$	$e_{4}$	$-e_{3}$	$-e_{2}$	$e_{1}$	$-e_{0}$

Bis auf die Elemente in der $e_{0}$ -Spalte und Reihe ist die Matrix schiefsymmetrisch. Die Multiplikation kann auch geschrieben werden:

$e_{i}e_{j}={\begin{cases}e_{j},&{\text{für }}i=0\\e_{i},&{\text{für }}j=0\\-\delta _{ij}e_{0}+\varepsilon _{ijk}e_{k},&{\text{sonst}}\end{cases}}$

mit $\delta _{ij}$ dem Kronecker-Delta und $\varepsilon _{ijk}$ dem vollständig antisymmetrischen Tensor mit dem Wert +1 für ijk = 123, 145, 176, 246, 257, 347, 365.

Das ist nicht die einzige Wahl der Multiplikationstabelle, es gibt 480 weitere Möglichkeiten, erzeugt durch Permutation der $e_{i}$ verbunden mit Vorzeichenwechseln, die aber alle auf isomorphe Algebren führen.

Cayley-Dickson-Konstruktion

Man kann Oktonionen als Paare (a,b) von Quaternionen auffassen und die Oktonionen-Multiplikation der Paare (a,b) und (c,d) über

$(a,b)(c,d)=(ac-d^{*}b,da+bc^{*}),$

definieren, wobei $a^{*}$ die Konjugation einer Quaternion ist.

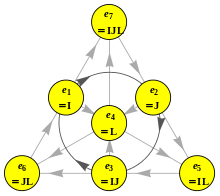
Multiplikation der Oktonionen mit Hilfe der Fano-Ebene

Fano-Ebene

Die Multiplikation der Oktonionen kann man in der Fano-Ebene darstellen (siehe Abbildung rechts). Die Punkte entsprechen den sieben Einheits-Oktonionen im Imaginärteil der Oktonionen (das heißt ohne $e_{0}=1$ ).

Durch die Pfeile ist eine Ordnung vorgegeben und Multiplikation zweier benachbarter Elemente auf einer Geraden resultiert im dritten Element auf der Geraden bei Fortschreiten in Pfeilrichtung (einige der Geraden sind in der Abbildung kreisförmig). Dabei wird zyklisch auf der Geraden vorangeschritten, das heißt man kann sich die Geraden als virtuell geschlossen vorstellen: (a, b, c)=(c, a, b)=(b, c, a). Bei Fortschreiten entgegen der Pfeilrichtung erhält man ein Minusvorzeichen. Zum Beispiel ergibt $e_{5}\cdot e_{3}=e_{6}$ . Wenn also (a,b,c) eine Gerade im Fano-Diagramm ist (mit Ordnung gemäß Pfeilrichtung), dann ist ab=c und ba=-c. Wie oben gilt $e_{0}=1$ und $e_{i}^{2}=-1$ für $i=1,\cdots ,7$ . Man überzeugt sich leicht anhand des Diagramms, dass die Multiplikation nicht-assoziativ ist.

Jede „Gerade“ im Fano-Diagramm bildet mit dem Einselement eine Unteralgebra der Oktonionen die isomorph zu den Quaternionen ist. Jeder Punkt bildet mit dem Einselement eine Unteralgebra die isomorph zu den komplexen Zahlen ist. Eine Gerade und ein Punkt außerhalb der Geraden erzeugen bereits das ganze Diagramm (also zwei beliebige imaginäre Einheits-Oktonionen $e_{i}$ , $e_{j}$ , die mit $e_{i}\cdot e_{j}$ eine Gerade bilden, sowie ein zusätzliches imaginäres Einheits-Oktonion e_k ).

Eigenschaften

Die Oktonionen sind eine Divisionsalgebra mit Einselement.

Sie bilden keinen Schiefkörper (und damit auch keinen Körper), denn sie verletzen das

Assoziativgesetz der Multiplikation: $a \cdot ( b \cdot c ) = ( a \cdot b ) \cdot c$ .

Es gilt jedoch für alle Oktaven a und b:

$a \cdot ( a \cdot b ) = ( a \cdot a ) \cdot b$ und $a \cdot ( b \cdot b ) = ( a \cdot b ) \cdot b$ .

Diese Eigenschaft wird Alternativität genannt und kann als abgeschwächte Form der Assoziativität aufgefasst werden (eine aus zwei beliebigen Oktonionen gebildete Unteralgebra ist assoziativ). Die Oktonionen bilden einen Alternativkörper.

Aus der Alternativität folgt die Beziehung

$a\cdot (b\cdot a)=(a\cdot b)\cdot a$ .

Diese Beziehung wird auch Flexibilitätsgesetz genannt.

Die Oktonionen erfüllen außerdem die Moufang-Identitäten

$[a \cdot (b \cdot a)] \cdot c = a \cdot [b \cdot (a \cdot c)]$

und

$(a \cdot b) \cdot (c \cdot a) = a \cdot [(b \cdot c) \cdot a]$

Anwendung des Verdopplungsverfahrens auf die Oktaven liefert die Sedenionen. Sie sind allerdings nicht mehr Nullteiler-frei (und auch nicht mehr alternativ). Im Rahmen des Verdopplungsverfahrens verlieren die betrachteten Algebren ausgehend von den reellen Zahlen zunehmend wichtige Eigenschaften, zuerst die Ordnungseigenschaft bei den komplexen Zahlen, dann die Kommutativität bei den Quaternionen und die Assoziativität bei den Oktonionen. Alle vier zusammen bilden die einzigen über den reellen Zahlen endlichdimensionalen, normierten Divisionsalgebren mit Einselement (Satz von Hurwitz).

Die Automorphismengruppe der Oktonionen ist die kleinste exzeptionelle einfache Liegruppe $G_{2}$ . Sie ist von der Dimension 14 und kann als Untergruppe von $SO(7)$ aufgefasst werden, die in ihrer 8-dimensionalen reellen Spinor-Darstellung einen beliebigen vorgegebenen Vektor fest lässt. Sie hat zwei fundamentale Darstellungen von 14 Dimensionen (die Adjungierte Darstellung) und 7 Dimensionen (diese ist gerade durch ihre Operationen auf dem siebendimensionalen Imaginärteil der Oktonionen – aufgefasst als Vektorraum über den reellen Zahlen – gegeben).

Darstellungen

Jede Oktave kann dargestellt werden…

… als 8er-Tupel von reellen Zahlen: $(r_{1},r_{2},\dotsc ,r_{8})$

… als 4er-Tupel von komplexen Zahlen: $(c_{1},c_{2},c_{3},c_{4})$

… als geordnetes Paar von Quaternionen: (h_1,h_2)

Der Körper der reellen Zahlen $\mathbb {R}$ kann als Unterstruktur von $\mathbb {O}$ betrachtet werden:

Für alle Zahlen aus $\mathbb {R}$ gilt: entspricht $(r, 0, \dotsc, 0)$

Der Körper der komplexen Zahlen $\mathbb {C}$ kann als Unterstruktur von $\mathbb {O}$ betrachtet werden:

Für alle Zahlen aus $\mathbb {C}$ gilt: entspricht (c,0,0,0)

Der Schiefkörper der Quaternionen $\mathbb H$ kann als Unterstruktur von $\mathbb {O}$ betrachtet werden:

Für alle Zahlen aus $\mathbb H$ gilt: entspricht (h, 0)

Für die Oktaven sind Addition und Multiplikation so definiert, dass sie abwärtskompatibel sind, das heißt…

… für alle reellen Zahlen und gilt:

$r+s=(r,0,\dotsc ,0)+(s,0,\dotsc ,0)$

$r \cdot s = (r, 0, \dotsc, 0) \cdot (s, 0, \dotsc,0)$

… für alle komplexen Zahlen und gilt:

$c\cdot d=(c,0,0,0)\cdot (d,0,0,0)$

… für alle Quaternionen und

gilt:

$h\cdot i=(h,0)\cdot (i,0)$

Konjugation, Norm, Inverse

Die Konjugierte eines Oktonions

$x=x_{0}\,e_{0}+x_{1}\,e_{1}+x_{2}\,e_{2}+x_{3}\,e_{3}+x_{4}\,e_{4}+x_{5}\,e_{5}+x_{6}\,e_{6}+x_{7}\,e_{7}$

wird definiert als:

$x^{*}=x_{0}\,e_{0}-x_{1}\,e_{1}-x_{2}\,e_{2}-x_{3}\,e_{3}-x_{4}\,e_{4}-x_{5}\,e_{5}-x_{6}\,e_{6}-x_{7}\,e_{7}.$

Konjugation ist eine Involution und es gilt

${(x\cdot y)}^{*}=y^{*}\cdot x^{*}$

Der Skalarteil des Oktonions ist gegeben durch:

${\frac {x+x^{*}}{2}}=x_{0}\,e_{0}$

und der Rest (Imaginärteil, entsprechend einem siebendimensionalen Untervektorraum) durch

${\frac {x-x^{*}}{2}}=x_{1}\,e_{1}+x_{2}\,e_{2}+x_{3}\,e_{3}+x_{4}\,e_{4}+x_{5}\,e_{5}+x_{6}\,e_{6}+x_{7}\,e_{7}.$

Die Konjugation erfüllt:

$x^{*}=-{\frac {1}{6}}(x+(e_{1}x)e_{1}+(e_{2}x)e_{2}+(e_{3}x)e_{3}+(e_{4}x)e_{4}+(e_{5}x)e_{5}+(e_{6}x)e_{6}+(e_{7}x)e_{7}).$

Das Produkt eines Oktonions mit seinem Konjugierten

$x^{*}x=x_{0}^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}+x_{5}^{2}+x_{6}^{2}+x_{7}^{2}.$

liefert eine reelle Zahl größer oder gleich Null und kann für die Definition einer Norm benutzt werden, die mit der üblichen euklidischen Norm in der Vektorraum-Darstellung der Oktonionen übereinstimmt:

$\|x\|={\sqrt {x^{*}x}}.$

Das inverse Element eines nicht-verschwindenden Oktonions kann damit so geschrieben werden:

$x^{-1}={\frac {x^{*}}{\|x\|^{2}}}.$

Es gilt $x^{-1}\cdot x=x\cdot x^{-1}=1$

Für das Produkt zweier Oktonionen gilt:

$\|xy\|=\|x\|\|y\|$

Das heißt, die Oktonionen bilden wie die reellen Zahlen, die komplexen Zahlen und die Quaternionen eine Kompositionsalgebra.

Anwendungen

Mittels der Cayley-Algebren lassen sich exzeptionelle Jordan-Algebren konstruieren und mittels Räumen von Derivationen auf solchen Jordan-Algebren können exzeptionelle Lie-Algebren angegeben werden.

Oktonionen können auch zur Konstruktion der fastkomplexen Struktur auf der 6-Sphäre benutzt werden.

In der Physik könnten Oktaven zur Beschreibung einer achtdimensionalen Supersymmetrie dienen. Damit ergäben sich auch mögliche Anwendungen in Zusammenhang mit der Stringtheorie und der M-Theorie, da beide auf der Supersymmetrie aufbauen.

Schon 1973 gab es Versuche, über die Untergruppen SU (3) und SU (2) x SU (2) der Automorphismengruppe der Oktonionen $G_{2}$ Teile des Standardmodells (Quarks) mit Oktonionen darzustellen (Feza Gürsey). Die grundlegende Gruppenstruktur der Wechselwirkungen des Standardmodells ist SU(3) x SU (2) x U (1) (kurz 1-2-3-Symmetrie). Die Gruppe SU (3) ergibt sich in der Automorphismengruppe $G_{2}$ der imaginären Oktonionen, indem man einen der imaginären Einheits-Oktonionen fest lässt. Ab Mitte der 2010er Jahre gab es Versuche der Physikerin Cohl Furey, weitere Elemente des Standardmodells aus der Oktonionenalgebra zu erhalten. Sie geht vom Tensorprodukt der vier Divisionsalgebren $\mathbb {R} \otimes \mathbb {C} \otimes \mathbb {H} \otimes \mathbb {O}$ aus und betrachtet Teilchen als Ideale darin. Die Raum-Zeit-Symmetrien (Lorentzgruppe) sind im $\mathbb {C} \otimes \mathbb {H}$ Teil der Quaternionen, die Gruppenstruktur des Standardmodells im $\mathbb {C} \otimes \mathbb {O}$ Teil der Oktonionen. 2018 implementierte sie darin die volle 1-2-3-Symmetriegruppe des Standardmodells mit einer Generation von Elementarteilchen. Es entspricht einer Version der GUT mit Eichgruppe SU (5) von Howard Georgi und Sheldon Glashow, allerdings mit einer möglichen Erklärung für die Unterbindung des Protonzerfalls. Sie fand auch eine Implementierung der ungebrochenen Symmetrien SU (3) und U (1) des Standardmodells mit drei Generationen.

Siehe auch

Hyperkomplexe Zahlen:

Quaternion

Basierend auf einem Artikel in:

Wikipedia.de