Automorphismus

In der Mathematik ist ein Automorphismus (von griechisch αὐτός autos „selbst“ und griechisch μορφή morphē „Gestalt“, „Form“) ein Isomorphismus eines mathematischen Objekts auf sich selbst.

Von Symmetrien zu Automorphismen

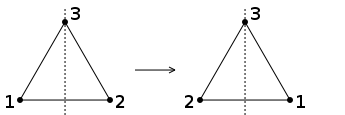
Ein gleichseitiges Dreieck hat drei Symmetrieachsen:

Equilateral triangle axes of symmetry.svg

Außerdem verfügt es über eine dreizählige Drehsymmetrie. Um die Symmetrieeigenschaft mathematisch zu fassen, betrachtet man die zugehörigen Symmetrieabbildungen. Zu jeder Symmetrieachse gehört die Spiegelung an der Achse:

Equilateral triangle vertical axis of symmetry.svg

Die Ziffern dienen nur dazu, die Abbildung zu beschreiben, es ist zweimal dasselbe Dreieck. Symmetrieabbildungen können nacheinander ausgeführt werden. Im folgenden Beispiel ist die Hintereinanderausführung zweier Spiegelungen eine Drehung um 120°:

Equilateral triangle composition of symmetries.svg

Führt man zweimal dieselbe Spiegelung nacheinander aus, erhält man insgesamt die Abbildung, die nichts verändert, die identische Abbildung. Wenn die Hintereinanderausführung zweier Symmetrieabbildungen wieder eine Symmetrieabbildung sein soll, muss man also die identische Abbildung zulassen. Eine Figur ist unsymmetrisch, wenn sie nur diese eine, triviale Symmetrieabbildung zulässt. Die Gesamtheit der Symmetrieabbildungen bildet eine Gruppe, die Symmetriegruppe.

In der Mathematik betrachtet man häufig Objekte, die aus einer Grundmenge und einer Zusatzstruktur bestehen, und in der Regel gibt es eine kanonische Konstruktion, die aus der Zusatzstruktur auf und einer Bijektion $f:G\to H$ eine Struktur $S_{f}$ auf erzeugt. Insbesondere ist das für Bijektionen $G\to G$ möglich.

Auf das Symmetriebeispiel übertragen entspricht der Ebene und dem Dreieck. Für eine Kongruenzabbildung $f:G\to G$ ist $S_{f}$ das Bilddreieck. Symmetrieabbildungen zeichnen sich durch $S=S_{f}$ aus. Im abstrakten Kontext nennt man Bijektionen $f:G\to G$ , die $S=S_{f}$ erfüllen, Automorphismen von (G,S) . Diese Definition deckt die meisten Fälle ab, seien es Graphen, topologische Räume oder algebraische Strukturen wie Vektorräume.

Werden die Zusatzstrukturen komplizierter, kann die harmlos erscheinende Bedingung $S=S_{f}$ Probleme bereiten: Definiert man differenzierbare Mannigfaltigkeiten als Grundmengen mit Topologie und einem Atlas , erhält man unter Umständen unter einem Homöomorphismus einen kompatiblen, aber nicht identischen Atlas $A_{f}$ . Würde man aber in der Definition einen maximalen Atlas fordern, wäre $A=A_{f}$ für ein solches .

Die Kategorientheorie löst dieses und andere Probleme dadurch, dass sie eine bereits vorhandene Definition für strukturkompatible Abbildungen voraussetzt (Morphismen; es muss sich nicht um tatsächliche Abbildungen handeln). Darauf aufbauend ersetzt sie die Forderung der Bijektivität (die im abstrakten Kontext nicht mehr zur Verfügung steht) durch die Existenz eines inversen Morphismus.

Definition

Algebraische Strukturen

Sei (A,(f_i)) eine algebraische Struktur, also eine Menge zusammen mit einer (meist endlichen) Anzahl an Verknüpfungen (f_i) . Eine solche algebraische Struktur könnte beispielsweise ein Vektorraum $(A, (+, \cdot))$ , eine Gruppe (A, *) oder ein Ring (A, ( +, *)) sein. Dann versteht man in der Algebra unter einem Automorphismus $\phi \colon A \to A$ eine bijektive Abbildung der Menge auf sich selbst, die ein Homomorphismus ist, das heißt, es gilt

$\phi \left(f_{i}(a_{1},\ldots ,a_{{\sigma _{i}}})\right)=f_{i}(\phi (a_{1}),\ldots ,\phi (a_{{\sigma _{i}}}))$

für alle $a_{1},\ldots ,a_{{\sigma _{i}}}\in A$ . Die Umkehrfunktion $\phi ^{{-1}}:A\to A$ ist dann ebenfalls ein Homomorphismus.

Kategorientheorie

Sei ein Objekt. Ein Morphismus $f\colon X\to X$ wird Automorphismus genannt, wenn es einen Morphismus $g\colon X\to X$ mit

$f\circ g=\operatorname {id}_{X}$ und $g\circ f=\operatorname {id}_{X}$

gibt, also ein beidseitiges Inverses besitzt.

Ein Automorphismus ist damit dasselbe wie

ein Isomorphismus, dessen Quelle und Ziel gleich sind, und
ein invertierbarer Endomorphismus.

Für Kategorien von algebraischen Strukturen (und den zugehörigen Homomorphismen) ist die Definition äquivalent zu der im vorherigen Abschnitt.

Automorphismengruppe

Wenn die Automorphismen eines Objekts eine Menge bilden, bilden sie mit der Verkettung als Verknüpfung eine Gruppe, die mit ${\mathrm {Aut}}(X)$ bezeichnet wird.
Ist eine Gruppe, nennt man einen Homomorphismus $G\to {\mathrm {Aut}}(X)$ eine Gruppenoperation von auf .
Ist $F:C\to D$ ein kovarianter Funktor und ein Objekt von , so induziert einen Gruppenhomomorphismus ${\mathrm {Aut}}(X)\to {\mathrm {Aut}}(F(X))$ . (Für kontravariante Funktoren muss man noch mit der Inversion $f\mapsto f^{{-1}}$ verketten.) Ist eine Gruppenoperation von auf gegeben, so erhält man auf diesem Wege eine Operation von auf .

Spezielle Strukturen

Graphen

Allgemeines

Ein Automorphismus eines Graphen G=(V,E) mit Knotenmenge und Kantenmenge ist eine bijektive Abbildung $\phi :V\to V$ , so dass $\{v_{1},v_{2}\}\in E\iff \{\phi (v_{1}),\phi (v_{2})\}\in E$ für alle $v_{1},v_{2}\in V$ gilt.

Ein Automorphismus eines Graphen induziert einen Automorphismus des Komplementgraphen.

Der Satz von Frucht besagt, dass zu jeder Gruppe $\Gamma$ ein Graph existiert, so dass ${\mathrm {Aut}}(G)$ isomorph zu $\Gamma$ ist.

Beispiel

Sei $V=\{1,2,3,4\}$ und $E=\{\{1,2\},\{3,4\}\}$ :

Automorphismen von G=(V,E) sind Permutationen von , so dass die Anwendung der Permutation auf das Diagramm wieder eine Veranschaulichung desselben Graphen ergibt. Beispiel: Die Permutation ${\begin{pmatrix}1&2&3&4\\4&3&1&2\end{pmatrix}}$ ist ein Automorphismus, weil die Kanten nach wie vor zwischen 1 und 2 sowie zwischen 3 und 4 verlaufen:

Die Permutation ${\begin{pmatrix}1&2&3&4\\1&3&2&4\end{pmatrix}}$ ist kein Automorphismus, weil die Kanten im neuen Bild $\{1,3\}$ und $\{2,4\}$ sind:

Die Automorphismengruppe des Graphen ist isomorph zur Diedergruppe der Ordnung , sein Komplement ist ein 4-Zyklus.

Vektorräume

Ein Automorphismus eines Vektorraums ist eine bijektive lineare Abbildung $V\to V$ .

Für endlichdimensionale Vektorräume sind Automorphismen genau diejenigen linearen Abbildungen $V\to V$ , deren Abbildungsmatrix bezüglich einer beliebigen Basis regulär ist. Die Automorphismengruppe wird häufig als GL(V) notiert.

Gruppen

Allgemeines

Ein Automorphismus einer Gruppe $(G,\circ )$ ist ein bijektiver Gruppenhomomorphismus dieser Gruppe auf sich selbst, das heißt eine bijektive Abbildung $\phi \colon G\to G$ mit $\phi(g \circ h)=\phi(g) \circ \phi(h)$ für alle $g,h\in G$ .

Unter Automorphismen bleiben alle strukturellen Eigenschaften der Gruppenelemente sowie diesbezügliche Konstruktionen erhalten. So erhält jeder Automorphismus die Ordnung der Elemente (d.h. $ord(\phi(g))=ord(g)$ für alle $g\in G$ ), induziert einen Automorphismus des Zentrums und bildet Erzeugendensysteme auf Erzeugendensysteme ab.

Innere Automorphismen

Ist eine Gruppe und $h\in G$ fest, dann ist $i_{h}:G\to G$ , $i_{h}(g)=hgh^{{-1}}$ ein Automorphismus von , genannt Konjugation mit . Automorphismen, die auf diesem Weg entstehen, heißen innere Automorphismen. Automorphismen, die keine inneren Automorphismen sind, heißen äußere Automorphismen. Weil $h\mapsto i_{h}$ ein Homomorphismus $G\to {\mathrm {Aut}}(G)$ ist und $i_{h}$ genau dann der triviale Automorphismus ist, wenn im Zentrum von liegt, ist die Menge ${\mathrm {Inn}}(G)$ aller inneren Automorphismen nach dem Homomorphiesatz eine zu G/Z(G) isomorphe Untergruppe von ${\mathrm {Aut}}(G)$ . Sie ist sogar ein Normalteiler in ${\mathrm {Aut}}(G)$ , und die Faktorgruppe ${\mathrm {Aut}}(G)/{\mathrm {Inn}}(G)$ wird mit ${\mathrm {Out}}(G)$ bezeichnet. Sie heißt Gruppe der äußeren Automorphismen. Die Einschränkung auf das Zentrum liefert einen Homomorphismus ${\mathrm {Out}}(G)\to {\mathrm {Aut}}(Z(G))$ .

Für abelsche Gruppen sind alle inneren Homomorphismen trivial, und ${\mathrm {Aut}}(G)={\mathrm {Out}}(G)$ .

Für eine Untergruppe $H\subseteq G$ erhält man durch Einschränkung der inneren Automorphismen einen injektiven Homomorphismus $N_{G}(H)/Z_{G}(H)\to {\mathrm {Aut}}(H)$ . Siehe Normalisator und Zentralisator.

Beispiele

Die bijektive Abbildung $G\to G$ , $g\mapsto g^{{-1}}$ , ist genau dann ein Homomorphismus und damit ein Automorphismus, wenn abelsch ist.
Die Gruppe $\mathbb {Z}$ hat genau einen nichttrivialen Automorphismus, nämlich $x\mapsto -x$ . Das folgt daraus, dass ein Automorphismus ein Erzeugendensystem auf ein Erzeugendensystem abbildet.
Die Automorphismengruppe der kleinschen Vierergruppe ist isomorph zur symmetrischen Gruppe $S_{3}$ .
Die Automorphismengruppe der Gruppe $(\mathbb{Q} ,+)$ ist $\Q^*$ (durch Multiplikation), die Automorphismengruppe der Gruppe $(\mathbb{Q} ^{*},\cdot )$ ist überabzählbar.
Der Automorphismus $A\mapsto (A^{T})^{{-1}}$ von ${\mathrm {GL}}_{n}(\mathbb{R} )$ ist kein innerer Automorphismus, weil seine Einschränkung auf das Zentrum, die Untergruppe der Skalarmatrizen, nicht trivial ist.

Körper

Ein Automorphismus eines Körpers ist eine bijektive Abbildung $\phi :K\to K$ , die $\phi (x+y)=\phi (x)+\phi (y)$ und $\phi (xy)=\phi (x)\phi (y)$ für alle $x,y\in K$ erfüllt. Ist L/K eine Körpererweiterung, dann nennt man diejenigen Automorphismen $\phi$ von , die $\phi (x)=x$ für alle $x\in K$ erfüllen, die -Automorphismen von . Sie bilden eine Gruppe, notiert ${\mathrm {Aut}}_{K}(L)$ oder $\mathrm{Aut}(L/K)$ . Ein Automorphismus von ist genau dann ein -Automorphismus, wenn er eine -lineare Abbildung ist.

Die Konjugation $a+bi\mapsto a-bi$ für $a,b\in\R$ ist ein $\mathbb {R}$ -Automorphismus des Körpers $\mathbb {C}$ der komplexen Zahlen.
Die Abbildung $a+b{\sqrt 2}\mapsto a-b{\sqrt 2}$ ist für $a,b\in \mathbb{Q}$ der einzige nichttriviale Automorphismus von $\mathbb{Q} [{\sqrt 2}]$ .
Der Körper der rationalen Zahlen $\mathbb {Q}$ und der Körper der reellen Zahlen $\mathbb {R}$ besitzen keine nichttrivialen Automorphismen. Man bezeichnet sie deshalb auch als starr. Wie das Beispiel $\mathbb{Q} [{\sqrt 2}]$ zeigt, überträgt sich Starrheit nicht auf Unter-, Ober-, Zwischenkörper. Dass $\mathbb {Q}$ starr ist, erkennt man daran, dass sich jede rationale Zahl als algebraischer Ausdruck in darstellen lässt, wobei die als neutrales Element der Multiplikation unter Automorphismen erhalten bleiben muss. Jeder Automorphismus auf $\mathbb {R}$ muss entsprechend jede rationale Zahl auf sich selbst abbilden. Da er zudem dieOrdnung erhält, müssen sogar alle reellen Zahlen Fixpunkt sein.
Ist ein endlicher oder allgemeiner perfekter Körper der Charakteristik , dann ist $x\mapsto x^{p}$ ein Automorphismus von , der Frobeniusautomorphismus.
Ist ein Körper und $G\subseteq {\mathrm {Aut}}(L)$ eine Untermenge, dann ist $K=\{x\in L\;\mid \;\forall \phi \in G:\phi (x)=x\}$ ein Unterkörper von , genannt der Fixkörper von . Ist eine endliche Untergruppe, so ist ist eine Galoiserweiterung vom Grad . Die Galoistheorie stellt weitere Verbindungen zwischen Körpererweiterungen und Automorphismengruppen her.

Algebren

Für Algebren kann man wie bei Gruppen innere Automorphismen als Konjugation mit einer Einheit definieren. Innere Automorphismen sind trivial auf dem Zentrum, und der Satz von Skolem-Noether besagt, dass für eine halbeinfache Algebra auch die Umkehrung gilt.

Funktionentheorie

In der Funktionentheorie sind die Morphismen die holomorphen Funktionen und die Automorphismen die konformen Selbstabbildungen. Die Automorphismengruppe bspw. der offenen Einheitskreisscheibe $\mathbb {E}$ ist gegeben durch:

$\operatorname {Aut}({\mathbb {E}})=\left\{\varphi :{\mathbb {E}}\to {\mathbb {E}}\;\mid \;\varphi (z)=\lambda {\frac {z-a}{{\bar {a}}z-1}}:\lambda \in \partial {\mathbb {E}},a\in {\mathbb {E}}\right\}$