
Diedergruppe

In der Gruppentheorie
ist die Diedergruppe
als semidirektes
Produkt
erklärt (siehe unten) und
enthält daher genau
Elemente. Für
ist diese Gruppe
isomorph zur Isometriegruppe
eines regelmäßigen
Polygons in der Ebene. Sie ist dann nicht-abelsch und enthält
Drehungen
und
Achsenspiegelungen.
Ihr Name leitet sich vom Wort Dieder
(Silbentrennung: Di-eder, Aussprache [diˈeːdər])
(griechisch:
Zweiflächner) für regelmäßige
-Ecke
ab. Diese Gruppen treten häufig in der Geometrie
und Gruppentheorie auf, werden von zwei Spiegelungen (Elementen der Ordnung
)
erzeugt und sind damit die einfachsten Beispiele von Coxeter-Gruppen.
Bezeichnungen
Es gibt für Diedergruppen zwei abweichende Bezeichnungen. In der Geometrie
schreibt man üblicherweise ,
um den Zusammenhang mit dem regelmäßigen
-Eck
zu unterstreichen. In der Gruppentheorie schreibt man oft auch
,
um stattdessen die Ordnung
hervorzuheben. Diese Zweideutigkeit lässt sich jedoch leicht durch eine
erläuternde Ergänzung beheben. In diesem Artikel steht
für die Diedergruppe mit
Elementen.
Definition
Die Diedergruppe
kann für
als die Isometriegruppe eines regelmäßigen
-Ecks
in der Ebene definiert werden. Diese besteht aus
Drehungen und
Spiegelungen, hat also insgesamt
Elemente. Die Isometrien bezeichnet man auch als Symmetrietransformationen. Als
Verknüpfung
der Gruppe
dient die Hintereinanderausführung
von Symmetrietransformationen.
In den Fällen
und
führt die geometrische Definition jedoch zu anderen Gruppen. Daher ist hier die
algebraische Definition über das semidirekte
Produkt
vorzuziehen (dabei ist in dem semidirekten Produkt die Operation von
auf
durch Inversion gegeben). Diese algebraische Definition gilt für alle
.
Beispiele
Ein Beispiel ist die Diedergruppe
der Kongruenzabbildungen eines gleichseitigen
Dreiecks auf sich, die isomorph zur symmetrischen Gruppe
ist.
ist entsprechend die Symmetriegruppe des Quadrats unter Spiegelungen und
Drehungen.
ist isomorph zur Kleinschen
Vierergruppe und ist die Symmetriegruppe (bestehend nur aus den beiden
Spiegelungen, der Drehung um 180° und der Identität) von den vier Ecken eines
Quadrats, bei dem nur die rechte und linke Seite eingezeichnet sind (also zwei
Zweiecke).
ist die Symmetriegruppe eines Zweiecks.
ist auch die Symmetriegruppe eines nicht gleichseitigen
Rechtecks oder einer nicht gleichwinkligen
Raute.
ist auch die Symmetriegruppe eines gleichschenkligen
Dreiecks, das nicht gleichseitig ist.
Die folgende Grafik illustriert die Diedergruppe
anhand der Drehungen und Spiegelungen eines Stoppschildes: Die erste Zeile zeigt
die acht Drehungen, die zweite Zeile die acht Spiegelungen.
Matrix-Darstellung
Wir betrachten ein ebenes regelmäßiges -Eck.
Seinen Mittelpunkt wählen wir als Nullpunkt
eines Koordinatensystems, irgendeine seiner
Symmetrieachsen als
-Achse
und die Normale dazu (in üblicher Orientierung, sodass sich ein Rechtssystem
ergibt) als
-Achse.
Die Diedergruppe
lässt sich dann leicht als Matrixgruppe darstellen. Hierzu sei
die Drehung um
um den Winkel
und
die Spiegelung an der Geraden durch
,
die im Winkel
gegenüber der positiven
-Achse
geneigt ist. Als Matrizen schreiben sich diese Transformationen dann so:
Hierbei fallen folgende Relationen auf:
und
. Daher können wir uns auf
beschränken.
, die Drehung um den Winkel
, ist die Identität.
ist die Drehung um den Winkel
und es gilt
für alle
.
ist die Spiegelung an der
-Achse und es gilt
für alle
.
Wenn
ungerade ist, dann verläuft jede der
Spiegelachsen durch einen Eckpunkt und den Mittelpunkt der gegenüberliegenden
Seite. Für gerades
gibt es hingegen zwei Arten von Spiegelachsen, durch zwei gegenüberliegende
Eckpunkte oder durch zwei gegenüberliegende Seitenmittelpunkte.
In dieser Darstellung schreiben sich zum Beispiel die acht Elemente der
Diedergruppe
wie folgt:
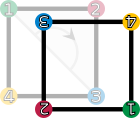
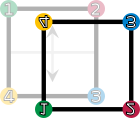
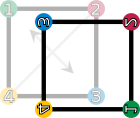
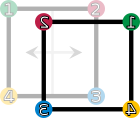
Diese Drehungen und Spiegelungen lassen sich bildlich wie folgt darstellen:

 |
 |
 |
 |
 |
 |
 |
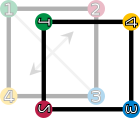 |
| Drehungen und Spiegelungen eines Quadrates. Die vier Ecken sind nummeriert und eingefärbt, um die Transformation bildlich darzustellen. | |||
Permutations-Darstellung
Betrachten wir zunächst als Beispiel die Diedergruppe .
Diese operiert durch Symmetrietransformationen auf einem Quadrat wie in der
vorangehenden Grafik gezeigt. Betrachtet man die Aktion der Diedergruppe
auf den Eckpunkten
,
erhält man eine treue Darstellung in die symmetrische Gruppe
,
also einen injektiven Gruppenhomomorphismus
.
Genauer gesagt wirken die Transformationen auf den Ecken als folgende
Permutationen:
Ganz allgemein definiert die Operation der Diedergruppe
auf den Eckpunkten
eine treue Darstellung
.
In obiger Notation erhält man zum Beispiel die Permutation
In Zyklenschreibweise
ist dies die zyklische
Permutation, die
auf
abbildet,
auf
und so weiter, bis schließlich
auf
abgebildet wird. Die weiteren Drehungen erhält man hieraus mittels der Relation
für alle
.
Für die Spiegelung an der Symmetrieachse durch
erhält man entsprechend in Zyklenschreibweise
mit der Gaußschen Ganzteilfunktion
(die jeder reellen Zahl
die größte ganze Zahl zuordnet, die nicht größer als
ist). Die weiteren Spiegelungen erhält man hieraus mittels der Relation
für alle
(mit
).
Erzeuger und Relationen
Alle
Drehungen werden von
erzeugt. Diese bilden eine zyklische Untergruppe der Ordnung
und demnach von Index
.
Man erhält die gesamte Gruppe durch Hinzufügen einer beliebigen Spiegelung, zum
Beispiel
,
und so die Präsentation
wobei
das neutrale Element der Gruppe ist.

Die Verkettung von zwei Spiegelungen ist eine Drehung. Ist der Winkel
zwischen den beiden Spiegelachsen ,
so ist diese Verkettung eine Drehung um den Winkel
.
Das bedeutet, dass die Diedergruppe
von zwei benachbarten Spiegelungen, zum Beispiel
und
,
erzeugt wird. Man erhält so die Präsentation
Dies ist der einfachste Fall einer Coxeter-Gruppe.
Für alle Indizes
und
gilt außerdem:
Dabei werden die Indizes jeweils modulo
betrachtet (
und
).
Anwendungen
Geometrie
Diedergruppen sind die einfachsten Beispiele von Spiegelungsgruppen. Diese
spielen in der klassischen Geometrie
eine wichtige Rolle, zum Beispiel bei der Klassifikation der regulären Polyeder.
In Dimension
entsprechen hier Diedergruppen den regulären Polygonen.
Codierung
Die durch obige Permutationen definierte Zahlenverknüpfung wird bei Prüfsummenverfahren als Alternative zu diversen modulo-basierten Verfahren angewendet. Zum Beispiel besaßen die deutschen Banknoten Dieder-Prüfsummen.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 19.02. 2022
