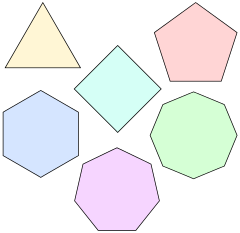
Regelmäßiges Polygon
|
|
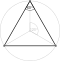
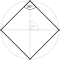
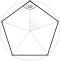
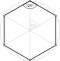
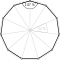
Ein regelmäßiges Polygon, reguläres Polygon, regelmäßiges Vieleck, reguläres Vieleck oder Isogon (von griechisch ἴσος, gleich und γωνία, Winkel) ist in der Geometrie ein ebenes Polygon, das sowohl gleichseitig, als auch gleichwinklig ist. Bei einem regelmäßigen Polygon sind demnach alle Seiten gleich lang und alle Innenwinkel gleich groß. Die Ecken eines regelmäßigen Polygons liegen alle auf einem gemeinsamen Kreis, wobei benachbarte Ecken unter dem gleichen Mittelpunktswinkel erscheinen.
Regelmäßige Polygone können einfach oder überschlagen
sein. Einfache regelmäßige Polygone sind stets konvex.
Überschlagene regelmäßige Polygone werden als reguläre Sternpolygone bezeichnet.
Die Symmetriegruppe
eines regelmäßigen -Ecks
ist die Diedergruppe
bestehend aus genau
Drehungen
und
Spiegelungen.
Alle Kenngrößen regelmäßiger Polygone, wie die Länge der Diagonalen, der
Umfang oder der Flächeninhalt, können mit Hilfe trigonometrischer
Funktionen angegeben werden. Nicht alle regelmäßigen Polygone sind jedoch
mit
Zirkel und Lineal konstruierbar. Regelmäßige Polygone werden unter anderem
bei der Näherung der Kreiszahl
,
für Parkettierungen, in der
Architektur und als Münzform
verwendet.
Definition
Ein Polygon mit den
Seiten
und den Innenwinkeln
heißt regelmäßig, wenn
und
gilt. In einem regelmäßigen Polygon sind demnach alle Seiten zueinander kongruent und alle Winkel gleich groß.
Klassifikation
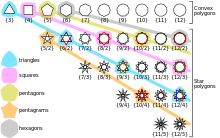
Man unterscheidet einfache und überschlagene regelmäßige Polygone. Alle
einfachen regelmäßigen Polygone mit
Ecken sind zueinander ähnlich
und werden in der kombinatorischen
Geometrie mit dem Schläfli-Symbol
bezeichnet. Um degenerierte Fälle auszuschließen, wird in der Regel
angenommen. Die ersten einfachen regelmäßigen Polygone sind:
- das gleichseitige
Dreieck
,
- das Quadrat
,
- das regelmäßige Fünfeck
und
- das regelmäßige Sechseck
.
Überschlagene regelmäßige Polygone werden reguläre Sternpolygone genannt und
weisen eine größere Vielfalt an Formen auf. Sie werden mit dem Schläfli-Symbol
bezeichnet, wobei
die Windungszahl des Polygons
um seinen Mittelpunkt angibt. Die Windungszahl muss dabei teilerfremd zu
sein, ansonsten entartet das Polygon. Die ersten regelmäßigen Sternpolygone
sind
- der Fünfstern
,
- die Siebensterne
und
sowie
- der Achtstern
.
Die Anzahl der verschiedenen Typen regelmäßiger Polygone mit
Ecken ist demnach
,
wobei
die eulersche
Phi-Funktion ist. Sind
und
nicht teilerfremd, werden mit dem Schläfli-Symbol
Sterne
bezeichnet, die aus mehreren regelmäßigen Polygonen zusammengesetzt sind.
Beispiele sind das Hexagramm
und das Oktagramm
.
Kenngrößen
Winkel
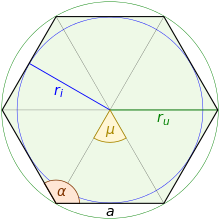
Die Ecken eines regelmäßigen Polygons liegen konzyklisch auf
einem gemeinsamen Kreis. Ein regelmäßiges Polygon ist damit ein
Sehnenvieleck und besitzt
so einen Umkreis mit Umkreisradius
.
Zudem liegen die Ecken gleichabständig auf dem Kreis, das heißt nebeneinander
liegende Ecken erscheinen unter dem gleichen Mittelpunktswinkel
(Zentriwinkel)
.
Damit ist ein regelmäßiges Polygon auch ein Tangentenvieleck
mit einem Inkreis mit Inkreisradius
.
Der Inkreis berührt die Polygonseiten dabei in den Seitenmittelpunkten. Der
Inkreismittelpunkt stimmt mit dem Umkreismittelpunkt überein und wird der
Mittelpunkt des Polygons genannt. Nachdem die Winkelsumme
in einem einfachen
-Eck
stets
ergibt, messen in einem einfachen regelmäßigen Polygon alle Innenwinkel
.
Da sich an den Ecken eines Polygons Innen- und Außenwinkel
zu
ergänzen, sind in einem einfachen regelmäßigen Polygon auch alle Außenwinkel
gleich groß und messen jeweils
.
Für die Winkel in regelmäßigen Polygonen ergeben sich beispielsweise folgende Werte:
| Polygon | Mittelpunktswinkel
|
Innenwinkel
|
Außenwinkel
| |||
|---|---|---|---|---|---|---|
| Gradmaß | Bogenmaß | Gradmaß | Bogenmaß | Gradmaß | Bogenmaß | |
| Dreieck | ||||||
| Viereck | ||||||
| Fünfeck | ||||||
| Sechseck | ||||||
| Achteck | ||||||
| Zehneck | ||||||
| Zwölfeck | ||||||
Längen
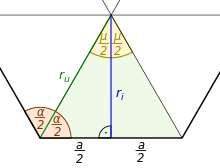
Die wichtigsten Kenngrößen einfacher regelmäßiger Polygone können mit Hilfe
des Bestimmungsdreiecks, das von dem Mittelpunkt und zwei benachbarten Ecken des
Polygons gebildet wird, ermittelt werden. Das Bestimmungsdreieck ist
gleichschenklig
mit dem Spitzenwinkel ,
den Basiswinkeln
,
den Schenkeln
,
der Basis
und der Höhe
.
Wird das Bestimmungsdreieck entlang der Höhe (dem Apothema)
in zwei rechtwinklige
Dreiecke unterteilt, ergeben sich mit dem oben angegebenen
Mittelpunktswinkel und den trigonometrischen
Funktionen (Sinus
und Kosinus, Tangens
und Kotangens sowie Sekans
und Kosekans) die folgenden Beziehungen zwischen der Seitenlänge
,
dem Umkreisradius
und dem Inkreisradius
:
Für manche Werte von
lassen sich explizite Formeln für die Funktionswerte der trigonometrischen
Funktionen (siehe Formelsammlung
Trigonometrie) und damit für die Längen in einfachen regelmäßigen Polygonen
angeben, zum Beispiel:
| Polygon | Seitenlänge
|
Umkreisradius
|
Inkreisradius
| |||
|---|---|---|---|---|---|---|
| Umkreisradius | Inkreisradius | Seitenlänge | Inkreisradius | Seitenlänge | Umkreisradius | |
| Dreieck | ||||||
| Viereck | ||||||
| Fünfeck | ||||||
| Sechseck | ||||||
| Achteck | ||||||
| Zehneck | ||||||
| Zwölfeck | ||||||
Umfang und Flächeninhalt
Der Umfang
eines einfachen regelmäßigen Polygons ist das -fache
der Seitenlänge und
damit
.
Der Flächeninhalt
eines einfachen regelmäßigen Polygons ist entsprechend das -fache
der Fläche
des Bestimmungsdreiecks:
.
Die letzte Gleichung folgt dabei aus der Doppelwinkelformel. Damit ergeben sich beispielsweise die folgenden expliziten Formeln für den Umfang und den Flächeninhalt einfacher regelmäßiger Polygone:
| Polygon | Seitenlänge
|
Umkreisradius
|
Inkreisradius
| |||
|---|---|---|---|---|---|---|
| Umfang | Flächeninhalt | Umfang | Flächeninhalt | Umfang | Flächeninhalt | |
| Dreieck | ||||||
| Viereck | ||||||
| Fünfeck | ||||||
| Sechseck | ||||||
| Achteck | ||||||
| Zehneck | ||||||
| Zwölfeck | ||||||
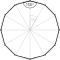
Diagonalen
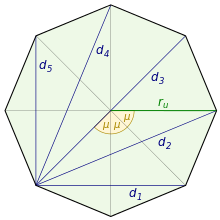
Von jeder Ecke eines regelmäßigen -Ecks
gehen
Diagonalen
bis
aus. Die Länge der Diagonalen kann wiederum mit Hilfe des Bestimmungsdreiecks,
das von dem Mittelpunkt des Polygons und den beiden Endpunkten der Diagonale
gebildet wird, ermittelt werden. Das Bestimmungsdreieck der
-ten
Diagonale,
,
ist wieder gleichschenklig und hat die Schenkel
,
die Basis
und den Spitzenwinkel
.
Damit ergibt sich für die Länge der
-ten
Diagonale
.
Für die Längen der Diagonalen in einem einfachen regelmäßigen Polygon gilt die Identität
.
Ist die Eckenzahl des Polygons gerade, sind daher
Diagonalen unterschiedlich lang; ist die Eckenzahl ungerade, gibt es
verschieden lange Diagonalen. Bei gegebener Seitenlänge
ergeben sich beispielsweise die folgenden expliziten Formeln für die Längen der
Diagonalen einfacher regelmäßiger Polygone:
| Polygon | Diagonalen | ||||
|---|---|---|---|---|---|
| Diagonale |
Diagonale |
Diagonale |
Diagonale |
Diagonale | |
| Viereck | |||||
| Fünfeck | |||||
| Sechseck | |||||
| Achteck | |||||
| Zehneck | |||||
| Zwölfeck | |||||
Eigenschaften
Symmetrien
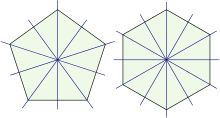
Die Symmetriegruppe
eines regelmäßigen -Ecks
ist die Diedergruppe
.
Die Diedergruppe weist die Ordnung
auf und besteht aus
Rotationen der zyklischen Gruppe
und
Spiegelungen an den Symmetrieachsen durch den Mittelpunkt des Polygons.
Ist
gerade, dann verläuft die eine Hälfte der Symmetrieachsen durch zwei
gegenüberliegende Ecken und die andere Hälfte durch zwei Mittelpunkte
gegenüberliegender Seiten. Ist
ungerade, dann verlaufen alle Symmetrieachsen durch eine Ecke und den
Mittelpunkt der gegenüberliegenden Seite.
Jedes regelmäßige Polygon mit gerader Eckenzahl ist auch punktsymmetrisch bezüglich seines Mittelpunkts.
Zerlegungen
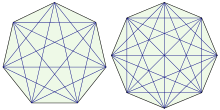
Die Gesamtzahl aller Diagonalen in einem regelmäßigen -Eck
ergibt sich zu
(Folge A000096 in OEIS),
da von jeder der
Ecken
Diagonalen ausgehen und bei dieser Zählung alle Diagonalen doppelt gezählt
werden. Bei einem einfachen regelmäßigen Polygon mit gerader Eckenzahl verlaufen
alle Diagonalen durch den Mittelpunkt des Polygons. Bei ungerader Eckenzahl wird
durch die Diagonalen im Inneren ein verkleinerte Kopie des Polygons gebildet.
Die Anzahl der Schnittpunkte der Diagonalen im Inneren eines einfachen
regelmäßigen
-Ecks
ergibt die Folge
(Folge A006561 in OEIS).
Die Anzahl der Teilpolygone, die durch eine vollständige Zerlegung eines
einfachen regelmäßigen -Ecks
entlang der Diagonalen entsteht, ergibt die Folge
(Folge A007678 in OEIS).
Die Anzahl der Möglichkeiten, ein einfaches regelmäßiges -Eck
überschneidungsfrei entlang der Diagonalen in Teilpolygone zu zerteilen, wird
durch die kleinen Schröder-Zahlen
angegeben. Sollen diese Teilpolygone ausschließlich Dreiecke sein, wird die
Anzahl der Möglichkeiten durch die Catalan-Zahlen
angegeben. Allgemeiner werden auch Zerlegungen regelmäßiger Polygone untersucht,
bei denen nicht nur die Diagonalen verwendet werden dürfen, zum Beispiel die Zerlegung
in flächengleiche Dreiecke.
Abstände
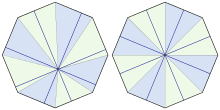
Nach dem Satz
von Viviani ist die Summe
der senkrechten
Abstände von einem beliebigen Punkt
im Inneren eines einfachen regelmäßigen Polygons zu den Polygonseiten gleich der
Summe der Abstände vom Mittelpunkt zu den Seiten und damit gleich
.
Betrachtet man nämlich die Dreiecke, die von dem Punkt
und jeweils zwei benachbarten Eckpunkten gebildet werden, dann ist die Summe der
Flächeninhalte dieser Dreiecke gleich dem gesamten Flächeninhalt des Polygons,
also
.
Die Aussage ergibt sich dann durch Dividieren beider Seiten der Gleichung
durch .
Weitere Identitäten in regelmäßigen Polygonen sind:
- Die Summe der Abstände von den Eckpunkten zu einer beliebigen Umkreistangente ist
.
- Die Summe der Abstandsquadrate von den Eckpunkten zu einem beliebigen
Punkt auf dem Umkreis ist
.
- Die Summe der Abstandsquadrate von den Seitenmitten zu einem beliebigen
Punkt auf dem Umkreis ist
.
Das Produkt der Abstände von einem Eckpunkt zu allen anderen Eckpunkten ergibt sich in einem regelmäßigen Polygon zu
.
Maximalität

Regelmäßige Polygone maximieren nach dem Satz von Zenodoros den Flächeninhalt im Vergleich zu anderen Polygonen in folgender Weise:
- Von allen
-Ecken mit gleichem Umfang hat das regelmäßige
-Eck den größten Flächeninhalt.
- Von allen in einen gegebenen Kreis einbeschriebenen
-Ecken hat das regelmäßige
-Eck den größten Flächeninhalt.
- In jeder endlichen Menge regelmäßiger Polygone mit gleichem Umfang hat dasjenige mit den meisten Ecken den größten Flächeninhalt.
Andererseits gilt aber auch die isoperimetrische Ungleichung:
- Ein Kreis hat einen größeren Flächeninhalt als jedes regelmäßige Polygon mit gleichem Umfang.
Konstruktion
Zirkel und Lineal
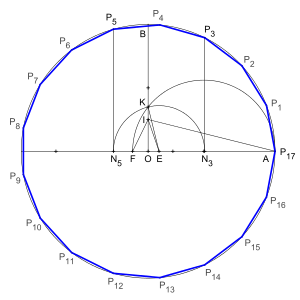
Die Frage, welche regelmäßigen -Ecke
unter ausschließlicher Verwendung von Zirkel
und Lineal konstruiert werden können, wurde bereits in der Antike
untersucht, aber erst im 19. Jahrhundert von Carl Friedrich
Gauß und Pierre Wantzel abschließend beantwortet. Demnach ist ein regelmäßiges Polygon genau
dann mit Zirkel und Lineal konstruierbar, wenn die Zahl seiner Seiten von der
Form
ist, wobei
und
paarweise voneinander verschiedene fermatsche
Primzahlen sind. Das kleinste nicht konstruierbare regelmäßige Polygon ist
damit das regelmäßige Siebeneck.
Lässt man zur Konstruktion zusätzlich ein Hilfsmittel zur Dreiteilung eines
Winkels zu, so sind alle regelmäßigen Polygone mit Seitenzahlen der Form
konstruierbar, wobei
und
verschiedene Pierpont-Primzahlen
größer als drei sind. Auf diese Weise sind beispielsweise auch das regelmäßige
Siebeneck,
das regelmäßige Neuneck> und das regelmäßige
Dreizehneck
konstruierbar, nicht jedoch das regelmäßige Elfeck.
Konkrete Konstruktionsvorschriften für regelmäßige Polygone zu finden gestaltet
sich jedoch mit wachsender Eckenzahl schnell als sehr aufwändig. Es gibt solche
Konstruktionsvorschriften aber unter anderem für das 17-Eck, das 257-Eck und das 65537-Eck.
Koordinaten
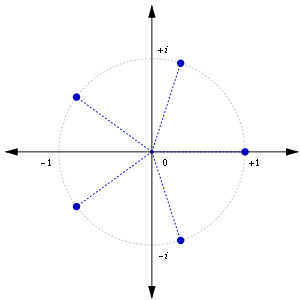
Zur Berechnung der Eckpunkte eines regelmäßigen -Ecks
können die komplexen
Lösungen der Kreisteilungsgleichung
verwendet werden. Die Polarkoordinaten
des
-ten
Eckpunkts eines regelmäßigen
-Ecks
mit der Windungszahl
(bei einfachen Polygonen ist
),
dem Koordinatenursprung
als Mittelpunkt, dem Umkreisradius
und dem Drehwinkel
haben so die einfache Form
.
Für ,
und
entsprechen diese Eckpunkte gerade den
-ten
Einheitswurzeln in der
komplexen
Zahlenebene. In einem kartesischen
Koordinatensystem lauten die Koordinaten
des
-ten
Eckpunkts entsprechend
.
Algorithmus
In Pseudocode kann ein
regelmäßiges Polygon mit
Ecken, der Windungszahl
,
dem Umkreisradius
und dem Drehwinkel
somit wie folgt dargestellt werden:
function regpoly(n,m,r,t)
for k = 1 to n // Schleife über die Seiten bzw. Ecken
w = 2 * pi * m/n; // Mittelpunktswinkel
x1 = r * cos(k*w+t); // Koordinaten (x1,y1) des ersten Eckpunkts
y1 = r * sin(k*w+t);
x2 = r * cos((k+1)*w+t); // Koordinaten (x2,y2) des zweiten Eckpunkts
y2 = r * sin((k+1)*w+t);
line(x1,y1,x2,y2) // Linie von (x1,y1) nach (x2,y2)
end
Asymptotik
Kreis als Grenzform

Für wachsende Seitenzahl
nähert sich die Form eines einfachen regelmäßigen
-Ecks
bei konstantem Inkreis- oder Umkreisradius immer mehr einem Kreis an. Das
Verhältnis von Umfang und Inkreis- oder Umkreisradius strebt dabei gegen den
Grenzwert
.
Das Verhältnis von Flächeninhalt und dem Quadrat des
Inkreis- oder des Umkreisradius strebt für wachsendes
entsprechend gegen den Grenzwert
.
| Seitenzahl | Umkreisradius
|
Inkreisradius
| ||||||
|---|---|---|---|---|---|---|---|---|
| Seitenlänge | Inkreisradius | Umfang | Flächeninhalt | Seitenlänge | Umkreisradius | Umfang | Flächeninhalt | |
| 3 | 1,732050808 | 0,500000000 | 5,196152423 | 1,299038106 | 3,464101615 | 2,000000000 | 10,39230485 | 5,196152423 |
| 4 | 1,414213562 | 0,707106781 | 5,656854249 | 2,000000000 | 2,000000000 | 1,414213562 | 8,000000000 | 4,000000000 |
| 5 | 1,175570505 | 0,809016994 | 5,877852523 | 2,377641291 | 1,453085056 | 1,236067978 | 7,265425280 | 3,632712640 |
| 6 | 1,000000000 | 0,866025404 | 6,000000000 | 2,598076211 | 1,154700538 | 1,154700538 | 6,928203230 | 3,464101615 |
| 7 | 0,867767478 | 0,900968868 | 6,074372348 | 2,736410189 | 0,963149238 | 1,109916264 | 6,742044663 | 3,371022332 |
| 8 | 0,765366865 | 0,923879533 | 6,122934918 | 2,828427125 | 0,828427125 | 1,082392200 | 6,627416998 | 3,313708499 |
| 9 | 0,684040287 | 0,939692621 | 6,156362580 | 2,892544244 | 0,727940469 | 1,064177772 | 6,551464217 | 3,275732108 |
| 10 | 0,618033989 | 0,951056516 | 6,180339888 | 2,938926261 | 0,649839392 | 1,051462224 | 6,498393925 | 3,249196962 |
| 100 | 0,062821518 | 0,999506560 | 6,282151816 | 3,139525976 | 0,062852532 | 1,000493683 | 6,285253209 | 3,142626604 |
| 1000 | 0,006283175 | 0,999995065 | 6,283174972 | 3,141571983 | 0,006283206 | 1,000004935 | 6,283205978 | 3,141602989 |
| 10000 | 0,000628319 | 0,999999951 | 6,283185204 | 3,141592447 | 0,000628319 | 1,000000049 | 6,283185514 | 3,141592757 |
| 100000 | 0,000062832 | 0,999999999 | 6,283185306 | 3,141592652 | 0,000062832 | 1,000000000 | 6,283185309 | 3,141592655 |
Apeirogon als Grenzform
 |
 | |
|
Regelmäßige Parkettierungen der hyperbolischen
Ebene durch Apeirogone | ||
Wird bei wachsender Seitenzahl
stattdessen die Seitenlänge konstant gehalten, nähert sich die Form eines
einfachen regelmäßigen
-Ecks
einer degenerierten geometrischen
Figur an, die Apeirogon
(von griechisch
ἄπειρον,
das Unbeschränkte) genannt wird und mit dem Schläfli-Symbol
bezeichnet wird.
Ein Apeirogon kann als eine Aneinanderreihung unendlich vieler gleich langer
Linienstücke der Form
- ..
 ...
...
visualisiert werden oder auch als Kreis mit einem unendlich großen Radius angesehen werden. Die Innenwinkel eines Apeirogons sind gestreckte Winkel und messen daher
.
Im hyperbolischen Raum ist ein Apeirogon jedoch nicht mehr degeneriert und besitzt eine Reihe interessanter Eigenschaften. So lässt sich beispielsweise die hyperbolische Ebene durch Apeirogone auf verschiedene Weisen regelmäßig parkettieren.
Schachtelungen
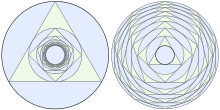
Wird in einen Einheitskreis ein regelmäßiges Dreieck einbeschrieben, in dessen Inkreis dann ein regelmäßiges Viereck, in wiederum dessen Inkreis ein regelmäßiges Fünfeck, und so weiter, dann konvergiert die Folge der Inkreisradien gegen den Grenzwert
(Folge A085365 in OEIS),
der Kepler-Bouwkamp-Konstante oder polygon inscribing constant genannt wird. Analog konvergiert Folge der Umkreisradien, wenn um einen Einheitskreis abwechselnd regelmäßige Polygone mit wachsender Seitenzahl und deren Umkreise umbeschrieben werden, gegen den Grenzwert
(Folge A051762 in OEIS),
der als polygon circumscribing constant bekannt ist.
Das Produkt der beiden Konstanten ist 1.
Verwendung
Polygonalzahlen
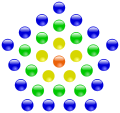 |
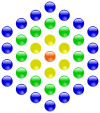 | |
|
Die vierte zentrierte Fünfeckszahl (31) und
Sechseckszahl (37) | ||
In der Zahlentheorie werden die Polygonalzahlen
und die zentrierten
Polygonalzahlen betrachtet, die dadurch entstehen, dass mit einer bestimmten
Zahl von Steinen regelmäßige Polygone gelegt werden. Nach dem fermatschen
Polygonalzahlensatz lässt sich jede Primzahl
als Summe von höchstens
solcher
-Eckszahlen
darstellen. Ein bekannter Spezialfall dieses Satzes ist der Vier-Quadrate-Satz
von Joseph Louis Lagrange. Die dreidimensionalen Verallgemeinerungen der
Polygonalzahlen heißen Pyramidalzahlen.
Näherung von π
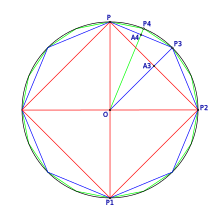
Archimedes setzte im 3.
Jahrhundert v. Chr. erstmals regelmäßige Polygone ein, um die Kreiszahl
mit Hilfe der Exhaustionsmethode
näherungsweise zu berechnen. Hierzu verwendete er eine Folge von Polygonen, die
einem Einheitskreis
mit Radius
ein- beziehungsweise umbeschrieben sind. Er begann dabei mit dem regelmäßigen
Sechseck und führte die Reihe mit dem Zwölfeck, dem 24-Eck, dem 48-Eck bis hin
zum 96-Eck fort. Auf diese Weise gewann er die Abschätzung
.
Im Mittelalter setzten chinesische und persische Wissenschaftler diese
Berechnungen mit dem 192-Eck und weiteren Polygonen fort. Ludolph van Ceulen
führte im 16. Jahrhundert Berechnungen bis zum regelmäßigen -Eck
durch und ermittelte so die Kreiszahl
bis auf 35 Stellen genau. Allgemein ergeben sich durch die Approximation eines
Kreises mit ein- und umschriebenen regelmäßigen
-Ecken
Abschätzungen von
der Form
.
Die trigonometrischen Terme lassen sich dabei mit Hilfe von Rekursionsformeln berechnen.
Parkettierungen
 |
 | |
|
Parkettierungen aus Dreiecken, Vierecken und
Sechsecken | ||
Regelmäßige Polygone können auch als Kacheln einer Parkettierung der Ebene verwendet werden. Wird nur ein regelmäßiges Polygon als Kachel zugelassen, wobei die Kacheln Kante an Kante angeordnet werden müssen, ergeben sich die drei platonischen Parkettierungen aus regelmäßigen Dreiecken, Vierecken und Sechsecken. Werden verschiedene regelmäßige Polygone als Kacheln zugelassen, wobei an den Ecken stets die gleiche Anordnung von Polygonen zusammenstoßen muss, erhält man die acht archimedischen Parkettierungen. Eine weitaus größere Vielfalt an Parkettierungen ergibt sich, wenn an den Ecken unterschiedliche Kombinationen von Polygonen zugelassen werden.
Polyeder
Im dreidimensionalen Raum bilden regelmäßige Polygone die Seitenflächen von regulären Polyedern. Wird nur ein regelmäßiges Polygon verwendet, wobei an den Ecken immer gleich viele Polygone zusammenstoßen müssen, erhält man die fünf platonischen Körper Tetraeder, Hexaeder, Oktaeder, Dodekaeder und Ikosaeder. Werden verschiedene regelmäßige Polygone als Seitenflächen zugelassen, wobei an den Ecken stets die gleiche Anordnung von Polygonen zusammenstoßen muss, ergeben sich die 13 archimedischen Körper sowie bestimmte Prismen und Antiprismen. Werden auch nichtuniforme Ecken zugelassen, erhält man die 92 Johnson-Körper. Mit manchen dieser Polyeder lässt sich auch der dreidimensionale Raum parkettieren. Es gibt auch Sternkörper, deren Seitenflächen regelmäßige Polygone sind, wie zum Beispiel das Sterntetraeder.
Vorkommen
Architektur

Regelmäßige Polygone werden in der Architektur häufig als Grundriss von Zentralbauten verwendet. Beispielsweise sind
- quadratisch: die ägyptischen Pyramiden, Vierungstürme im Kirchenbau
- fünfeckig: das Pentagon in Washington, die Festung Rosenberg in Kronach
- sechseckig: die Festung Saarlouis, das Fort Jefferson in Florida
- siebeneckig: das Kultur- und Kongresszentrum Liederhalle in Stuttgart, das Fürstliche Mausoleum in Stadthagen
- achteckig: der Felsendom in Jerusalem, das Castel del Monte in Apulien
- neuneckig: die Festungsstadt Palmanova, die Häuser der Andacht der Bahai
- zwölfeckig: der Torre del Oro in Sevilla, die Kirche La Vera Cruz in Segovia
- vierzehneckig: die Kirche Notre-Dame de l’Assomption in Rieux-Minervois
- sechzehneckig: der Zentralbau des Aachener Doms, die Stierkampfarena La Malagueta in Málaga
Numismatik

Münzen sind nicht immer kreisrund, sondern haben manchmal auch eine polygonale Form. Solche in der Numismatik als Klippen bezeichnete Münzen wurden früher als Notmünzen geprägt, sie finden sich gelegentlich aber auch als Kurs- oder Gedenkmünzen. Beispiele für im Umlauf befindliche Klippen in Form eines regelmäßigen Polygons sind:
- quadratisch: die 50-Cent-Münze der niederländischen Antillen
- sechseckig: die indische 20-Paise-Münze
- siebeneckig: die britischen 20- und 50-Pence-Münzen
- achteckig: die chilenischen Ein- und Fünf-Peso-Münzen
- elfeckig: die indische Zwei-Rupien-Münze
- zwölfeckig: die australische 50-Cent-Münze
Moderne Klippen haben dabei häufig die Form eines Reuleaux-Polygons mit nach außen gekrümmten Seiten, damit sie auch von Münzautomaten erkannt werden können.
Natur

Regelmäßige polygonale Strukturen kommen auch in der Natur vor. Manche Atome können cyclische Verbindungen eingehen, wie zum Beispiel der Benzolring C6H6 in Form eines regelmäßigen Sechsecks. Auch in der Struktur von Kristallen treten regelmäßige Polygone auf, beispielsweise in kubischen oder hexagonalen Kristallsystemen. In der Biologie finden sich regelmäßige Polygone unter anderem bei Okrafrüchten (fünfeckig) und Bienenwaben (sechseckig).
Symbolik
Einige regelmäßige Polygone haben neben der geometrischen auch eine symbolische Bedeutung, zum Beispiel das Dreiecksymbol oder das Pentagramm. Verkehrszeichen, insbesondere Vorfahrtsschilder, haben häufig die Form eines regelmäßigen Polygons mit abgerundeten Ecken.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 28.06. 2022